Lesson 8 7 Coordinate Proof with Quadrilaterals Transparency

Lesson 8 -7 Coordinate Proof with Quadrilaterals

Transparency 8 -7 5 -Minute Check on Lesson 8 -6 ABCD is an isosceles trapezoid with median EF. 1. Find m D if m A= 110°. 70° 2. Find x if AD = 3 x² + 5 and BC = x² + 27. ± 4 3. Find y if AC = 9(2 y – 4) and BD = 10 y + 12. 4. Find EF if AB = 10 and CD = 32. B A E F D C 6 21 5. Find AB if AB = r + 18, CD = 6 r + 9 and EF = 4 r + 10. 25 6. Standardized Test Practice: Which statement is always true about trapezoid LMNO with bases of LM and NO? A LO // MN B LO MN C LM // NO D LM NO Click the mouse button or press the Space Bar to display the answers.

Objectives • Position and label quadrilaterals for use in coordinate proofs • Prove theorems using coordinate proofs

Vocabulary • Kite – quadrilateral with exactly two distinct pairs of adjacent congruent sides.

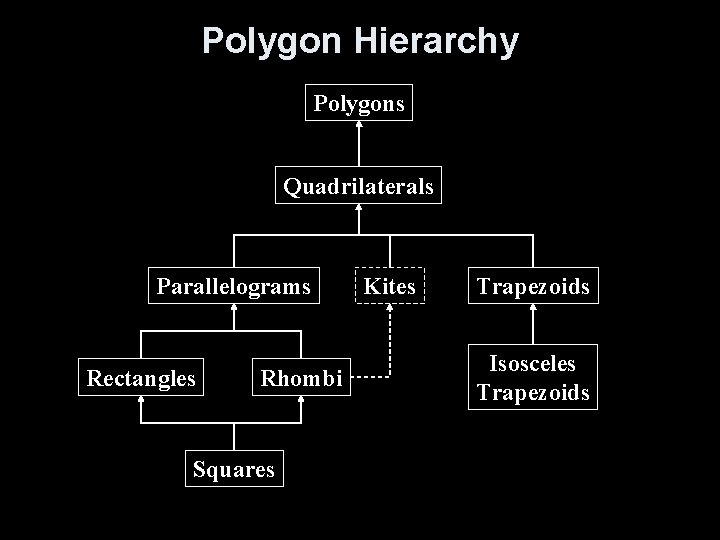
Polygon Hierarchy Polygons Quadrilaterals Parallelograms Rectangles Rhombi Squares Kites Trapezoids Isosceles Trapezoids

Name the missing coordinates for the isosceles trapezoid. y D(? , ? ) C(a-b, c) x A(0, 0) B(a, 0) The legs of an isosceles trapezoid are congruent and have opposite slopes. Point C is c units up and b units to the left of B. So, point D is c units up and b units to the right of A. Therefore, the x-coordinate of D is 0 + c, or c and the y-coordinate of D is 0 + b, or b. Answer: D (b, c)

Name the missing coordinates for the rhombus. Answer:

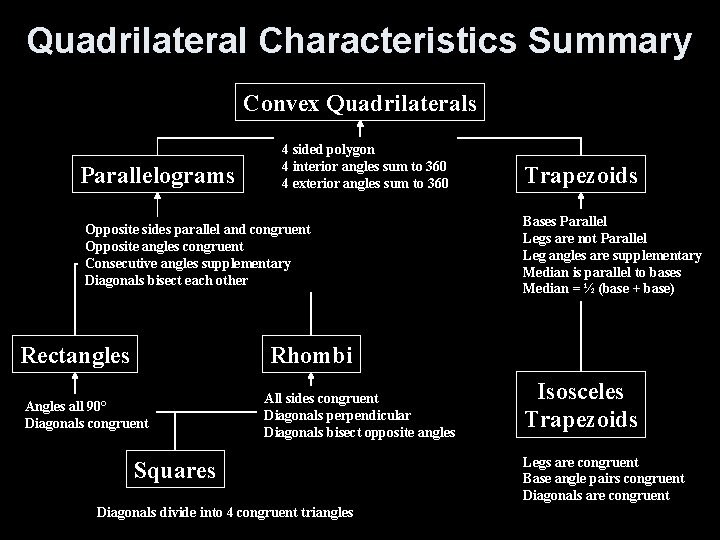
Quadrilateral Characteristics Summary Convex Quadrilaterals Parallelograms 4 sided polygon 4 interior angles sum to 360 4 exterior angles sum to 360 Opposite sides parallel and congruent Opposite angles congruent Consecutive angles supplementary Diagonals bisect each other Rectangles Trapezoids Bases Parallel Legs are not Parallel Leg angles are supplementary Median is parallel to bases Median = ½ (base + base) Rhombi Angles all 90° Diagonals congruent All sides congruent Diagonals perpendicular Diagonals bisect opposite angles Squares Diagonals divide into 4 congruent triangles Isosceles Trapezoids Legs are congruent Base angle pairs congruent Diagonals are congruent

Do you know your characteristics? • Extra Credit Assignment • Review Problems

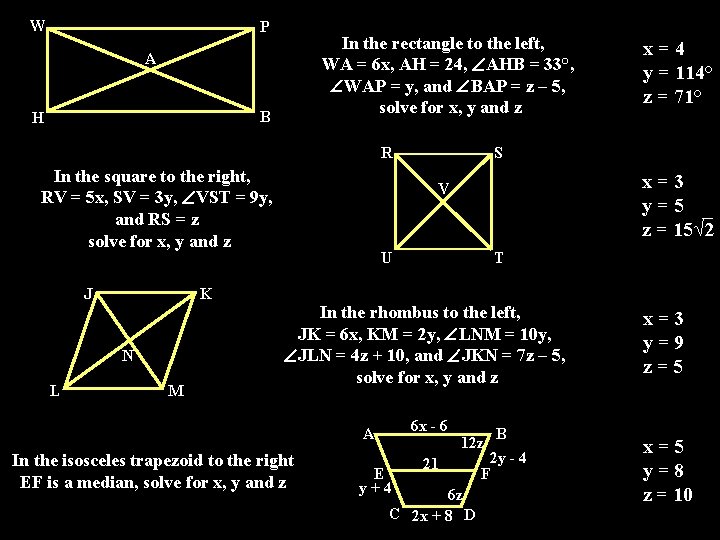
W P In the rectangle to the left, WA = 6 x, AH = 24, AHB = 33°, WAP = y, and BAP = z – 5, solve for x, y and z A B H R In the square to the right, RV = 5 x, SV = 3 y, VST = 9 y, and RS = z solve for x, y and z J S x=3 y=5 z = 15√ 2 V U T K N L x=4 y = 114° z = 71° M In the rhombus to the left, JK = 6 x, KM = 2 y, LNM = 10 y, JLN = 4 z + 10, and JKN = 7 z – 5, solve for x, y and z 6 x - 6 A In the isosceles trapezoid to the right EF is a median, solve for x, y and z E y+4 12 z 21 6 z C 2 x + 8 D B 2 y - 4 F x=3 y=9 z=5 x=5 y=8 z = 10

Summary & Homework • Summary: – Position a quadrilateral so that a vertex is at the origin and a least one side lies along an axis. • Homework: – pg 450 -451; 9, 11 -14, 28, 29, 31 -33