Lesson 8 4 The Binomial Theorem Objective to

Lesson 8. 4 – The Binomial Theorem Objective • to use the Binomial Theorem to calculate binomial coefficients • to use Pascal's Triangle to calculate binomial coefficients • to use binomial coefficients to write binomial expansions What if all I had today was what I was thankful for yesterday? Slides developed from material copyrighted by Houghton Mifflin Company 1

Homework 8. 4 Day 2 pg 604 1 -4, 5, 7, 9, 17, 18, 23, 29, 55, 56, 71 -74, 113 -16 2

Binomial Expansion (x + y)0 = 1 (x + y)1 = 1 x + 1 y (x + y)2 = 1 x 2 + 2 xy + 1 y 2 (x + y)3 = 1 x 3 + 3 x 2 y + 3 xy 2 + 1 y 3 (x + y)4 = 1 x 4 + 4 x 3 y + 6 x 2 y 2 + 4 xy 3 + 1 y 4 3

Pascal's Triangle The nth row of Pascal’s Triangle gives the coefficients of (x +

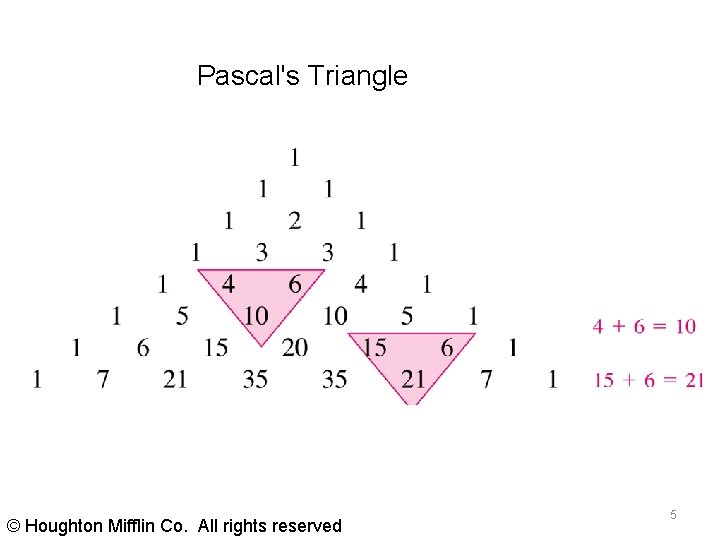
Pascal's Triangle © Houghton Mifflin Co. All rights reserved 5

List five general observations about the expansion of (x + y)n for various values of n. 1) In each expansion, there are n + 1 terms. 2) In each expansion, x and y have symmetrical roles. The powers of x decrease by 1 in successive terms, whereas the powers of y increase by 1. 3) The sum of the powers in each term is n. 4) The coefficients increase and then decrease in a symmetrical pattern. 5) If you add the coefficients from any row (n) the sum is 2 n 6

The Binomial Theorem states that in the expansion of (x + y)n = xn + nxn – 1 y +. . . + n. Crxn – ryr +. . . + nxyn – 1 + yn, Where n – ry r C x n r is the (r + 1)st term 7

n – r yr C x n r is the (r + 1)st term Note: ‘r’ is the exponent of the y term. It is always 1 less then the term number. For example: y 1 is in the 2 nd term y 2 is in the 3 rd term 8

Special Case If (x – y)n : just alternate signs between the terms, starting with positive. That’s all! + - + - 9

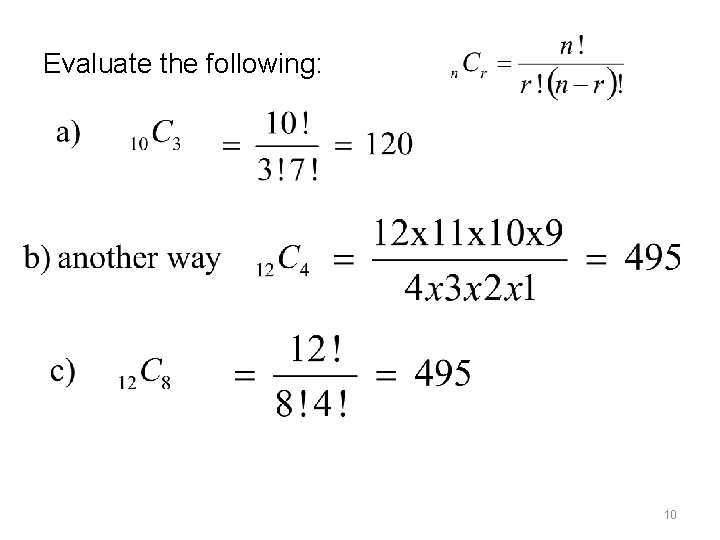
Evaluate the following: 10

For binomial coefficients: n. C r = n C n – r= n n. C 0 = n. C n = 1 (x + y)4 = 1 x 4 + 4 x 3 y + 6 x 2 y 2 + 4 xy 3 + 1 y 4 8 C 0 = 8 C 8 = ? 8 C 1 = 1 8 C 7 = ? 8 11