LESSON 8 3 Graphing Reciprocal Functions FiveMinute Check

LESSON 8– 3 Graphing Reciprocal Functions

Five-Minute Check (over Lesson 8– 2) TEKS Then/Now New Vocabulary Key Concept: Parent Function of Reciprocal Functions Example 1: Limitations on Domain Example 2: Determine Properties of Reciprocal Functions Key Concept: Transformations of Reciprocal Functions Example 3: Graph Transformations Example 4: Real-World Example: Write Equations

You graphed polynomial functions. • Determine properties of reciprocal functions. • Graph transformations of reciprocal functions.

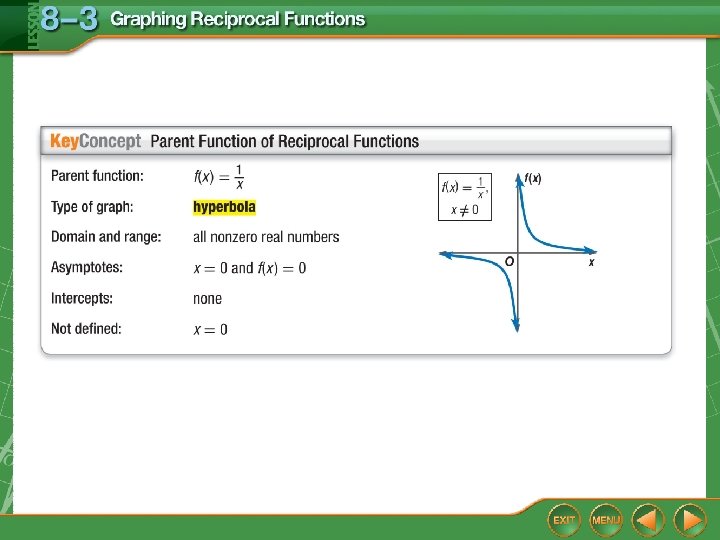
• reciprocal function • hyperbola

Limitations on Domain Determine the values of x for which is not defined. Factor the denominator of the expression. Answer: The function is undefined for x = – 8 and x = 3.

Determine the values of x for which is not defined. A. x = – 7, x = 4 B. x = – 14, x = 2 C. x = – 4, x = 7 D. x = – 2, x = 14

Determine Properties of Reciprocal Functions A. Identify the asymptotes, domain, and range of the function. Identify the x-values for which f(x) is undefined. x– 2 = 0 x= 2 f(x) is not defined when x = 2. So, there is an asymptote at x = 2.

Determine Properties of Reciprocal Functions From x = 2, as x-values decrease, f(x)-values approach 0, and as x-values increase, f(x)-values approach 0. So, there is an asymptote at f(x) = 0. Answer: There asymptotes at x = 2 and f(x) = 0. The domain is all real numbers not equal to 2 and the range is all real numbers not equal to 0.

Determine Properties of Reciprocal Functions B. Identify the asymptotes, domain, and range of the function. Identify the x-values for which f(x) is undefined. x+2 = 0 x = – 2 f(x) is not defined when x = – 2. So, there is an asymptote at x = – 2.

Determine Properties of Reciprocal Functions From x = – 2, as x-values decrease, f(x)-values approach 1, and as x-values increase, f(x)-values approach 1. So, there is an asymptote at f(x) = 1. Answer: There asymptotes at x = – 2 and f(x) = 1. The domain is all real numbers not equal to – 2 and the range is all real numbers not equal to 1.

A. Identify the asymptotes of the function. A. x = 3 and f(x) = 3 B. x = 0 and f(x) = – 3 C. x = – 3 and f(x) = – 3 D. x = – 3 and f(x) = 0

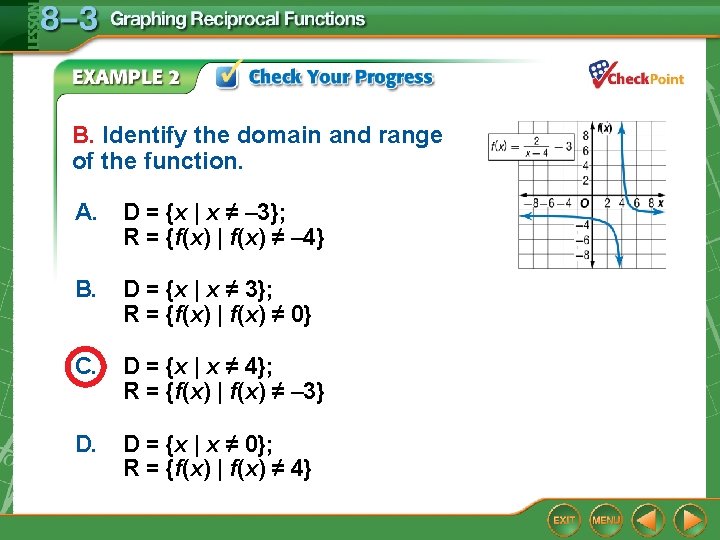
B. Identify the domain and range of the function. A. D = {x | x ≠ – 3}; R = {f(x) | f(x) ≠ – 4} B. D = {x | x ≠ 3}; R = {f(x) | f(x) ≠ 0} C. D = {x | x ≠ 4}; R = {f(x) | f(x) ≠ – 3} D. D = {x | x ≠ 0}; R = {f(x) | f(x) ≠ 4}

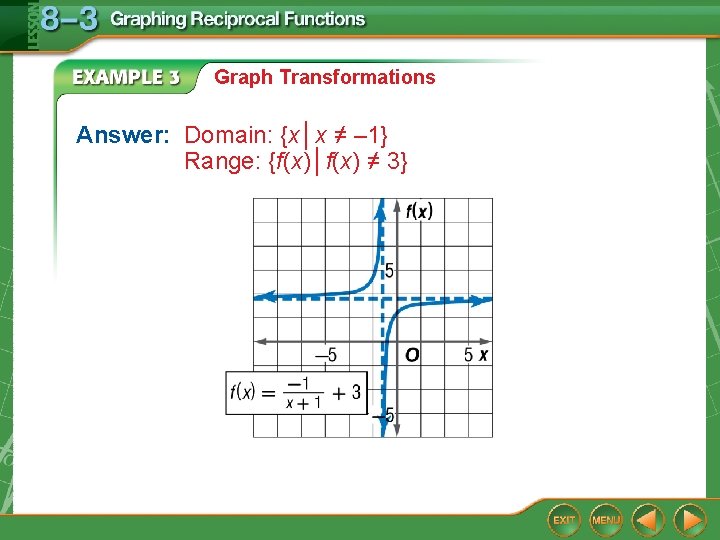
Graph Transformations A. Graph the function State the domain and range. This represents a transformation of the graph of a = – 1: h = – 1: k = 3: The graph is reflected across the x-axis. The graph is translated 1 unit left. There is an asymptote at x = – 1. The graph is translated 3 units up. There is an asymptote at f(x) = 3.

Graph Transformations Answer: Domain: {x│x ≠ – 1} Range: {f(x)│f(x) ≠ 3}

Graph Transformations B. Graph the function State the domain and range. This represents a transformation of the graph of a = – 4: The graph is stretched vertically and reflected across the x-axis. h = 2: The graph is translated 2 units right. There is an asymptote at x = 2.

Graph Transformations k = – 1: The graph is translated 1 unit down. There is an asymptote at f(x) = – 1. Answer: Domain: {x│x ≠ 2} Range: {f(x)│f(x) ≠ – 1}

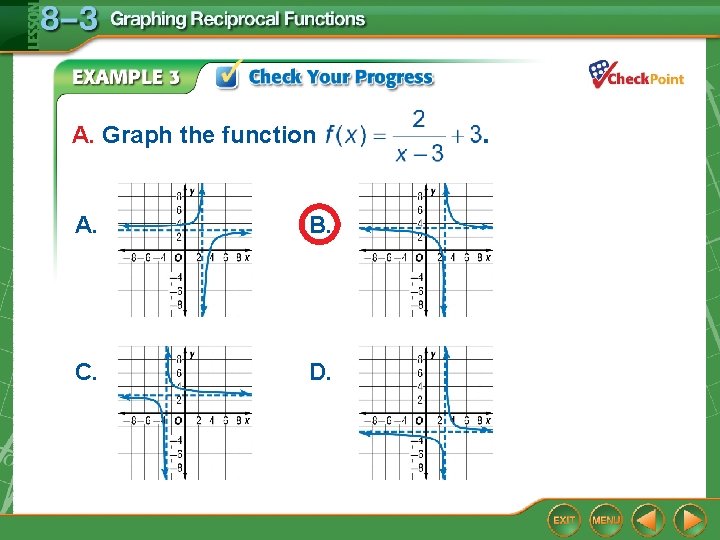
A. Graph the function A. B. C. D.

B. State the domain and range of A. Domain: {x│x ≠ – 1}; Range: {f(x)│f(x) ≠ – 2} B. Domain: {x│x ≠ 4}; Range: {f(x)│f(x) ≠ 2} C. Domain: {x│x ≠ 1}; Range: {f(x)│f(x) ≠ – 2} D. Domain: {x│x ≠ – 1}; Range: {f(x)│f(x) ≠ 2}

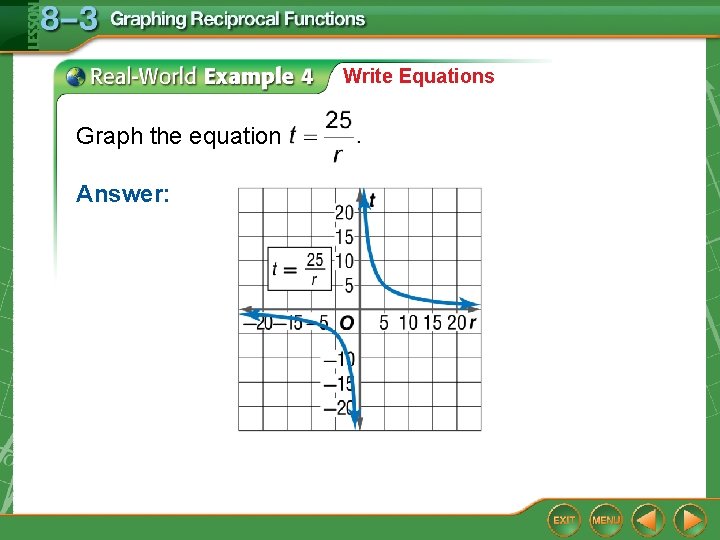
Write Equations A. COMMUTING A commuter train has a nonstop service from one city to another, a distance of about 25 miles. Write an equation to represent the travel time between these two cities as a function of rail speed. Then graph the equation. Solve the formula r t = d for t. rt = d Original equation. Divide each side by r. d = 25

Write Equations Graph the equation Answer:

Write Equations B. COMMUTING A commuter train has a nonstop service from one city to another, a distance of about 25 miles. Explain any limitations to the range and domain in this situation. Answer: The range and domain are limited to all real numbers greater than 0 because negative values do not make sense. There will be further restrictions to the domain because the train has minimum and maximum speeds at which it can travel.

A. TRAVEL A commuter bus has a nonstop service from one city to another, a distance of about 76 miles. Write an equation to represent the travel time between these two cities as a function of rail speed. A. B. C. D.

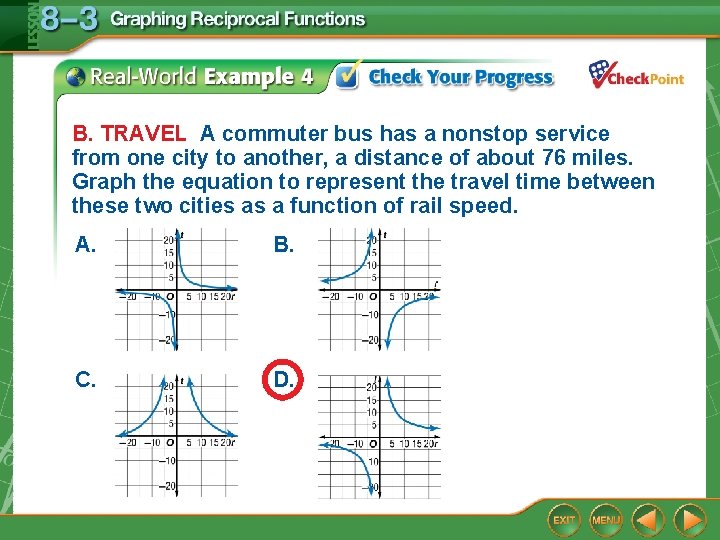
B. TRAVEL A commuter bus has a nonstop service from one city to another, a distance of about 76 miles. Graph the equation to represent the travel time between these two cities as a function of rail speed. A. B. C. D.

LESSON 8– 3 Graphing Reciprocal Functions