Lesson 72 Using the properties of logarithms Log




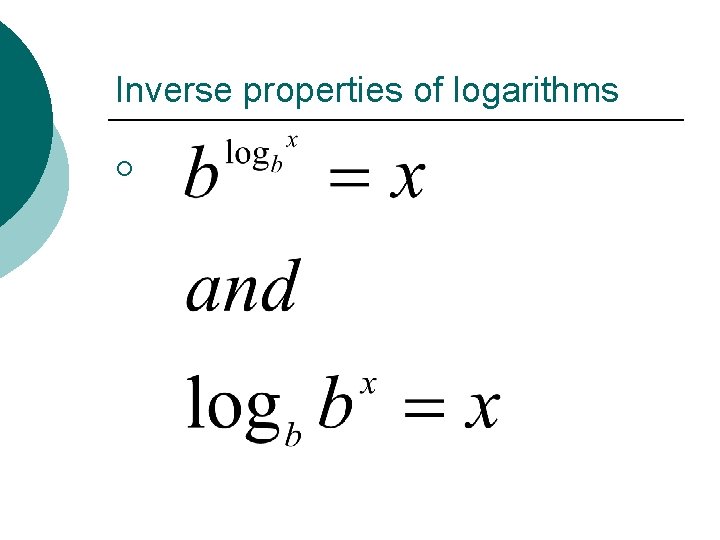
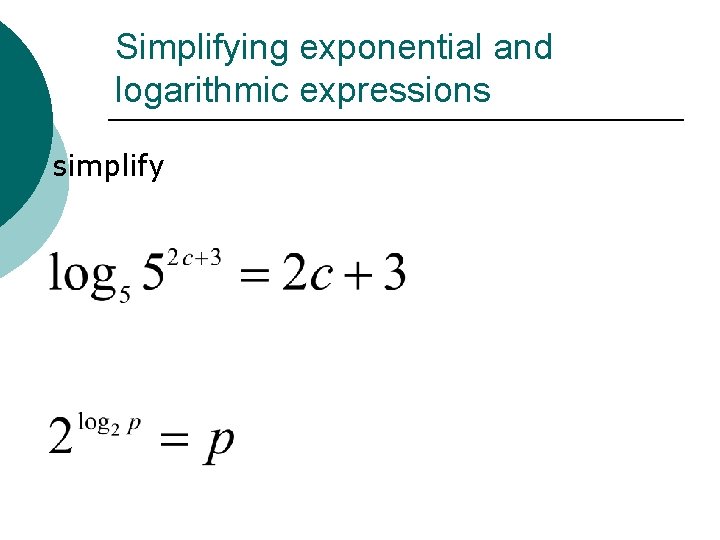
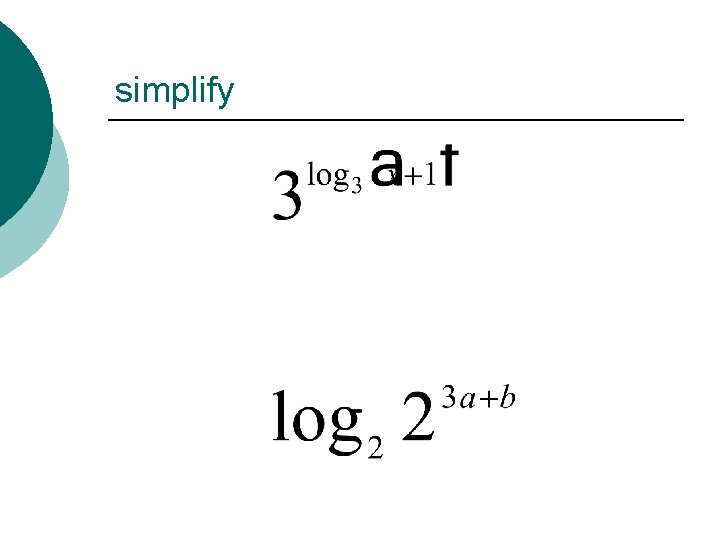











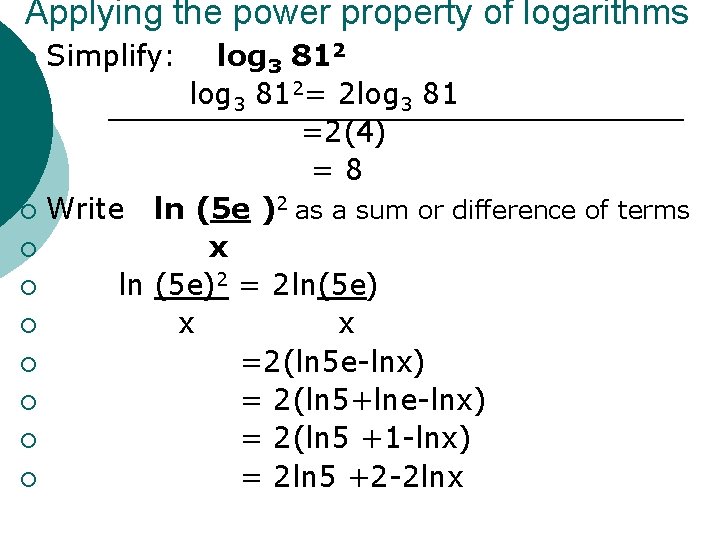

- Slides: 20

Lesson 72 Using the properties of logarithms

Log is exponent ¡ ¡ Since a logarithm is the exponent applied to a base to obtain a given value, bx = a is equivalent to logba=x

Inverse of exponential function The definition of a logarithm can be used to find the inverse of an exponential function. ¡ y= bx ¡ Inverse x= by ¡ Log form of inverse logbx=y ¡

Graphs of inverse functions are reflective images of each other ¡ with respect to the ¡ line y=x ¡ The parent function(red) ¡ y = bx for b>1 ¡ And the inverse y=logbx ¡ (green) ¡
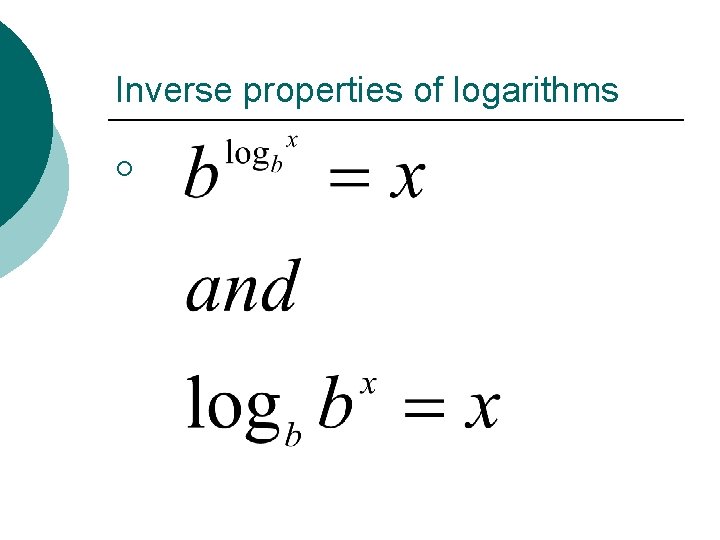
Inverse properties of logarithms ¡
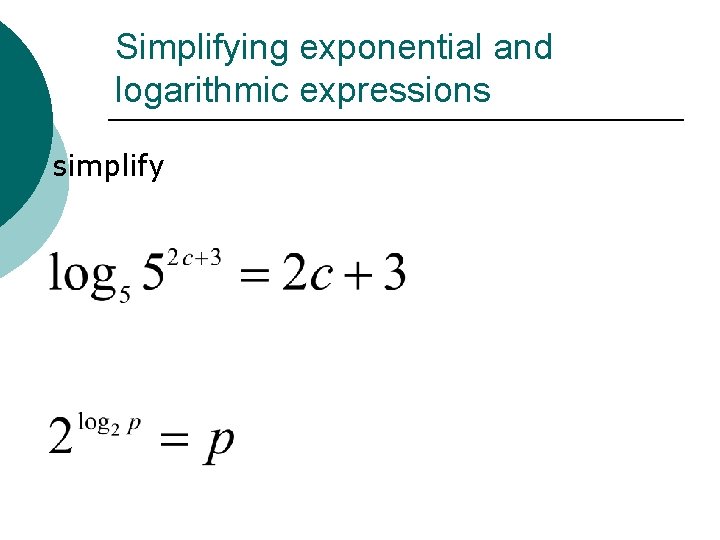
Simplifying exponential and logarithmic expressions ¡ simplify
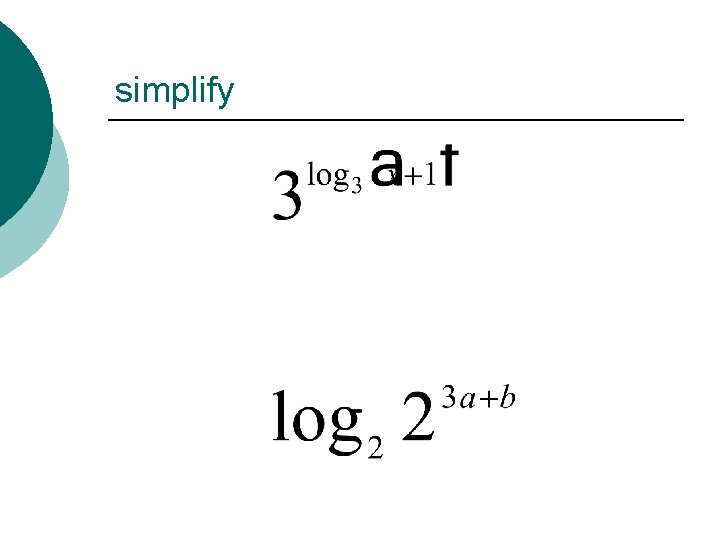
simplify

Change of base formula Most calculators calculate logarithms in base 10 or base e only. One way a logarithm with a base other than 10 or e can be evaluated is by applying the change of base formula. ¡ for a>0 and a not equal to 1 and any base b such that b>0 and b is not equal to 1 ¡ ¡ ¡ logb x = logax logab

Evaluating a log by changing the base Evaluate: log 4 8 ¡ log 4 8= log 8 ¡ log 4 ¡ Or change to base 2 because 4 and 8 are powers of 2 ¡ log 48 = log 28 = 3 ¡ log 24 2 ¡

evaluate ¡log 8127 ¡log 3264

Product property of logarithms ¡ ¡ For any positive numbers, m, n and b( b is not equal to 1) logbmn = logbm+logbn

Approximating the logarithm of a product Find the approximate value of ¡ Log 363 ( use log 37 =1. 7712) ¡ log 363= log 3(7 x 32) ¡ =log 37+log 332 ¡ = log 37+ 2 ¡ =1. 7712 + 2 = 3. 7712 ¡ Check by 33. 7712=? ¡

approximate ¡ log 60 ( use log 6=. 7782) ¡ log 280 (use log 25 = 2. 322) ¡ log 2400 (use log 24= 1. 3802)

Quotient property of logarithms ¡ For any positive numbers m, n, and b ( b is not equal to 1) ¡ logb m ¡ n ¡ ¡= logbm - logbn

Approximating the logarithm of a quotient ¡ ¡ ¡ Approximate log 46 = log 4 48 8 = log 448 -log 48 = 2. 7925 -1. 5 =1. 2925 (use log 448=2. 7925 and log 48=1. 5)

Natural log ¡ Approximate the value of ¡ (use ln 3=1. 0986) ¡ ln e 4 = ¡ ln e 4 - ln 3 3 ¡ = 4 - 1. 0986 ¡ = 2. 9014 ln e 4 3

approximate ¡ log 3 25 (use log 3125=4. 3949 and log 3 5= 1. 4650 ¡ ¡ ln e 6 4 (use ln 4 = 1. 3863)

Power property of logarithms ¡ For any real number p and positive numbers a and b (b is not equal to 1) ¡Logb p a = p logba
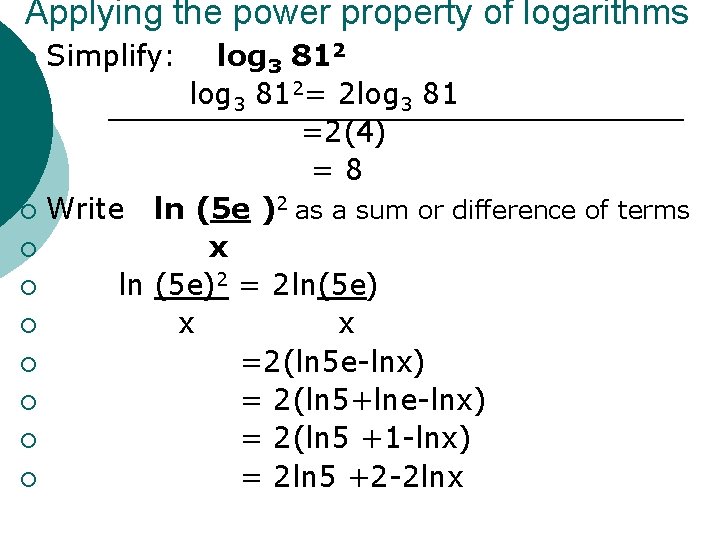
Applying the power property of logarithms log 3 812 ¡ log 3 812= 2 log 3 81 ¡ =2(4) ¡ =8 ¡ Write ln (5 e )2 as a sum or difference of terms ¡ x ¡ ln (5 e)2 = 2 ln(5 e) ¡ x x ¡ =2(ln 5 e-lnx) ¡ = 2(ln 5+lne-lnx) ¡ = 2(ln 5 +1 -lnx) ¡ = 2 ln 5 +2 -2 lnx ¡ Simplify:

simplify ¡ log 4 643 Write as a sum or difference of terms ¡ ln ( 4 e)x ¡ y ¡