Lesson 7 Iterations Loops In daily life we

Lesson 7 Iterations (Loops) Ø In daily life, we often do something repeatedly. Eg, we brush our teeth everyday. We construct a building floor by floor in the same way. Ø Moreover, we do something repeatedly as long as a certain condition is satisfied. Eg, we breathe while we are alive. We construct a building floor by floor while the roof is not yet reached. Ø In computation, we frequently execute a set of statements repeatedly while a condition (while-condition) is satisfied. 1

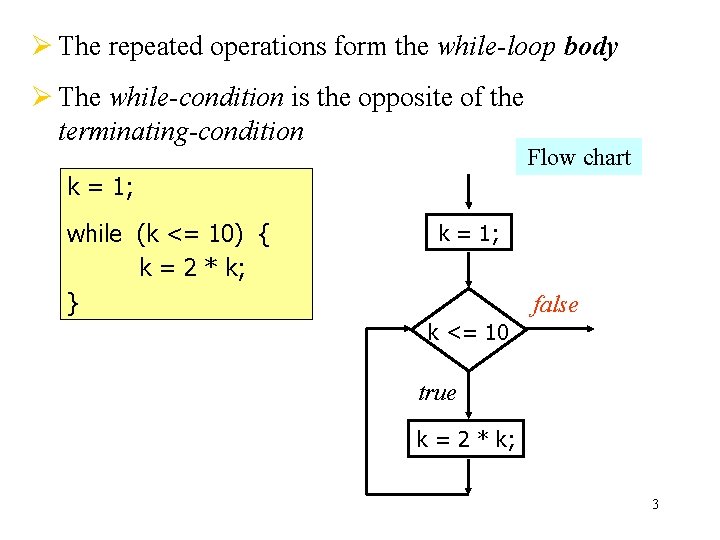
Ø To find the smallest integer that is a power of two, 2 k, and it is larger than 10 Idea: Compute 21, 22, 23, … one by one while the result is less than or equal to 10 k = 1; terminating condition if (k > 10) <stop> k = 2 * k; A while-loop version if (k > 10) <stop> k = 2 * k; while (k <= 10) { k = 2 * k; } if (k > 10) <stop> k = 2 * k; . . . k = 1; opposite while condition repeated operation 2

Ø The repeated operations form the while-loop body Ø The while-condition is the opposite of the terminating-condition Flow chart k = 1; while (k <= 10) { k = 2 * k; } k = 1; false k <= 10 true k = 2 * k; 3

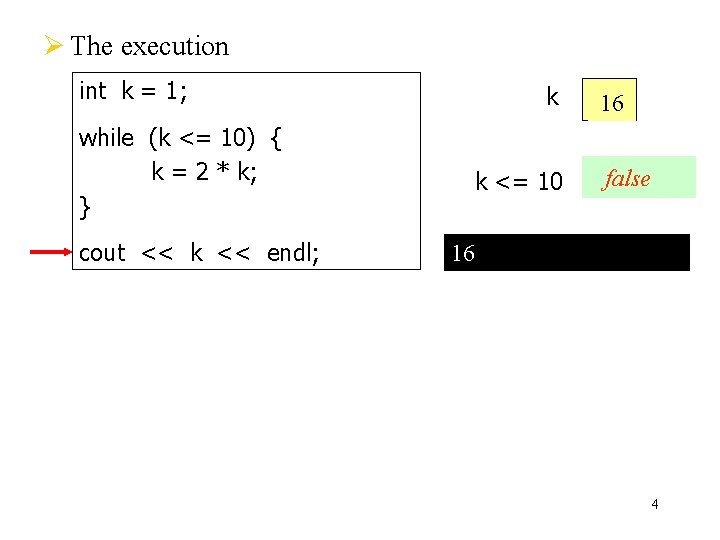
Ø The execution int k = 1; while (k <= 10) { k = 2 * k; } cout << k << endl; k k <= 10 2481 16 false true 16 4

int k = 1; while (k <= 10) { k = 2 * k; } Iteration k k 10 Before 1 true After the 1 st round 2 true After the 2 nd round 4 true After the 3 rd round 8 true After the 4 th round 16 false Trace table 5

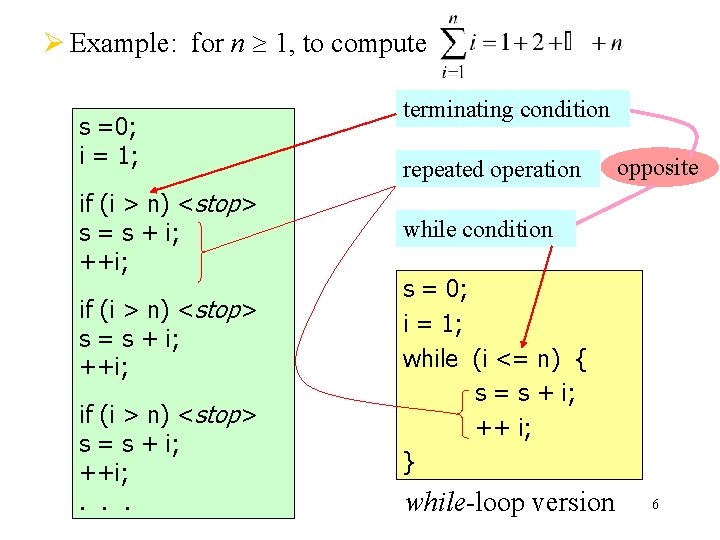
Ø Example: for n 1, to compute s =0; i = 1; if (i > n) <stop> s = s + i; ++i; . . . terminating condition repeated operation opposite while condition s = 0; i = 1; while (i <= n) { s = s + i; ++ i; } while-loop version 6

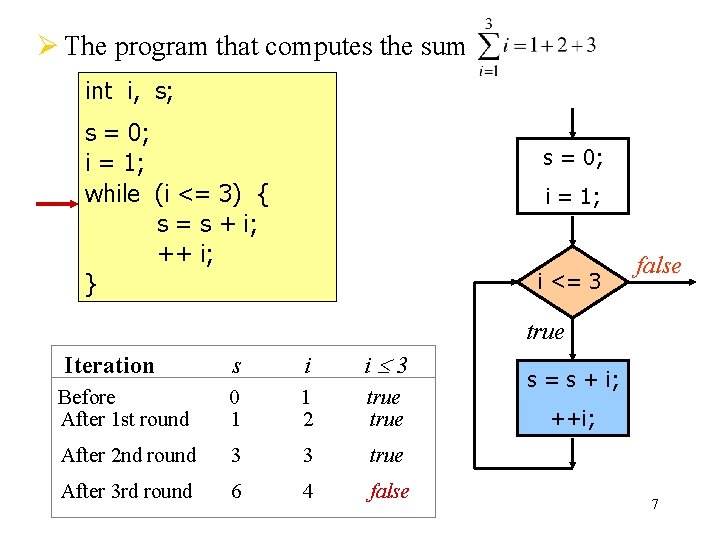
Ø The program that computes the sum int i, s; s = 0; i = 1; while (i <= 3) { s = s + i; ++ i; } s = 0; i = 1; i <= 3 false true Iteration s i i 3 Before After 1 st round 0 1 1 2 true After 2 nd round 3 3 true After 3 rd round 6 4 false s = s + i; ++i; 7

Ø The body of a while loop can be a single statement, or a compound statement. int k = 1; while (k <= 10) k = 2 * k; Eg 1 int i, s; Eg 2 s = 0; i = 1; while (i <= 3) { s = s + i; ++ i; } What is wrong? int k = 1; while (k <= 10); k = 2 * k; 8

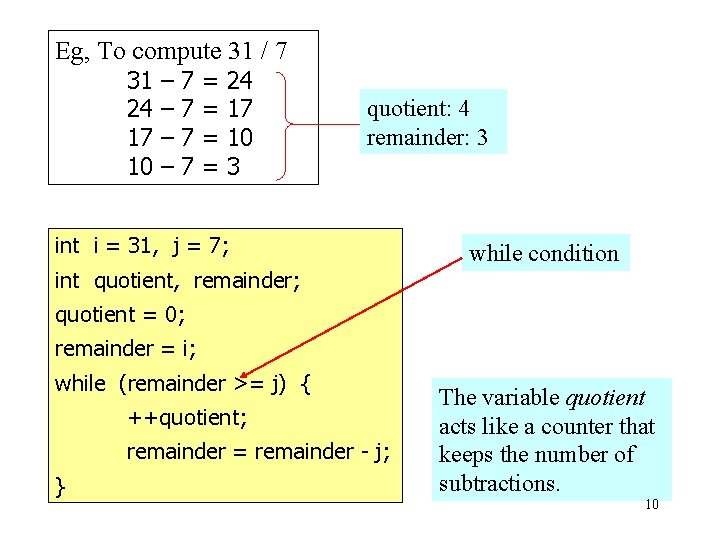
Ø To compute the integer division, i / j , using a Pascal adder (NO division), assuming that i and j are positive Idea: repeatedly subtract j from i while the remainder is equal to or larger than i. The quotient is equal to the number of subtractions. Eg, To compute 31 / 7 31 24 17 10 – – 7 7 = = 24 17 10 3 quotient: 4 remainder: 3 9

Eg, To compute 31 / 7 31 24 17 10 – – 7 7 = = 24 17 10 3 quotient: 4 remainder: 3 int i = 31, j = 7; int quotient, remainder; while condition quotient = 0; remainder = i; while (remainder >= j) { ++quotient; remainder = remainder - j; } The variable quotient acts like a counter that keeps the number of subtractions. 10

int i = 31, j = 7, quotient, remainder; quotient = 0; remainder = i; while (remainder >= j) { ++quotient; remainder = remainder - j; } quotient 0 remainder 31 remainder j true 1 1 24 true 2 2 17 true 3 3 10 true 4 4 3 false Iteration 0 is the moment when the condition is checked for the first time. Iteration 1 is the moment when the cond. is checked for the 2 nd time, etc. 11

What is the output of the following program? int x = 2, n = 5, p = 1; 32 while ( n != 0) { if (n%2 == 1) p = p * x; n = n / 2; x = x * x; } cout << p; p n x n != 0 1 2 2 32 5 2 1 0 2 4 16 256 true false 12

Ø A function that computes xn double power( double x, int n) { double p = 1. ; while ( n != 0) { if (n%2 == 1) p = p * x; n = n / 2; x = x * x; } return p; } int main() { double x = 2. ; cout. precision( 16 ); for (int i=0; i<=50; i=i+10) cout << x << "^" << i << " = " << power(x, i) << endl; } 2^0 = 1 2^10 = 1024 2^20 = 1048576 2^30 = 1073741824 2^40 = 1099511627776 13 2^50 = 1125899906842624

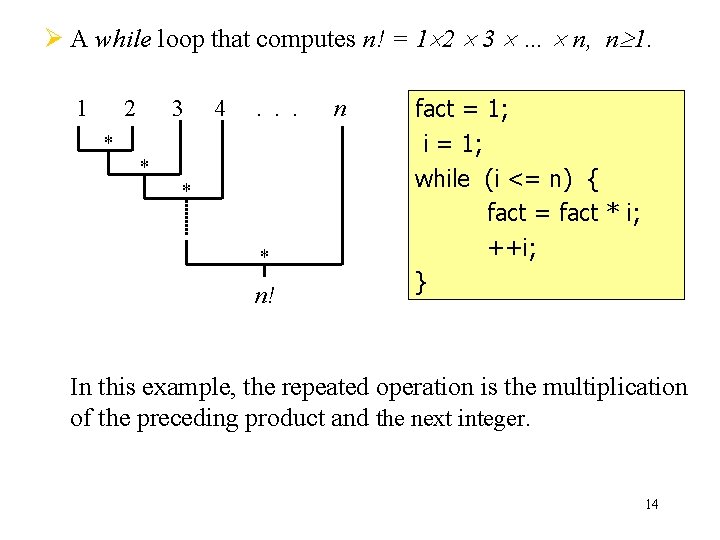
Ø A while loop that computes n! = 1 2 3 … n, n 1. 1 2 3 4 . . . * * n! n fact = 1; i = 1; while (i <= n) { fact = fact * i; ++i; } In this example, the repeated operation is the multiplication of the preceding product and the next integer. 14

n = 4; fact = 1; i = 1; while (i <= n) { fact = fact * i; ++i; } fact 1 i n true 1 1 2 true 2 2 3 true 3 6 4 true 4 24 5 false Iteration No. 0 15

Ø The last example belongs to a major kind of while loops that have the structure <init-stat> while (<bool-expr>) { <repeated-stat> <update-stat> } fact = 1; //while-loop version i = 1; while (i <= n) { fact = fact * i; ++i; } Ø A for statement is equivalent to such while loop structure for (<init-stat>; <bool-expr>; <update-stat>) <repeated-stat> fact = 1; for ( i=1; i<=n; ++i) fact = fact * i; //for-loop version 16

Ø A function that computes n! int fact( int n) { int i, fact = 1; for (i=1; i<=n; ++i) fact = i * fact; return fact; } int main() { for (int i=0; i<=5; ++i) cout << i << "! = " << fact(i) << endl; } 0! = 1 1! = 1 2! = 2 3! = 6 4! = 24 5! = 120 17

Ø To compute 1 + 2 + 3 +. . . + n. s = 0; i = 1; while (i <= n) { s = s + i; ++ i; } s = 0; for ( i=1; i<=n; ++i) s = s + i; for-loop version while-loop version 18

Ø To compute , for n 0. Ø A naïve way s = 1. 0; for ( i=1; i<=n; ++i) { s = s + pow( x, i); } Ø What is the problem? 19

Ø A better way to compute , for n 0. Make use of the relation that every term is equal to the previous term times x. term = 1. 0; s = 1. 0; for ( i=1; i<=n; ++i) { term = term * x ; s = s + term; } 20

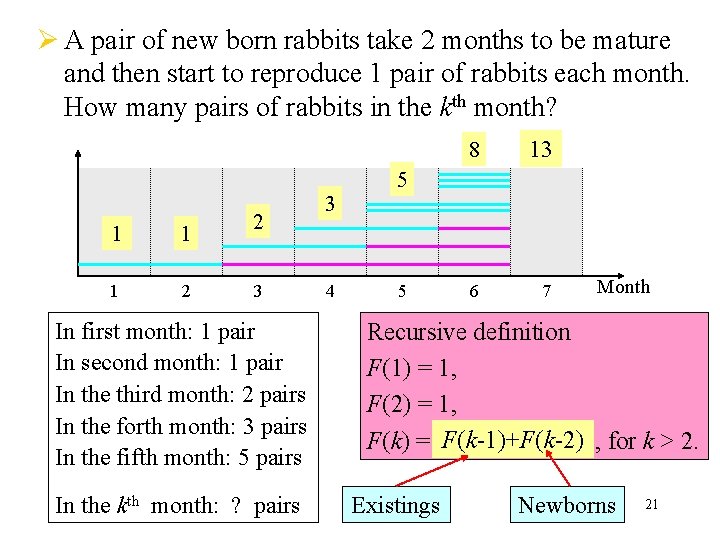
Ø A pair of new born rabbits take 2 months to be mature and then start to reproduce 1 pair of rabbits each month. How many pairs of rabbits in the kth month? 1 1 1 2 2 3 In first month: 1 pair In second month: 1 pair In the third month: 2 pairs In the forth month: 3 pairs In the fifth month: 5 pairs In the kth month: ? pairs 3 4 8 13 6 7 5 5 Month Recursive definition F(1) = 1, F(2) = 1, F(k) = F(k-1)+F(k-2) ? ? ? , for k > 2. Existings Newborns 21

Scream 22

Ø The sequence: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, . . . in which each number is the sum of the two preceding numbers, appears in many different areas of mathematics and is useful in analysis. Ø This sequence is called Fibonacci sequence Leonardo Pisano (Fibonacci) 23

Ø To write a program that computes the kth Fibonacci Number 1 2 3 4 5 6 7 8 - 1 1 2 3 5 8 13 21. . . oldf f newf oldf … 0 th iteration f newf oldf 1 st iteration 2 nd iteration newf f newf 3 rd iteration Ø Keep 3 variables, initialized as in the 0 th iteration. Move k-1 steps forward. f will then equal the kth Fibonacci No. Ø In each iteration, oldf = f; ? f = ? newf; newf = ? oldf + f; 24

int k = 4, oldf, f = 1, newf = 1; i = 2; while (i <= k) { oldf = f; f = newf; newf = oldf + f; ++i; } Oldf f newf i i k - 1 1 2 true 1 1 2 3 true 1 2 3 4 true 2 3 5 5 false 25

Ø The while loop for computing the Fibonacci number can be re-written using a for loop. The while loop version i = 2; while (i <= k) { oldf = f; f = newf; newf = oldf + f; ++i; } The for loop version for (i = 2; i <= k; ++i) { oldf = f; f = newf; newf = oldf + f; } 26

Ø Two common errors in coding iterations ØInfinite loop (Run-time error) If the update statement, eg, ++i; , is mistakenly omitted, the while-condition will always be true and the loop will continue forever. ØVoid loop (Possible logic error) If the while-condition is mistakenly put down such that it is false for the first time, the loop body will never be executed. 27

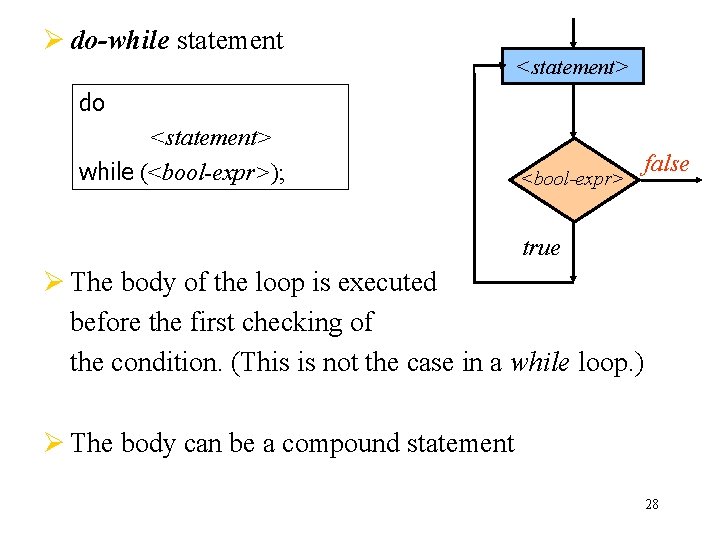
Ø do-while statement <statement> do <statement> while (<bool-expr>); <bool-expr> false true Ø The body of the loop is executed before the first checking of the condition. (This is not the case in a while loop. ) Ø The body can be a compound statement 28

What is the output value of the following code. ? int i = 0; while (i < 0) i = i + 2; cout << i; What is the output value of the following code? int j = 0; do j = j + 2; while (j < 0); cout << j; 29

Ø To compute using Taylor’s formula. Sum term by term while the absolute value of next term is greater than 0. 0000001. Ø A naïve way (What is the problem? ) term = 1. ; sum = 0. ; i = 0; do { sum = sum + term; ++i; //Assume fact(i) returns i! term = pow( x, i) / fact( i); } while (fabs( term) > 0. 0000001); 30

Ø To develop a simple and efficient program, first try to express a term in terms of the preceding term. . A recursive definition of a term, T(i) T(0) = 1, T(i) = x * T(i-1) / i. Ø Verification 31

Ø A more efficient version term = 1. ; sum = 0. ; i = 0; T(0) = 1, T(i) = x * T(i-1) / i. do { sum = sum + term; ++i; term = x * term / i; } while (fabs( term) > 0. 0000001); 32

Ø A function that computes ex double my_exp( double x) { double term = 1. , sum = 0. ; int i = 0; do { sum = sum + term; ++i; term = x * term / i; } while (sum != sum+term); return sum; } int main() { for (double x=0. ; x<=5. ; x=x+1. ) cout << "my_exp(" << x << ") = " << my_exp(x) << " (Error = " << my_exp(x) - exp( x) << ")" << endl; } my_exp(0) my_exp(1) my_exp(2) my_exp(3) my_exp(4) my_exp(5) (Error (Error = = = 1 (Error = 0) 2. 71828459046 7. 389056098930649 20. 08553692318766 54. 59815003314427 148. 4131591025765 = = = 2. 994566400404963 e-016) -1. 597246640505645 e-015) -6. 923281392623437 e-015) 2. 554206846028251 e-014) -6. 034062138837726 e-014) 33

Guidelines on loops ØUse for-loop if Øthe computation can be indexed by a variable, and Øthe number of iterations is known ahead ØEg, for n 1, to computes n! = 1 2 3 … n for n 1, to compute 1 + 3 + 5 +. . . + (2 n+1). for n 0, to compute 34

Guidelines on loops ØUse while-loop if Øthe for-loop is not applicable, and Øthe while-cond. must be checked before executing the body ØUse do-while loop if Ø the for-loop is not applicable, and Øthe body must be executed at least once ØEg, To compute 21, 22, 23, … one after one until the result is larger than n To compute ex by summing the terms in the Taylor’s formula while the absolute value of next term is greater than 0. 0000001. 35

Break statement Ø is used to jump out of a loop or a switch block (1 level) Ø may impair the clarity of a program if mis-used. int i, j, k; 3 for (i=0; i<10; ++i) { j = i + 1; k = i + 2; if (i*i + j*j == k*k) break ; } cout << i; 36

bool leave = false; int n = 0; do { ++n; cout << "leave is " << leave << endl; if (leave) break; else leave = true; } while (n != 0); cout << "n is " << n << endl; leave is 0 leave is 1 n is 2 37

int i = 0; do { cout << "i = " << i << endl; switch (i) { case 1: i = i + 2; break; default: ++i; } if (i > 4) break; } while (true); cout << "You are safe now!n"; cout << "Finally, i = " << i << endl; i = 0 i = 1 i = 3 i = 4 You are safe now! Finally, i = 5 38

What is the output of the following program? int s = 0; for (int i=1; i<=10; ++i) { s = s + i; if (s >= 6) break; s = s + 1; } cout << s; i s s >= 6 1 1 4 8 false true 2 3 39

Reading Assignment Ø Chapters 7 of the Text, p. 414 -458 40