Lesson 7 7 Numerical Approximations of Integrals What

Lesson 7 -7 Numerical Approximations of Integrals -- What we do when we can’t integrate a function Riemann Sums Trapezoidal Rule

Strategies for Integrals that we can’t do • Use Riemann Sums – left-hand or right-hand, to approximate the area under the curve (i. e. , the value of the definite integral) • Use the Trapezoidal Rule to approximate the area under the curve – The trapezoidal rule gives us an average of the right and left hand Riemann Sum approximations – The graph of f The trapezoidal rule will: concave down underestimate the area concave up overestimate the area.

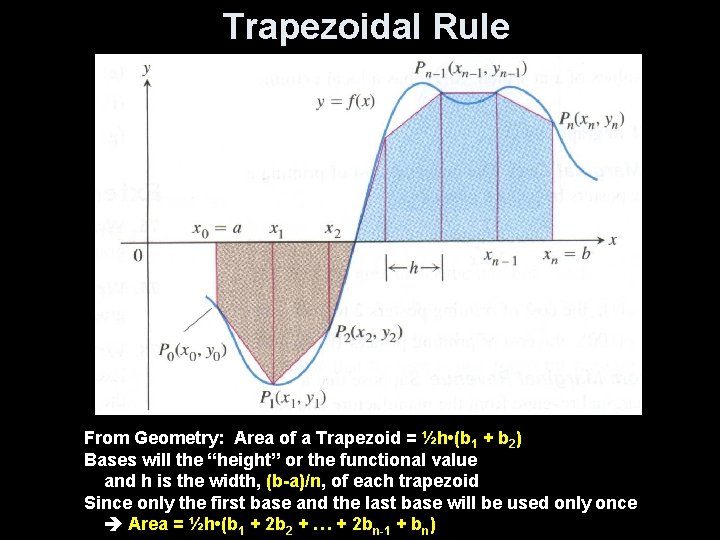
Trapezoidal Rule From Geometry: Area of a Trapezoid = ½h • (b 1 + b 2) Bases will the “height” or the functional value and h is the width, (b-a)/n, of each trapezoid Since only the first base and the last base will be used only once Area = ½h • (b 1 + 2 b 2 + … + 2 bn-1 + bn)

Example 1 x=π Use the trapezoidal rule with n = 4 to approximate h = (b-a)/n = (π-0)/4 = π/4 n 0 1 2 3 4 f(x) sin(0) =0 sin(π/4) = 0. 7071 sin(π/2) = 1 sin(3π/4) = 0. 7071 sin(π) = 0 ∫ sin x dx x=0 Area = ½ h (b 1 + b 2) Area 1 = ½ h (b 1 + b 2) = π/8(0 + 0. 7071) Area 2 = ½ h (b 1 + b 2) = π/8(0. 7071 + 1) Area 3 = ½ h (b 1 + b 2) = π/8(1 + 0. 7071) Area 4 = ½ h (b 1 + b 2) = π/8(0. 7071 + 0) Area. T = Ai = (π/8)[2(0. 7071) + 2(1. 7071)] = 1. 89612 x=π 1 2 3 4 ∫ sin x dx = 2 x=0

Example 2 x=1 Use the trapezoidal rule with n = 5 to approximate h = (b-a)/n = (1 -0)/5 = 1/5 n 0 1 2 3 4 5 f(x) f(0) = 1 f(1/5) = 1. 2214 f(2/5) = 1. 4918 f(3/5) = 1. 8221 f(4/5) = 2. 2255 f(1) = 2. 7183 ∫e x² dx x=0 Area = ½ h (b 1 + b 2) Area 1 = ½ h (b 1 + b 2) = 1/10(1 + 1. 2214) Area 2 = ½ h (b 1 + b 2) = 1/101. 2214 + 1. 4918) Area 3 = ½ h (b 1 + b 2) = 1/10(1. 4918 + 1. 8221) Area 4 = ½ h (b 1 + b 2) = 1/10(1. 8221 + 2. 2255) Area 5 = ½ h (b 1 + b 2) = 1/10(2. 2255 + 2. 7183) Area. T = Ai = (1/10)[1 + 2(1. 2214) + 2(1. 4918) + 2(1. 8221) + 2(2. 2255) + 2. 7183] = 1. 72399 x=1 123 4 5 ∫e x² dx = 1. 46265 x=0 note: calculator did a numeric apx

Pond Example 50 30 45 h = 20 =(b-a)/n n=7 40 45 40 Area = ½ h (b 1 + b 2) Area 1 = ½ h (b 1 + b 2) = 10(0 + 40) Area 2 = ½ h (b 1 + b 2) = 10(40 + 50) Area 3 = ½ h (b 1 + b 2) = 10(50 + 45) Area 4 = ½ h (b 1 + b 2) = 10(45 + 30) Area 5 = ½ h (b 1 + b 2) = 10(30 + 45) Area 6 = ½ h (b 1 + b 2) = 10(45 + 40) Area 7 = ½ h (b 1 + b 2) = 10(40 + 0) Area. T = Ai = 400 = 950 = 750 = 850 = 400 = 5000

Approximating the Error of the Estimate If f has a continuous second derivative on [a, b], then x=b the error E in approximating ∫ f(x) dx by the x=a trapezoidal rule is: (b-a)³ E ≤ ---- max |f ’’(x)| 12 n² (b – a)³ n² ≤ ----- max |f ’’(x)| 12 E where a ≤ x ≤ b (always round up to next whole # when calculating n)

Example 3 Use the error formula to find the maximum possible error in approximating the integral, with n = 4. 1 ∫ ----- dx x=0 x + 1 x=1 f(x) = (x + 1)-1 f’(x) = -(x+1)-2 f’’(x) = 2/(x+1)-3 (b-a)³ E ≤ ---- max |f ’’(x)| 12 n² (1 -0)³ E ≤ ---- |2| 12 • 4² E ≤ 0. 01042 where a ≤ x ≤ b (at x = 0 )

Example 4 Use the error formula to find n so that the error in the approximation of the definite integral is less than 0. 00001. 1 ∫ ----- dx x=0 x + 1 x=1 f(x) = (x + 1)-1 f’(x) = -(x+1)-2 f’’(x) = 2/(x+1)-3 (b – a)³ n² ≥ ----- max |f ’’(x)| 12 E (1 – 0)³ [2] n² ≥ ---------12 (0. 00001) n² ≥ 16666. 67 n ≥ 129. 1 n = 130 (always round up to next whole # when calculating n)

Summary & Homework • Summary: – Riemann Sums can be used to get approximations to definite integrals that we don’t know how to integrate – The error used to approximate the integral can be calculated – The number of sub-intervals required to keep the error bounded can be calculated • Homework: – pg 527 – 529: 7, 8, 9