Lesson 7 4 Solving by Multiplication There are

Lesson 7. 4 Solving by Multiplication � � � � There are two different methods for multiplying to eliminate a variable: Method #1: You multiply one of the equations by a certain number to get it to match the coefficients in the 2 nd equation. Ex. 1: x + y = 3 → 2 x + 2 y = 6 (notice each number is multiplied by 2) 2 x – 3 y = 16 → 2 x – 3 y = 16 (you can eliminate the x-variable) You can multiply each term in the 1 st equation by 2 to get the coefficients of x to match up. From here you can use the steps in 7. 3 to solve the problem. Method #2: Sometimes you have to multiply each equation by different numbers to get the coefficients to match-up. Ex. 2: 2 x – 3 y = 2 → 10 x – 15 y = 10 (each term is multiplied by 5) 5 x + 4 y = 28 → 10 x + 8 y = 56 (each term is multiplied to 2) It does not matter which variable you eliminate. Lets pick x, so we look at the coefficients of x and find the lcm (least common multiple/the smallest number that 2 and 5 both go into). Since 10 is the smallest number that 2 and 5 go into, we multiply the top equation by 5 and the bottom equation by 2). We can now use the steps from 7. 3 to solve this problem.

Use elimination to solve the system of equations. Multiply the first equation by – 2 so the coefficients of the y terms are additive inverses. Then add the equations. Multiply by – 2. Add the equations. Divide each side by – 1. Simplify.

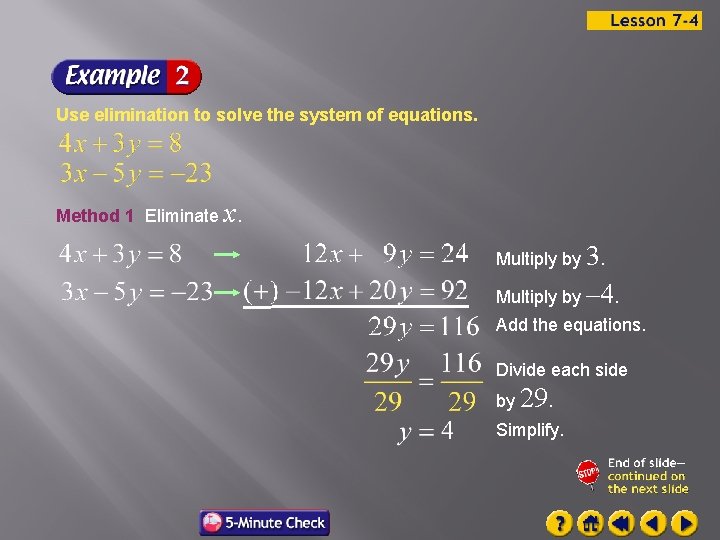
Use elimination to solve the system of equations. Method 1 Eliminate x. Multiply by 3. Multiply by – 4. Add the equations. Divide each side by 29. Simplify.

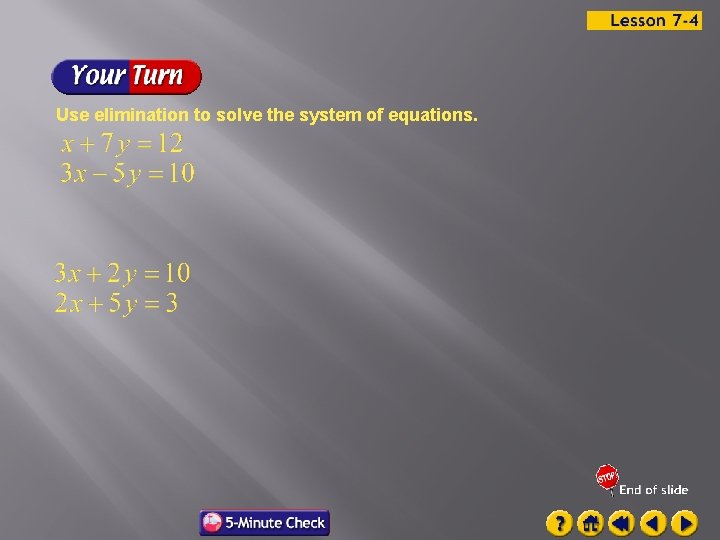
Use elimination to solve the system of equations.