Lesson 7 4 Partial Fractions Fractional Integral Types

Lesson 7 -4 Partial Fractions

Fractional Integral Types • Type I – Improper: – Degree of numerator ≥ degree of denominator – Start with long division • Type II – Proper: – Degree of numerator < degree of denominator – Check common forms or decompose into partial fractions – Repeated terms require special techniques • Type III – Variations of Arctan: – U-substitution used a lot • Type IV – Variations of Arcsin: – U-substitution used a lot

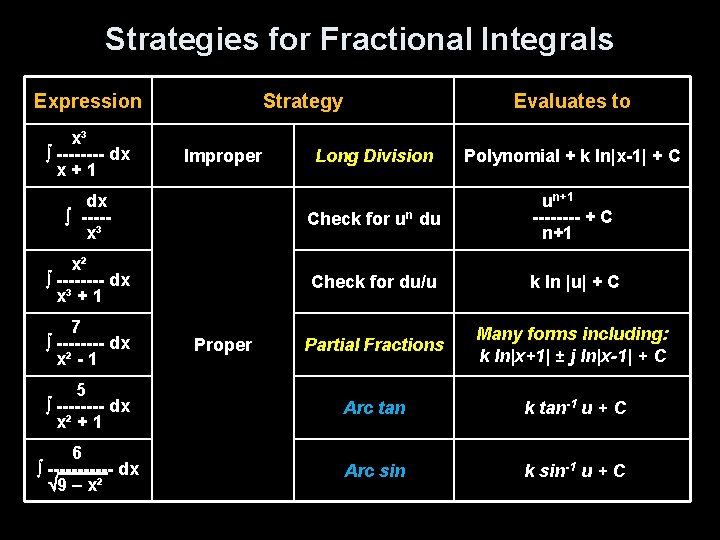
Strategies for Fractional Integrals Expression x³ ---- dx x+1 Strategy Long Division Polynomial + k ln|x-1| + C dx ----x³ Check for un du un+1 ---- + C n+1 x² ---- dx x³ + 1 Check for du/u k ln |u| + C Partial Fractions Many forms including: k ln|x+1| ± j ln|x-1| + C 5 ---- dx x² + 1 Arc tan k tan-1 u + C 6 ------ dx 9 – x² Arc sin k sin-1 u + C 7 ---- dx x² - 1 Improper Evaluates to Proper

7 -4 Example 1 x ----- dx = x-1 = = Long Division 1 dx + 1 ----- dx x-1 ln |x – 1| + C 1 x-1 x + 0 x-1 +1

7 -4 Example 2 x³ ----- dx = x+1 Long Division x² dx - x dx = = + ⅓x³ - ½x² + x - 1 dx - x² - x + 1 x+1 x³+ 0 x² + 0 x + 0 x³ + x² -x² + 0 x -x² - x x+0 x+1 -1 1 ----- dx x+1 ln |x+1| + C

Partial Fractions Example: ∫ 3 x – 1 ------- dx x² - x – 6 I) factor denominator x² - x – 6 = (x – 3) (x – 2) 3 x – 1 A B ------- = ----- + -----x² – x – 6 (x – 3) (x – 2) II) rewrite fraction III) multiply through by common denominator 3 x – 1 = A(x + 2) + B(x – 3) IV) solve one factor and substitute when x = -2 then B = 7/5 V) repeat with remaining factor(s VI) substitute A and B and integrate when x = 3 then A = 8/5 8 1 7 1 -- ---- dx + -- ----- dx 5 (x-3) 5 (x + 2) ∫ ∫ = (8/5) ln|x-3| + (7/5) ln|x+2| + C

7 -4 Example 6 Variations of Arctan: dx -------4 x² + 9 u = 2 x 1 2 x -1 ---- tan (------) + C 6 3 and a=3 dx -------(x+1)² + 4 u = x+1 k k u ----- du = --- tan-1 (---) + C u² + a² a a 1 x+1 -1 ---- tan (----) + C 2 2 and a=2 dx --------x² + 4 x + 5 x² + 4 x + 4 + 1 = (x+2)² + 1² u = x+2 and a = 1 1 x+2 -1 ---- tan (----) + C 1 1

7 -4 Example 7 Variations of Arcsin: dx ------- 9 - x² u=x 1 x -1 ---- sin (------) + C 3 3 and a=3 dx ------- 16 – (1+x)² u = x+1 k k x ----- dx = --- sin-1 (---) + C a² - x² a a 1 x+1 -1 ---- sin (----) + C 4 4 and a=4 dx -------- -4 x - x² 4 – 4 x - x² = 2² - (x+2)² u = x+2 and a = 2 1 x+2 -1 ---- sin (----) + C 2 2

Summary & Homework • Summary: – No quotient rule for integration – Compare highest power numerator vs denominator • Numerator Denominator – Use long division to simplify • Numerator < Denominator – Find common form – Use partial fractions • Homework: – pg 504 -505, Day 1: 1, 2, 3, 7 Day 2: 4, 10, 19, 40