Lesson 7 2 Substitution Keys for doing substitution

Lesson 7. 2 Substitution � � � Keys for doing substitution: Step #1: You must have a variable in one of your equations by itself. Step #2: You then take what the variable equals and substitute that value into your other equation. Step #3: You now need to solve for the variable in that equation. Step #4: Once you have found that variable, then you can find the other variable by plugging in your value of the original variable You will need to find both x and y to have a complete answer. You need to express your answer in parenthesis as (x, y)

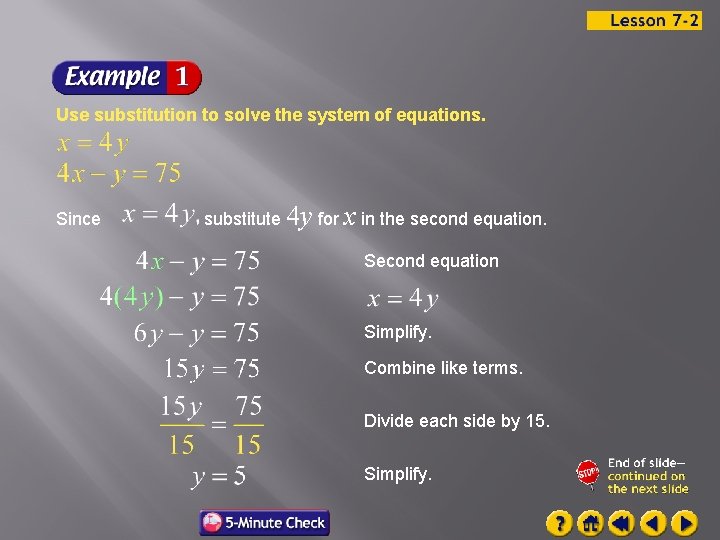
Use substitution to solve the system of equations. Since substitute 4 y for x in the second equation. Second equation Simplify. Combine like terms. Divide each side by 15. Simplify.

Use to find the value of x. First equation Simplify. Answer: The solution is (20, 5).

Use substitution to solve the system of equations. Solve the first equation for y since the coefficient of y is 1. First equation Subtract 4 x from each side. Simplify.

Find the value of x by substituting equation. for y in the second Second equation Distributive Property Combine like terms. Add 36 to each side. Simplify. Divide each side by 10. Simplify.

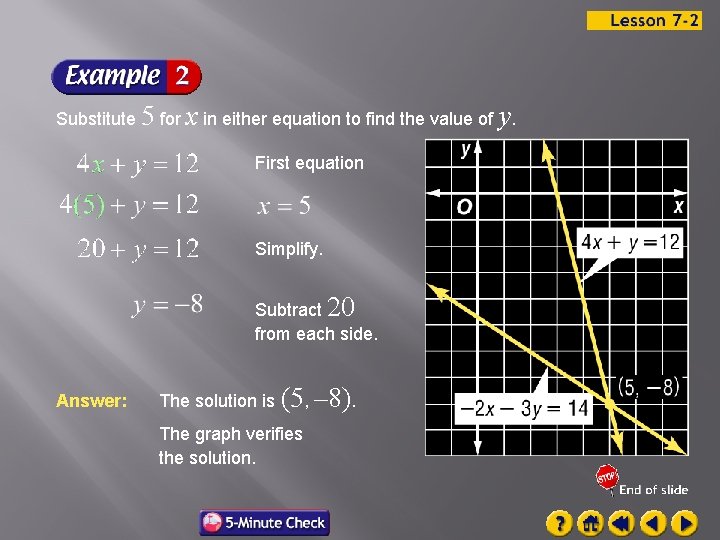
Substitute 5 for x in either equation to find the value of y. First equation Simplify. Subtract 20 from each side. Answer: The solution is (5, – 8). The graph verifies the solution.

Use substitution to solve the system of equations. Solve the second equation for y. Second equation Subtract x from each side. Simplify. Substitute for y in the first equation. First equation Distributive Property Simplify.

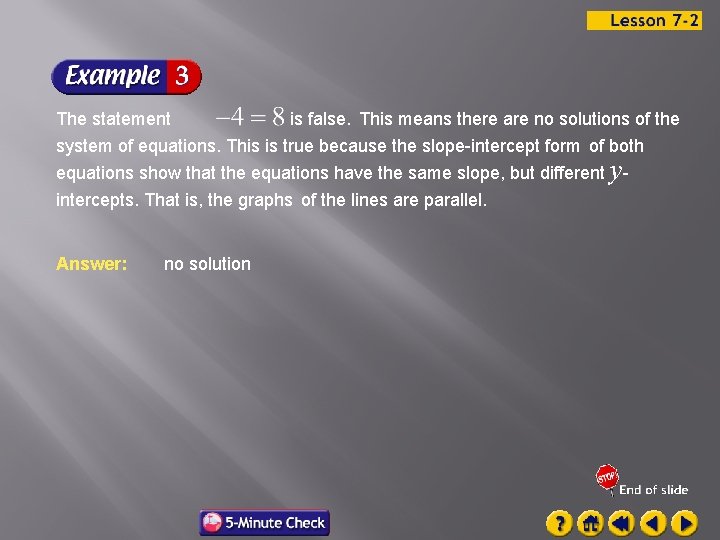
The statement is false. This means there are no solutions of the system of equations. This is true because the slope-intercept form of both equations show that the equations have the same slope, but different yintercepts. That is, the graphs of the lines are parallel. Answer: no solution

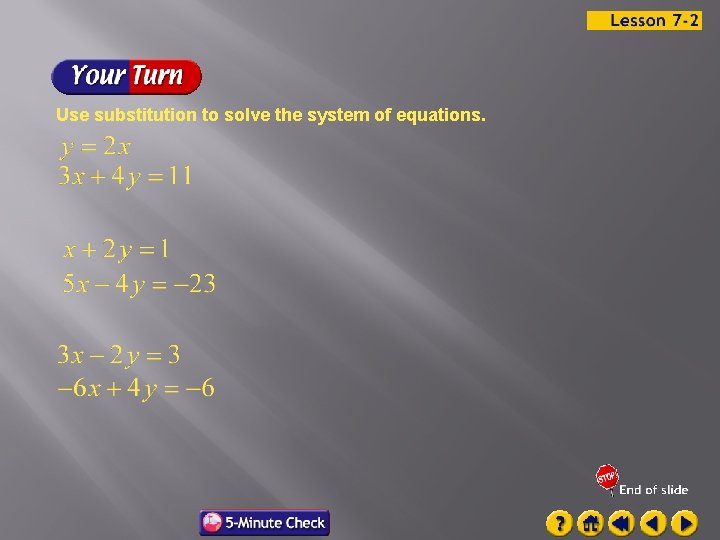
Use substitution to solve the system of equations.