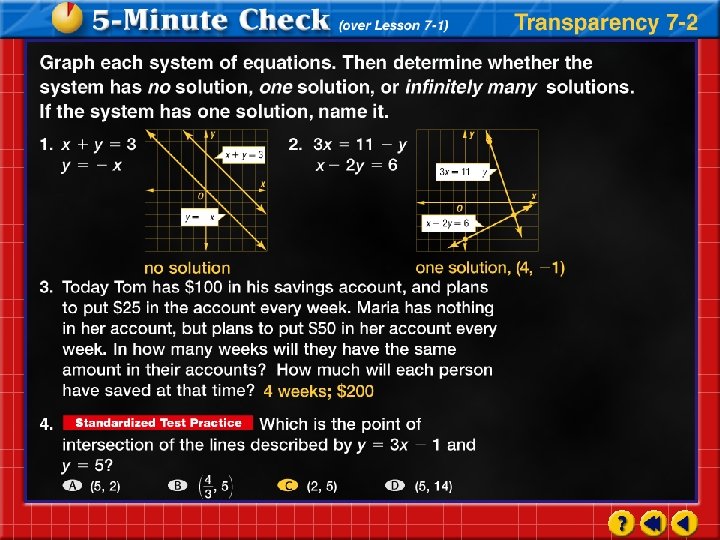
Lesson 7 2 Substitution Click the mouse button

Lesson 7 -2 Substitution

Click the mouse button or press the Space Bar to display the answers.

Objectives • Solve systems of equations by using subtraction • Solve real-world problems involving systems of equations

Vocabulary • Substitution - putting the value of one variable (in terms of the other variable) into the equation

Substitution • We have used substitution before, plugging in a constant value for x to find y in a equation of a line. y=4 x– 7 let x = 3 then y = 4(3) – 7 = 12 – 7 = 5 • Now we are using substitution to help us eliminate a variable in a system of equations (to solve them) y = 4 x – 7 and y=2 x+9 by substituting what y is (in terms of x) in the second equation for y in the first equation we get 2 x + 9 = 4 x – 7 an equation of just one variable! • We can solve this to get x = 8 and y = 25

Example 1 Use substitution to solve the system of equations. Since substitute 4 y for x in the second equation. Second equation Simplify. Combine like terms. Divide each side by 15. Use Simplify. to find the value of x. Simplify. Answer: The solution is (20, 5).

Example 2 Use substitution to solve the system of equations. Solve the first equation for y since the coefficient of y is 1. First equation Subtract 4 x from each side. Simplify.

Example 2 cont Find the value of x by substituting 12 – 2 x for y in the second equation. Second equation Distributive Property Combine like terms. Add 36 to each side. Simplify. Divide each side by 10. Simplify.

Example 2 cont Substitute 5 for x in either equation to find the value of y. First equation Simplify. Subtract 20 from each side. Answer: The solution is (5, – 8). The graph verifies the solution.

Example 3 Use substitution to solve the system of equations. Solve the second equation for y. Second equation Subtract x from each side. Substitute Simplify. for y in the first equation. First equation Distributive Property Simplify. Answer: The statement -4 = 8 is false. This means there are no solutions of the system of equations. That is, the graphs of the lines are parallel.

Example 4 Gold is alloyed with different metals to make it hard enough to be used in jewelry. The amount of gold present in a gold alloy is measured in 24 ths called karats. 24 -karat gold is or 100% gold. Similarly, 18 - or 75% gold. How many ounces of 18 - karat gold should be added to an amount of 12 -karat gold to make 4 ounces of 14 -karat gold?

Example 4 cont Let the number of ounces of 18 -karat gold and the number of ounces of 12 -karat gold. Use the table to organize the information. Total Ounces 18 -karat gold 12 -karat gold 14 -karat gold x y 4 Ounces of Gold The system of equations is and Use substitution to solve this system.

Example 4 cont First equation Subtract y from each side. Simplify. Second equation Distributive Property Combine like terms.

Example 4 cont Subtract 3 from each side. Simplify. Multiply each side by – 4. Simplify.

Example 4 cont First equation Subtract from each side. Simplify. Answer: ounces of the 18 -karat gold and of the 12 -karat gold should be used. ounces

Summary & Homework • Summary: – In a system of equations, solve one equation for a variable, and then substitute that expression into the second equation to solve • Homework: – Pg 379 12 -28 even