Lesson 7 1 Graphing Systems of Equations Definition

Lesson 7 -1 Graphing Systems of Equations

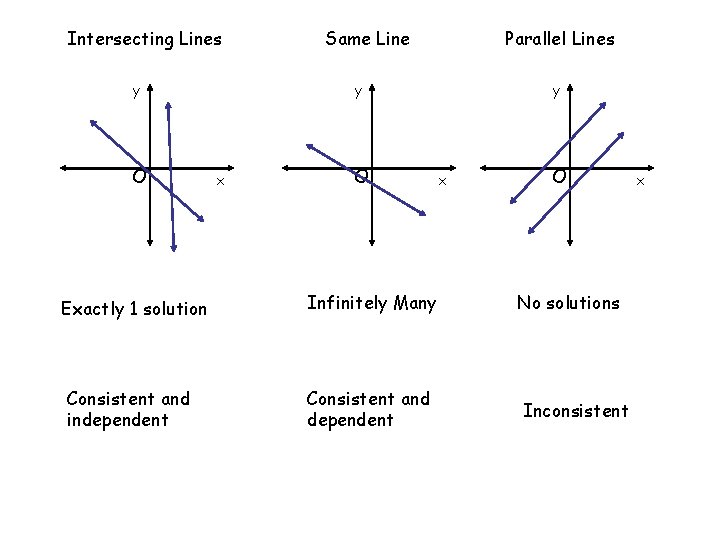
Definition • Systems of Equations- Two equations together. A solution to a system of equations has 0, 1 or an infinite number of solutions. • Consistent - If the graphs intersect or coincide, the system of equations is said to be consistent. • Inconsistent - If the graphs are parallel, the systems of equation is said to be inconsistent. • Consistent equations are independent or dependent. Equations with exactly one solution is independent. Equations with infinite solutions is dependent.

Intersecting Lines y O Exactly 1 solution Consistent and independent Same Line Parallel Lines y x O Infinitely Many Consistent and dependent y x O No solutions Inconsistent x

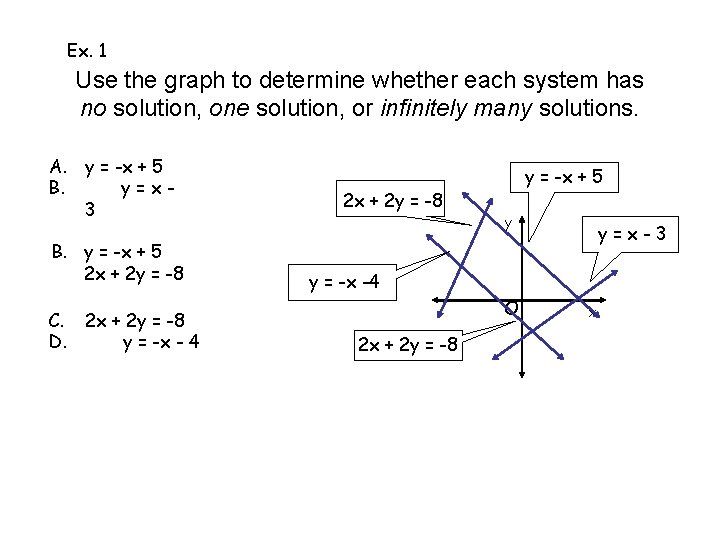
Ex. 1 Use the graph to determine whether each system has no solution, one solution, or infinitely many solutions. A. y = -x + 5 B. y=x 3 B. y = -x + 5 2 x + 2 y = -8 C. 2 x + 2 y = -8 D. y = -x - 4 2 x + 2 y = -8 y = -x + 5 y y=x-3 y = -x -4 O 2 x + 2 y = -8 x

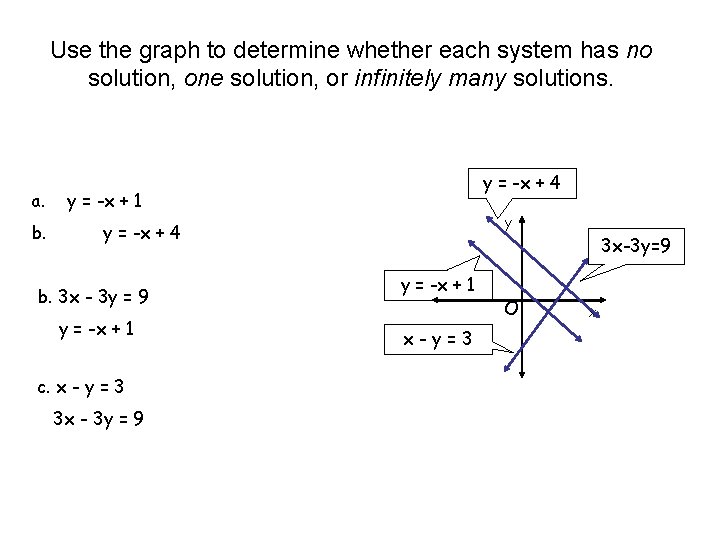
Use the graph to determine whether each system has no solution, one solution, or infinitely many solutions. a. b. y = -x + 4 y = -x + 1 y y = -x + 4 b. 3 x - 3 y = 9 y = -x + 1 c. x - y = 3 3 x - 3 y = 9 3 x-3 y=9 y = -x + 1 x-y=3 O x

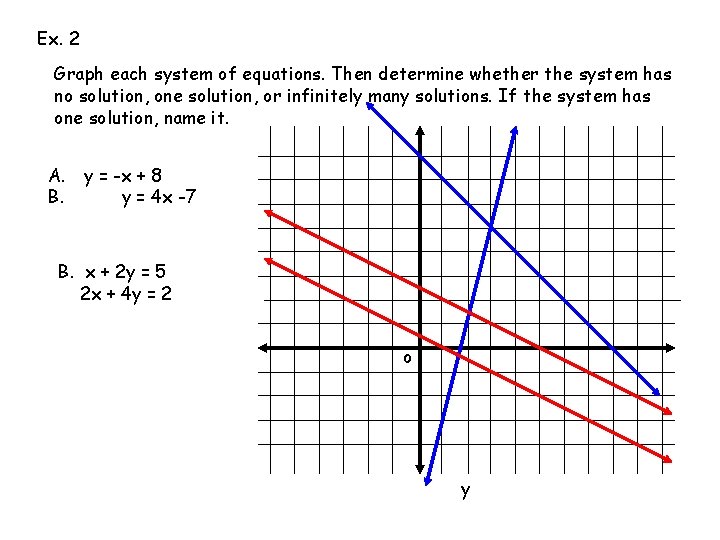
Ex. 2 Graph each system of equations. Then determine whether the system has no solution, one solution, or infinitely many solutions. If the system has one solution, name it. A. y = -x + 8 B. y = 4 x -7 B. x + 2 y = 5 2 x + 4 y = 2 o y

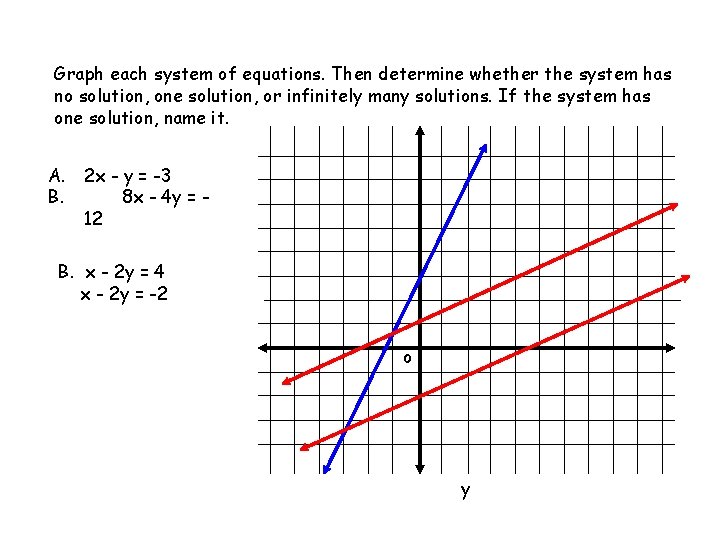
Graph each system of equations. Then determine whether the system has no solution, one solution, or infinitely many solutions. If the system has one solution, name it. A. 2 x - y = -3 B. 8 x - 4 y = 12 B. x - 2 y = 4 x - 2 y = -2 o y

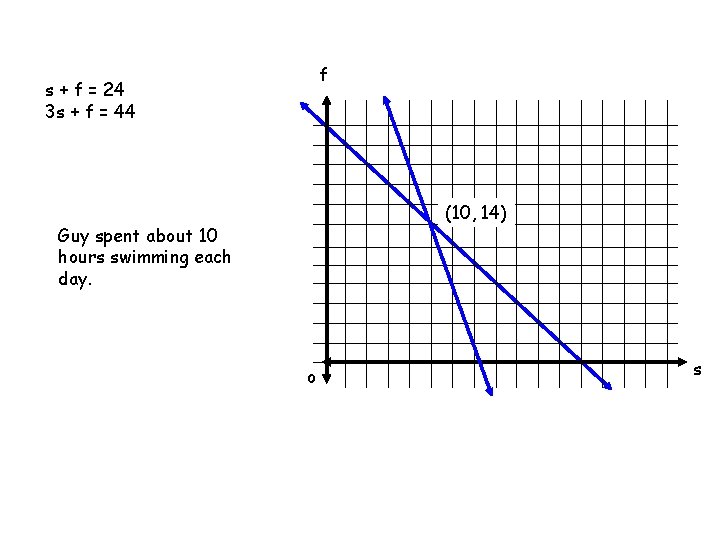
Ex. 3 Write and Solve a System of Equations If Guy Delage can swim 3 miles per hour for an extended period of time and the raft drifts about 1 mile per hour, how may hours did he swim each day if he traveled an average of 44 miles per day? Let s = the number of hours he swam and let f = the number of hours he floated each day. The number of the number of equals hours in a day hours swimming hours floating plus s The daily miles traveled 3 s + = f plus + the daily miles traveled floating 1 f 24 equals = total miles in a day 44

f s + f = 24 3 s + f = 44 (10, 14) Guy spent about 10 hours swimming each day. o s

BICYCLING: Tyler and Pearl went on a 20 -kilometer bike ride that lasted 3 hours. Because there were many steep hills on the bike ride, they had to walk for most of the trip. Their walking speed was 4 kilometers per hour. Their riding speed was 12 kilometers per hour. How much time did they spend walking? (Hint: let r = number of hours riding and w = number of hours walking. ) w r+w=3 12 r + 4 w = 20 They walked for 2 hours r