Lesson 66 Solving inequalities by adding or subtracting

Addition property of inequality • Addition property of inequality states that when the same number is added to both sides of an inequality, the statement remains true. • For any real numbers a, b, and c If a<b, then a+c<b+c If a>b, then a+c>b+c If a<b, then a+c<B+c If a>b, then a+c>b+c • •

Using the addition property of inequality • • Solve and graph the solution on a number line: x-10<-6 +10 x < 4 graph

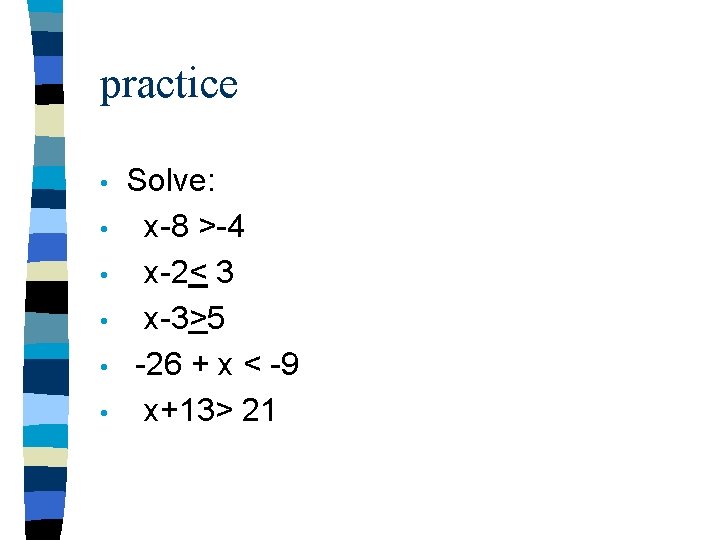
practice • • • Solve: x-8 >-4 x-2< 3 x-3>5 -26 + x < -9 x+13> 21

Subtraction property of inequality • When equal quantities are subtracted from both sides of an inequality, the inequality remains the same. • For any real numbers a, b, and c If a<b, then a-c<b-c If a>b, then a-c>b-c • •

Using subtraction • • Solve and graph the solution on a a number line. x+2 >3 -2 -2 x >1 graph

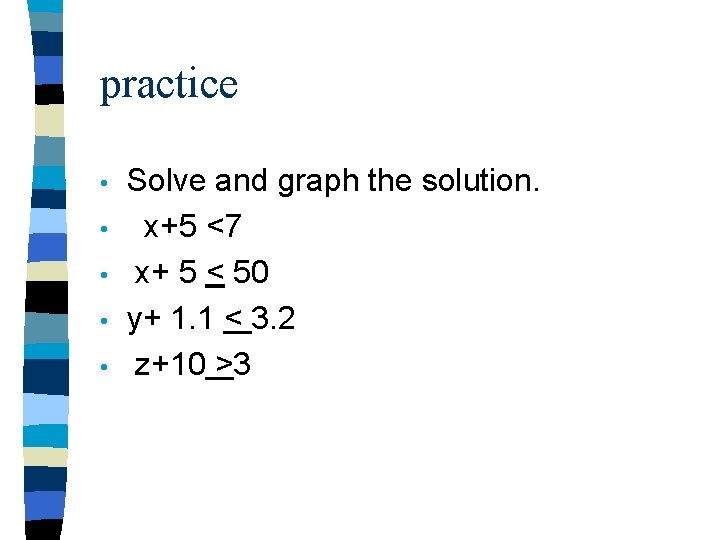
practice • • • Solve and graph the solution. x+5 <7 x+ 5 < 50 y+ 1. 1 < 3. 2 z+10 >3

Lesson 70 • Solving inequalities by multiplying or dividing

Multiplication property of inequality • • • For every real number a and b and c>0 If a>b , then ac>bc If a<b, then ab<b ac For every real number a and b, and c<0 If a>b, then ac<bc If a<b, then ac>bc

Multiplying by a positive number • • solve and graph. 1/2 x<8 2(1/2) x < 2(8) x < 16 graph

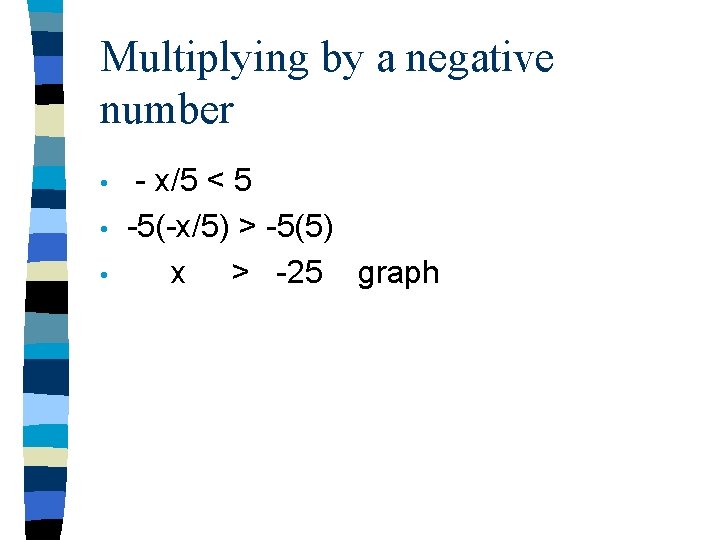
Multiplying by a negative number • • • - x/5 < 5 -5(-x/5) > -5(5) x > -25 graph

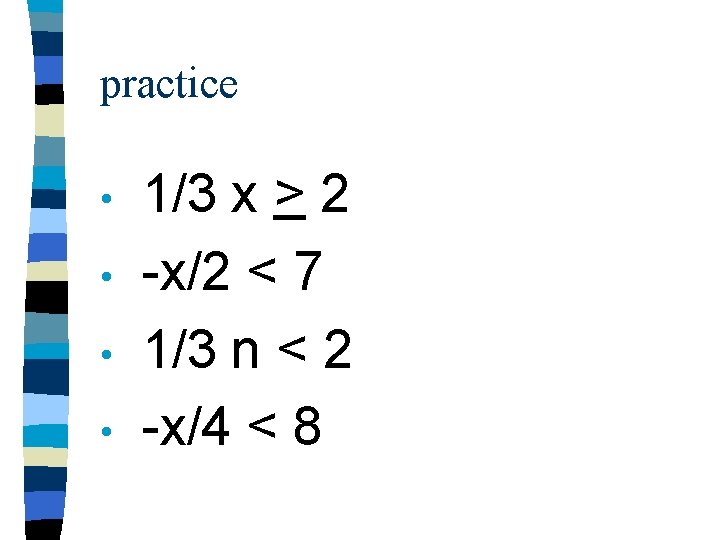
practice • • 1/3 x > 2 -x/2 < 7 1/3 n < 2 -x/4 < 8

Division property of inequality • • • For every real number a and b and c>0 if a>b, then a/c > b/c if a<b, then a/c< b/c For every real number a and b and c<0 if a>b, then a/c< b/c if a<b, then a/c > b/c

Solve and graph • • 18 > 3 r 3 3 6 > r graph r < 6 -4 m > 7 -4 m < 7 -4 -4 m < -7/4

practice • • 21 > 7 x -5 x < 30 6 w < 57 1/2 > -4 a

practice