LESSON 6 3 FINDING PERIMETER AND AREA IN

LESSON 6. 3 – FINDING PERIMETER AND AREA IN THE COORDINATE PLANE CONCEPT: DISTANCE IN THE COORDINATE PLANE EQ: HOW DO WE FIND AREA & PERIMETER IN THE COORDINATE PLANE? (G. GPE. 7) VOCABULARY: DISTANCE FORMULA, POLYGON, AREA, PERIMETER 6. 2. 2: CALCULATING PERIMETER AND AREA 1

THINK-PAIR-SHARE • Think back to the distance formula and when you used it. Take a minute and write down everything you remember about using the distance formula. • With your partner, compare your notes to see if you missed anything. • Wait to be called on and then share your answers with the class. 6. 2. 2: CALCULATING PERIMETER AND AREA 2

INTRODUCTION In the previous lesson, the distance formula was used to find the distance between two given points. In this lesson, the distance formula will be applied to perimeter and area problems. A polygon is a two-dimensional figure formed by three or more segments. We will use the distance formula to find the perimeter, or the sum of the lengths of all the sides of a polygon, and the area, the number of square units inside of a polygon, such as finding the amount of carpeting needed for a room. Be sure to use the appropriate units (inches, feet, yards, etc. ) with your answers. 6. 2. 2: CALCULATING PERIMETER AND AREA 3

AREA OF A PARALLELOGRAM 6. 2. 2: CALCULATING PERIMETER AND AREA 4

GUIDED PRACTICE, EXAMPLE 1 Parallelogram ABCD has vertices A (-5, 4), B (3, 4), C (5, -1), and D (-3, -1). Calculate the perimeter and area of parallelogram ABCD. 6. 2. 2: CALCULATING PERIMETER AND AREA 5

EXAMPLE 1, CONTINUED 6. 2. 2: CALCULATING PERIMETER AND AREA 6

EXAMPLE 1, CONTINUED 6. 2. 2: CALCULATING PERIMETER AND AREA 7

EXAMPLE 1, CONTINUED 6. 2. 2: CALCULATING PERIMETER AND AREA 8

EXAMPLE 1, CONTINUED 6. 2. 2: CALCULATING PERIMETER AND AREA 9

EXAMPLE 1, CONTINUED 6. 2. 2: CALCULATING PERIMETER AND AREA 10

EXAMPLE 1, CONTINUED 6. 2. 2: CALCULATING PERIMETER AND AREA 11

AREA OF A TRIANGLE 6. 2. 2: CALCULATING PERIMETER AND AREA 12

GUIDED PRACTICE, EXAMPLE 2 Triangle ABC has vertices A (2, 1), B (4, 5), and C (7, 1). Calculate the perimeter and area of triangle ABC. 6. 2. 2: CALCULATING PERIMETER AND AREA 13

EXAMPLE 2 6. 2. 2: CALCULATING PERIMETER AND AREA 14

EXAMPLE 2, CONTINUED 6. 2. 2: CALCULATING PERIMETER AND AREA 15

EXAMPLE 2, CONTINUED 6. 2. 2: CALCULATING PERIMETER AND AREA 16

EXAMPLE 2, CONTINUED 6. 2. 2: CALCULATING PERIMETER AND AREA 17

EXAMPLE 2, CONTINUED 6. 2. 2: CALCULATING PERIMETER AND AREA 18

AREA OF A TRAPEZOID 6. 2. 2: CALCULATING PERIMETER AND AREA 19

GUIDED PRACTICE, EXAMPLE 3 Trapezoid EFGH has vertices E (-8, 2), F (-4, 2), G (-2, -2), and H (-10, -2). Calculate the perimeter and area of trapezoid EFGH. 6. 2. 2: CALCULATING PERIMETER AND AREA 20

EXAMPLE 3, CONTINUED 6. 2. 2: CALCULATING PERIMETER AND AREA 21

EXAMPLE 3, CONTINUED 6. 2. 2: CALCULATING PERIMETER AND AREA 22

EXAMPLE 3, CONTINUED 6. 2. 2: CALCULATING PERIMETER AND AREA 23

EXAMPLE 3, CONTINUED 6. 2. 2: CALCULATING PERIMETER AND AREA 24

EXAMPLE 3, CONTINUED 6. 2. 2: CALCULATING PERIMETER AND AREA 25

EXAMPLE 3, CONTINUED 6. 2. 2: CALCULATING PERIMETER AND AREA 26

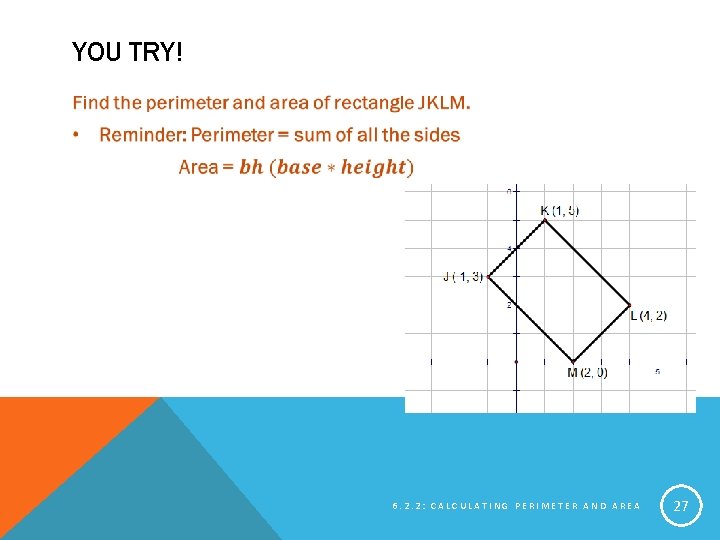
YOU TRY! 6. 2. 2: CALCULATING PERIMETER AND AREA 27

3 -2 -1 3 – List three things you learned from this lesson. 2 – List two things you used in this lesson that you learned in previous lessons. 1 – Write one question you still have about area and perimeter of polygons. 6. 2. 2: CALCULATING PERIMETER AND AREA 28