LESSON 6 1 Identifying and Representing Functions How

LESSON 6. 1 Identifying and Representing Functions How can you identify and represent functions?

Texas Essential Knowledge and Skills The student is expected to: Proportionality— 8. 5. G Identify functions using sets of ordered pairs, tables, mappings, and graphs. Mathematical Processes 8. 1. E Create and use representations to organize, record, and communicate mathematical ideas.

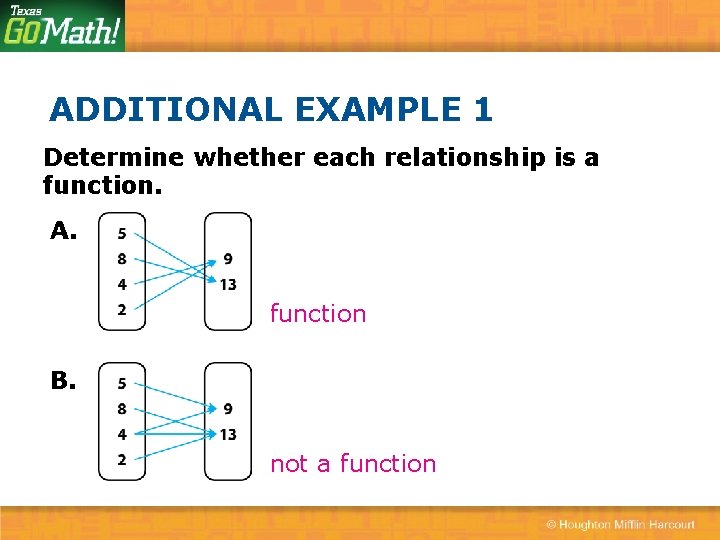
ADDITIONAL EXAMPLE 1 Determine whether each relationship is a function. A. function B. not a function

ADDITIONAL EXAMPLE 2 Determine whether each relationship is a function. A. not a function B. function

ADDITIONAL EXAMPLE 3 The graph shows the relationship between the width of a sticker and the length of the sticker sold at an art store. Is the relationship represented by the graph a function? Explain why. Yes; for each x-value, there is only one y-value.

6. 1 LESSON QUIZ 8. 5. G 1. There are 12 iron-on patches in 4 packages. Each package has the same number of patches. Write a rule in words for the number of packages Leah needs to buy to get x patches. Then write the rule as an algebraic expression. Divide the number of patches by 3;

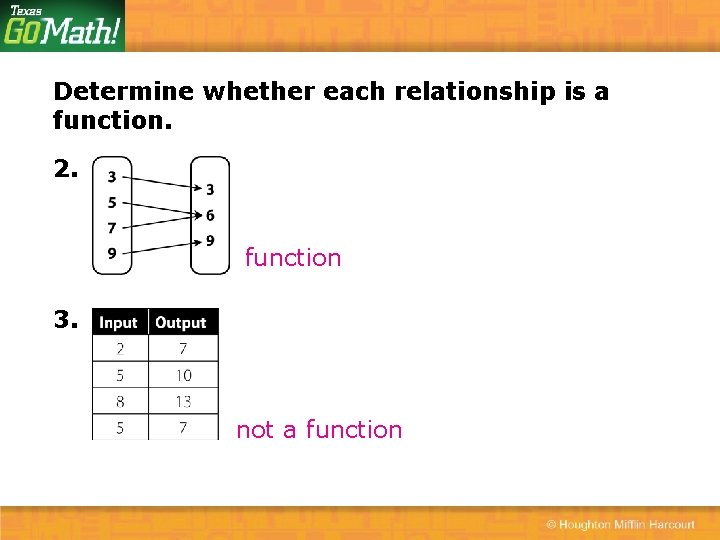
Determine whether each relationship is a function. 2. function 3. not a function

Determine whether each relationship is a function. 4. The graph shows the relationship between the number of texts a person sends and the number of hours the person spends outside during the summer. Is the relationship represented by the graph a function? Explain. No; at least one of the input values is paired with more than one output value; in fact, many of the input values are paired with more than one output value.

The inverse of a relationship is found by switching the coordinates in each ordered pair of the relationship. So, for each ordered pair (x, y) in the relationship, the ordered pair (y, x) will appear in its inverse. Graph the function {(1, 3), (2, 4), (3, 5), (– 1, 1), (– 3, – 1)}, find its inverse, and graph the inverse. Is the inverse of this function a function? Try to find a counterexample to determine whether the inverse of a function is always a function.

Inverse of the function: {(3, 1), (4, 2), (5, 3), (1, 1), (– 3, – 1)}; yes, the inverse of the function is a function. Sample answer (counterexample): function: {(5, 2), (7, 2), (– 3, 1), (– 5, 0)}; inverse of the function: {(2, 5), (2, 7), (1, – 3), (0, – 5)}; the inverse is not a function. So, the inverse of a function is not always a function.

How can you identify and represent functions? Sample answer: Some ways to represent a function are a mapping diagram, a table, a graph, and ordered pairs. To determine whether a relationship is a function, check that each input value is matched with only one output value.