Lesson 58 Congruence Angle Side AAS SSS and

Lesson #58 Congruence: Angle, Side (AAS) SSS and SAS 4 -4 Triangle 4 -5 AAS Do Now: Take out HW Tonight’s HW # 58 Big Ideas: Page 274 # 1 -5, 8, 10 -12, 16, 19, 20, 24, 26 Holt Geometry

Page 267 ASAand SAS Congruence: SSS 4 -4 Triangle 4 -5 (S) (S) Holt Geometry

Page 274 Congruence: SSS and SAS 4 -4 Triangle 4 -5 AAS Holt Geometry

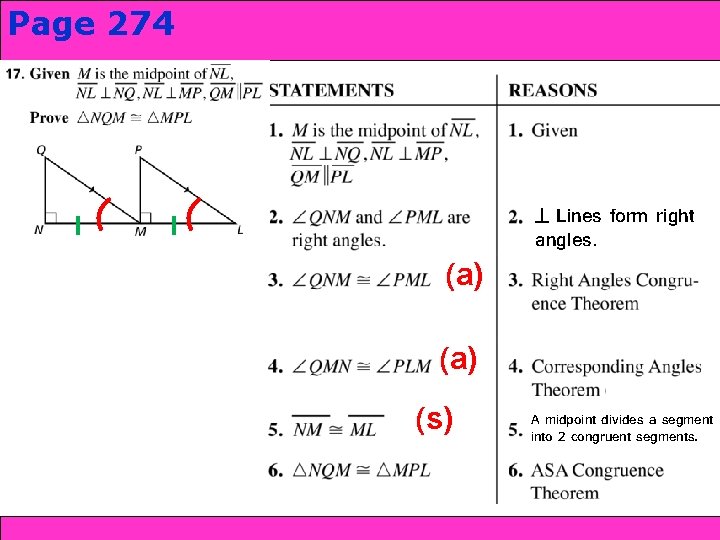
Page 274 Congruence: SSS and SAS 4 -4 Triangle 4 -5 AAS (a) Lines form right angles. (a) (s) Holt Geometry A midpoint divides a segment into 2 congruent segments.

Page 274 Congruence: SSS and SAS 4 -4 Triangle 4 -5 AAS (a)(a) 2. JK 3. AJ + JK CK + JK 4. AK CJ (s) 5. ABK CBJ Holt Geometry 2. Reflexive Postulate 3. Addition Postulate 4. Substitution Postulate 5. ASA

and SAS 4 -4 Triangle Congruence: SSS 4 -5 ASA So far we have learned 3 postulates for proving triangles congruent: SSS SAS ASA Holt Geometry

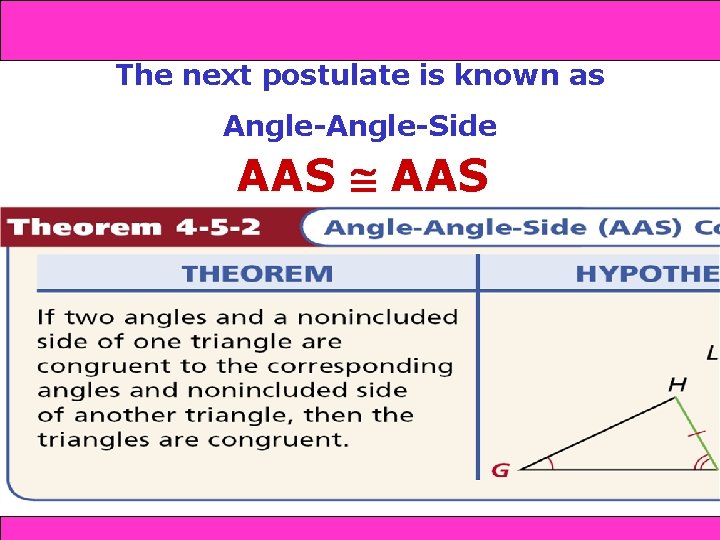
and SAS 4 -4 Triangle Congruence: SSS 4 -5 AAS The next postulate is known as Angle-Side AAS Holt Geometry

and SAS 4 -4 Triangle Congruence: SSS 4 -5 AAS Theorem If 2 angles and a non -included side of one triangle are congruent to the corresponding angles and non-included side of another triangle, the triangles are congruent Holt Geometry

and SAS 4 -4 Triangle Congruence: SSS 4 -5 AAS YOU NOW HAVE FOUR “SHORTCUTS” FOR PROVING TWO TRIANGLES CONGRUENT Holt Geometry

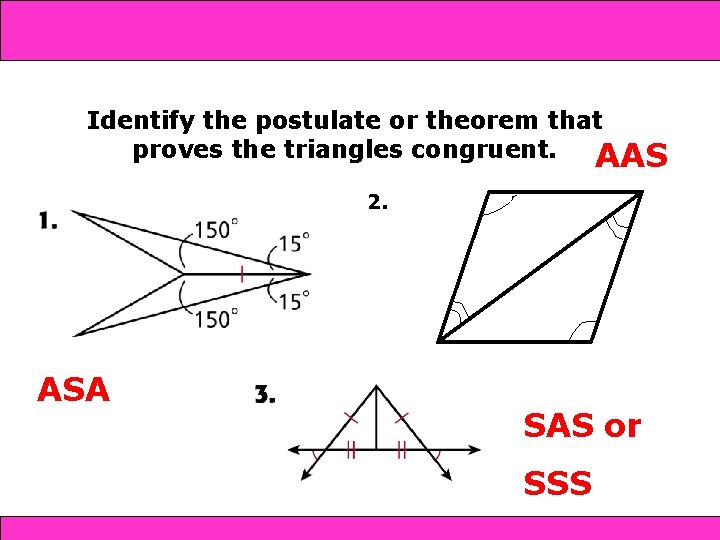
and SAS 4 -4 Triangle Congruence: SSS 4 -5 AAS Identify the postulate or theorem that proves the triangles congruent. AAS 2. ASA SAS or SSS Holt Geometry

and SAS 4 -4 Triangle Congruence: SSS 4 -5 AAS TWO TRIANGLES cannot BE PROVED CONGRUENT BY: AAA OR ASS SSA Also known as the “Donkey” Theorem SSA Holt Geometry

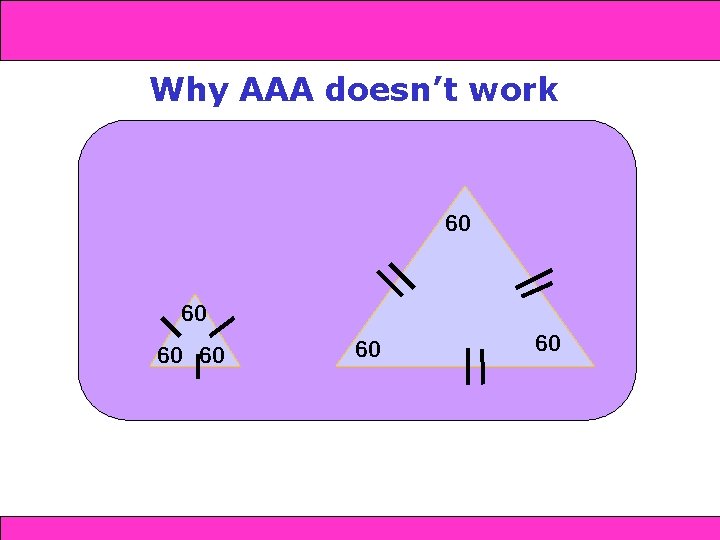
and SAS 4 -4 Triangle Congruence: SSS 4 -5 AAS Why AAA doesn’t work 60 60 Holt Geometry 60 60

and SAS 4 -4 Triangle Congruence: SSS 4 -5 AAS Why the Donkey Theorem doesn’t work Click Here Holt Geometry

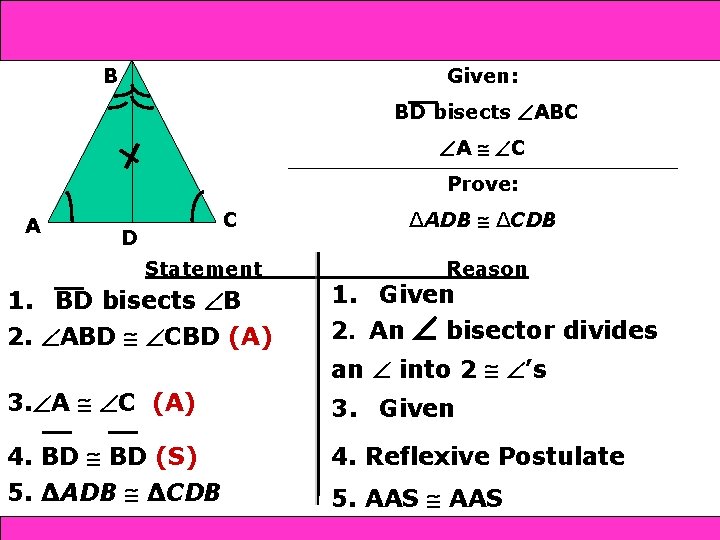
and SAS 4 -4 Triangle Congruence: SSS 4 -5 ASA B Given: BD bisects ABC A C Prove: A C D Statement 1. BD bisects B 2. ABD CBD (A) ∆ADB ∆CDB Reason 1. Given 2. An bisector divides an into 2 ’s 3. A C (A) 3. Given 4. BD (S) 5. ∆ADB ∆CDB 4. Reflexive Postulate Holt Geometry 5. AAS

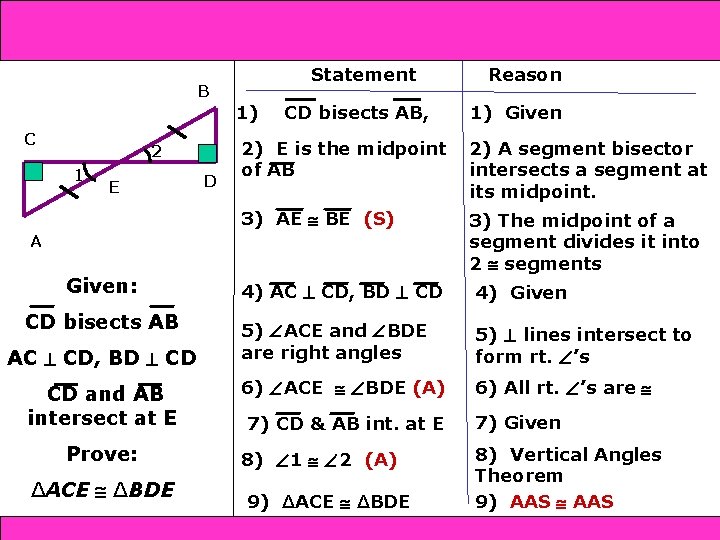
and SAS 4 -4 Triangle Congruence: SSS 4 -5 ASA B C 2 1 E D Statement 1) CD bisects AB, CD bisects AB AC CD, BD CD CD and AB intersect at E Prove: ∆ACE ∆BDE Holt Geometry 1) Given 2) E is the midpoint of AB 2) A segment bisector intersects a segment at its midpoint. 3) AE BE (S) 3) The midpoint of a segment divides it into 2 segments A Given: Reason 4) AC CD, BD CD 4) Given 5) ACE and BDE are right angles 5) lines intersect to form rt. ’s 6) ACE BDE (A) 6) All rt. ’s are 7) CD & AB int. at E 8) 1 2 (A) 9) ∆ACE ∆BDE 7) Given 8) Vertical Angles Theorem 9) AAS

and SAS 4 -4 Triangle Congruence: SSS 4 -5 ASA Homework #58 Big Ideas: Page 274 # 1 -5, 8, 10 -12, 16, 19, 20, 24, 26 Holt Geometry