Lesson 57 Congruence Angle Side Angle ASA Triangle

Lesson 57 Congruence: Angle, Side, Angle (ASA) Triangle SSS and SAS 4 -4 4 -5 ASA Warm Up B C Given: BA AD, CD AD AB DC Prove: A D Statement Reason 1) BA AD, CD AD 1) Given 2) BAD & CDA are right angles 3) BAD CDA (A) 2) Perpendicular lines intersect to form right angles 3) All right angles are congruent 4) Given 5) Reflexive POSTULATE 4) AB DC (S) 5) AD DA (S) 6) ∆ABD ∆DCA Holt Geometry ∆ABD ∆DCA 6) SAS

and SAS 4 -4 Triangle Congruence: SSS 4 -5 ASA Page 260 Holt Geometry

and SAS 4 -4 Triangle Congruence: SSS 4 -5 ASA Holt Geometry

and SAS 4 -4 Triangle Congruence: SSS 4 -5 ASA (S) (A) Holt Geometry

and SAS 4 -4 Triangle Congruence: SSS 4 -5 ASA (S)(A) (S) Holt Geometry

and SAS 4 -4 Triangle Congruence: SSS 4 -5 ASA Holt Geometry

and SAS 4 -4 Triangle Congruence: SSS 4 -5 ASA Holt Geometry

and SAS 4 -4 Triangle Congruence: SSS 4 -5 ASA (S) (A) (S) Holt Geometry

and SAS 4 -4 Triangle Congruence: SSS 4 -5 ASA So far, we have used 2 “shortcuts” for proving triangles For example, you only need to know that two triangles have three pairs of congruent corresponding sides. SSS You were also able to prove two triangles congruent using two pairs of congruent corresponding sides AND congruent corresponding included angles. SAS Holt Geometry

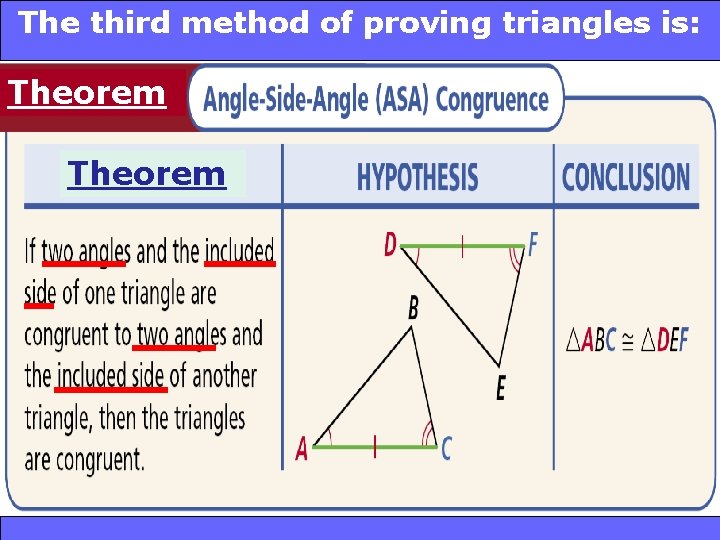
The method of proving triangles Triangle Congruence: SSS and SAS is: 4 -4 third 4 -5 ASA Theorem Holt Geometry

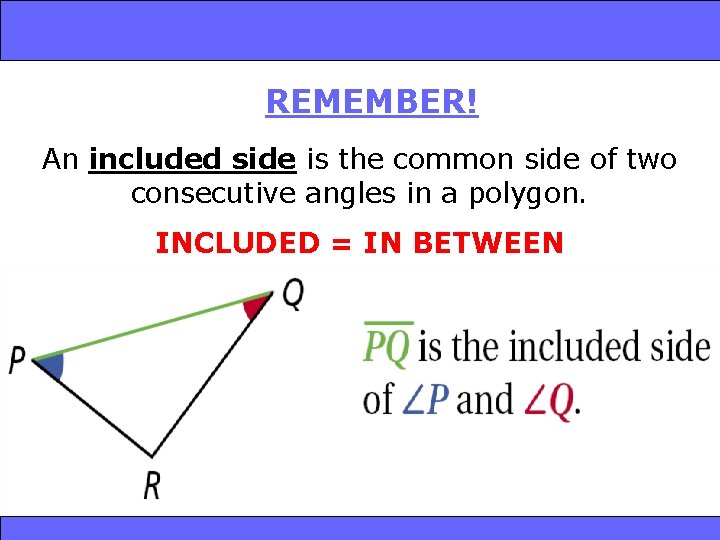
and SAS 4 -4 Triangle Congruence: SSS 4 -5 ASA REMEMBER! An included side is the common side of two consecutive angles in a polygon. INCLUDED = IN BETWEEN Holt Geometry

and SAS 4 -4 Triangle Congruence: SSS 4 -5 ASA Congruence Theorem If 2 angles and the included side of one triangle are congruent to the 2 corresponding angles and included side of another triangle, the triangles are congruent Holt Geometry

and SAS 4 -4 Triangle Congruence: SSS 4 -5 ASA Given: B AEB & CED are right angles AE CE, A DCE C Prove: E A D 1. Statement AEB & CED are right angles 2. AEB CED (A) 3. AE CE (S), A DCE (A) 4. ∆ABE ∆CDE Holt Geometry ∆ABE ∆CDE Reason 1. Given 2. All right angles are 3. Given 4. ASA

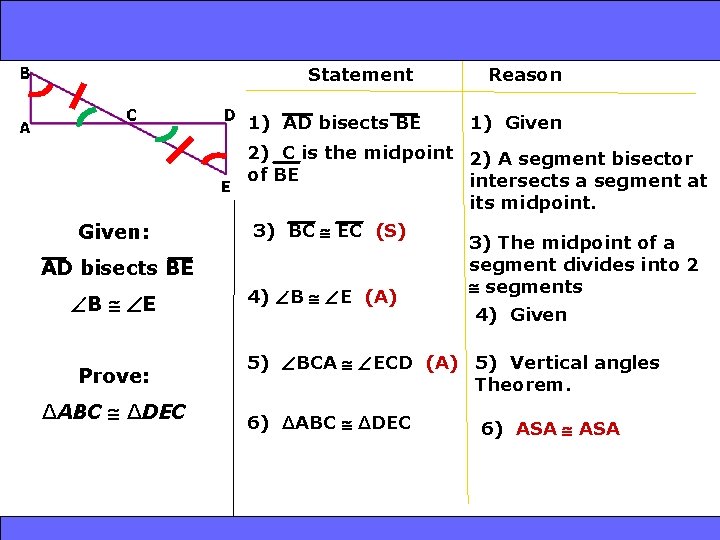
and SAS 4 -4 Triangle Congruence: SSS 4 -5 ASA Statement 1) AD bisects BE Reason 1) Given 2) C is the midpoint 2) A segment bisector of BE intersects a segment at its midpoint. Given: 3) BC EC (S) AD bisects BE B E Prove: ∆ABC ∆DEC Holt Geometry 4) B E (A) 3) The midpoint of a segment divides into 2 segments 4) Given 5) BCA ECD (A) 5) Vertical angles Theorem. 6) ∆ABC ∆DEC 6) ASA

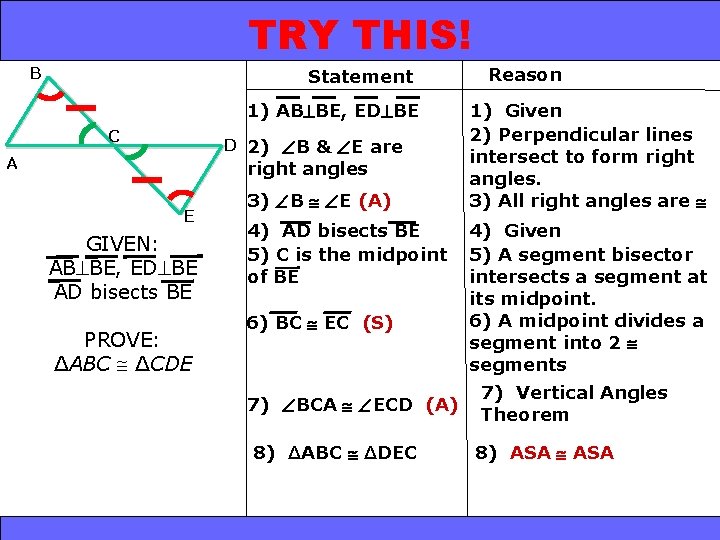
SSS and SAS 4 -4 Triangle Congruence: 4 -5 ASA TRY THIS! B Statement 1) AB BE, ED BE C D 2) B & E are A right angles E GIVEN: AB BE, ED BE AD bisects BE PROVE: ∆ABC ∆CDE 3) B E (A) 4) AD bisects BE 5) C is the midpoint of BE 6) BC EC (S) 7) BCA ECD (A) 8) ∆ABC ∆DEC Holt Geometry Reason 1) Given 2) Perpendicular lines intersect to form right angles. 3) All right angles are 4) Given 5) A segment bisector intersects a segment at its midpoint. 6) A midpoint divides a segment into 2 segments 7) Vertical Angles Theorem 8) ASA

SSS and SAS 4 -4 Triangle Congruence: 4 -5 ASA HW #57 Big Ideas p. 267 #16 Read pages 270 -272 Do page 274 -275 #6, 8, 15, 17 & 18 Hint: For #’s 16 & 18 Use the Addition Postulate followed by the Substitution Postulate to add segments. Holt Geometry