Lesson 56 Finding angles of rotation Angles of

Lesson 56 Finding angles of rotation

Angles of rotation § An angle is said to be in standard position when its vertex is at the origin and one ray is on the positive x-axis. § The terminal side of the angle is the ray of the angle that is rotated relative to the x-axis. § The initial side of the § angle is located directly § on the x-axis.

Angle of rotation § An angle formed by rotating the terminal side and keeping the initial side in place is called an angle of rotation. § The terminal side can be rotated more than 360 o

Drawing angles in standard position § § § § § Draw each angle in standard position. 45 60 135 190 250 -225 440 -125 380

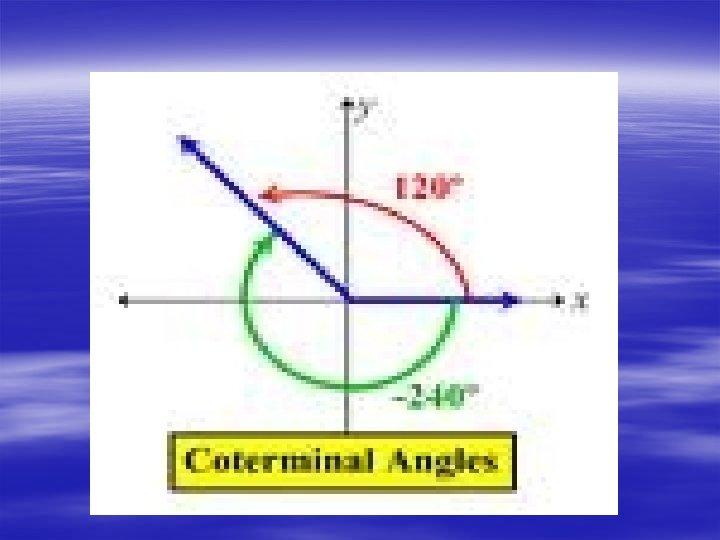
Coterminal angles § Coterminal angles are angles that share the terminal side. § For example: the angles 90 and 450 are coterminal § Positive and negative angles can also be coterminal § For example: 45 is coterminal to the angle 315 § The number of coterminal angles is infinite

Finding the measures of coterminal angles § Find the measure of 1 positive and one negative coterminal angle to a 68 o angle. § To find a positive coterminal angle , add 360 o 68+360= 428 § To find the negative coterminal angle subtract 360 o 68 -360 = -292 § Find a positive and negative coterminal angle to 515 o

practice § Find the measures of 1 positive and 1 negative coterminal angle to : § § 54 o 32 o 475 o -225 o

To find reference angles § § In Quadrant I- the angle itself In Quadrant II - 180 In Quadrant III- - 180 In Quadrant IV- 360 -

Find the measure of the reference angle for the given angles § = 155 § = 240 § = -20 § = 115 § = 225 § = -55

Trigonometric functions § Angles in standard position and reference angles can be used to find the value of trigonometric functions for an angle with measurement § The distance r from a point Q with coordinates (x, y) located on the terminal side of the angle to the origin is given by

Trig functions § For a point Q(x, y) on the terminal side of § in standard position and

Finding values of trig functions § Point Q is located on the terminal side of angle and has coordinates(-5, 12). Find the exact value of the 6 trig functions for § Step 1: plot point Q and draw the angle in standard form § Step 2: find the value of r § Step 3: Use the values of x, y, and r to find the values of the sine, cosine, and tangent § Step 4: use reciprocals to find csc, sec, and cot

practice § Point Q is located on the terminal side of angle and has coordinates (6, 8). Find the exact values of the 6 trig functions

Reference angles § An angle with measurement in standard position forms an angle with the x-axis § The acute angle formed by the terminal side of the angle of rotation and the x-axis is called the reference angle § Reference angles always measure less than 90 o

Lab 9 §Using the trig keys and adjusting to a trig window

§ A graphing calculator can be used to calculate and graph trig functions in both degrees and radians. § A radian is a unit of measurement calculated by dividing the arc length of a central angle by the radius of the circle

Degree mode § Change MODE to DEGREE and press ENTER. § Any trig functions calculated will be in degrees § To find sin 45 o, press SIN 45) ENTER § Answer should be. 7071067812

Radian mode § While the calculator is in radian mode, it will assume the input is radians. § If you press sin 45, while it is in radian mode it will assume you want the sin 45 radians § You will get an answer of. 8509035245 § Radian mode must always be used to graph trig functions to obtain an accurate graph

Adjusting to a trig window § ZOOM Trig will give you an acceptable window for graphing most trig functions. § But you should be able to create a window by changing the Window variables in your calculator § Xmin= -2 pi § Xmax = 2 pi § Xscale = pi/2 § Ymin = -2 § Ymax = 2 § Yscale = 1

Do lab practice p. 371