lesson 5 ELECTRON IN 1 D POTENTIAL Electrons

lesson #5: ELECTRON IN 1 D POTENTIAL Electrons in a 1 D periodical potential Solid State Physics M. Casalboni 2018/’ 19 Outline: The Bloch theorem Tight binding approximation Plane waves and nearly free electrons Band theory Dyamical aspects Zurich 1905 -1983 Nobel in 1952 1/18

lesson #5: ELECTRON IN 1 D POTENTIAL Solid State Physics M. Casalboni 2018/’ 19 Let we recall some statements of Quantum Mechanics: In Quantum Mechanics «observables» can be measured. They and the values so obtained are connected by the Schroedringer equation. The most important observable of a system is the Energy and the Schrödringer equation for such a quantity reads: HΨ=EΨ 2/18

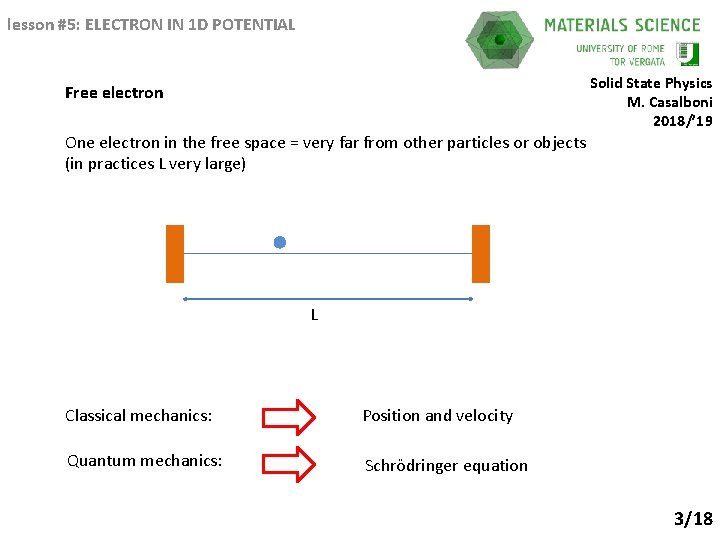
lesson #5: ELECTRON IN 1 D POTENTIAL Solid State Physics M. Casalboni 2018/’ 19 Free electron One electron in the free space = very far from other particles or objects (in practices L very large) L Classical mechanics: Position and velocity Quantum mechanics: Schrödringer equation 3/18

lesson #5: ELECTRON IN 1 D POTENTIAL Free electron Solid State Physics M. Casalboni 2018/’ 19 One electron in the free space = very far from other particles or objects (in practices L very large) 4/18

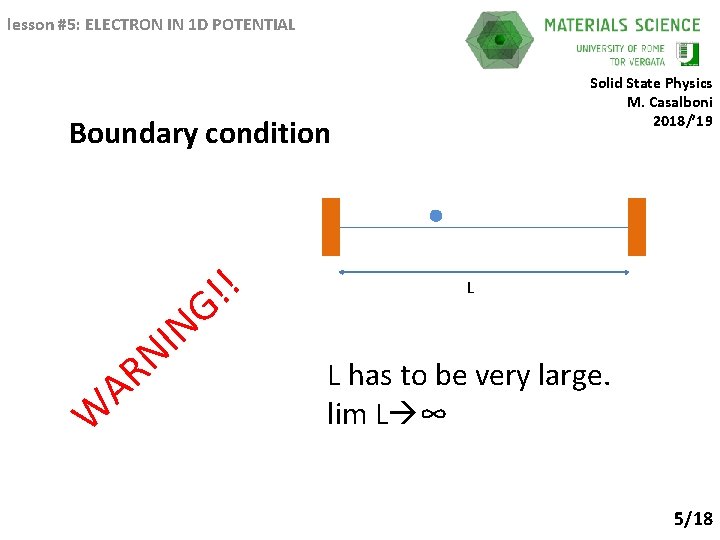
lesson #5: ELECTRON IN 1 D POTENTIAL Solid State Physics M. Casalboni 2018/’ 19 Boundary condition N I N W R A ! ! G L L has to be very large. lim L ∞ 5/18

lesson #5: ELECTRON IN 1 D POTENTIAL Solid State Physics M. Casalboni 2018/’ 19 For describing crystals we are interested to PERIODICAL potentials 6/18

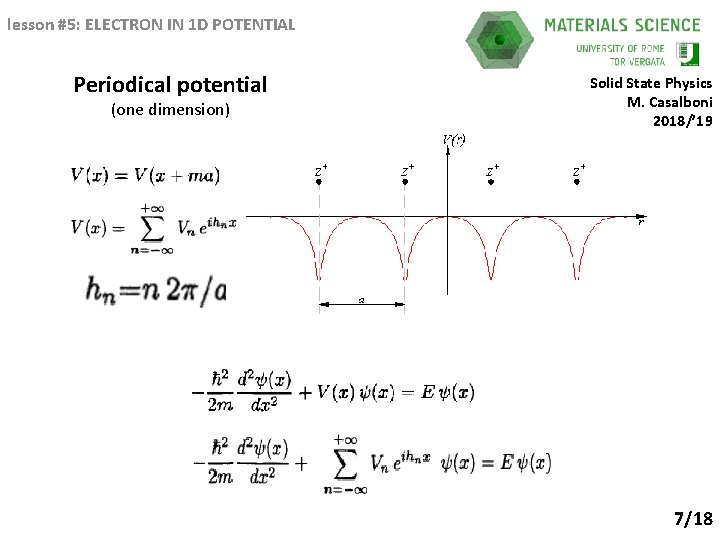
lesson #5: ELECTRON IN 1 D POTENTIAL Periodical potential (one dimension) Solid State Physics M. Casalboni 2018/’ 19 7/18

lesson #5: ELECTRON IN 1 D POTENTIAL Let we see what appens if we apply this hamiltonian to a single plane wave Solid State Physics M. Casalboni 2018/’ 19 will give only terms depending on 8/18

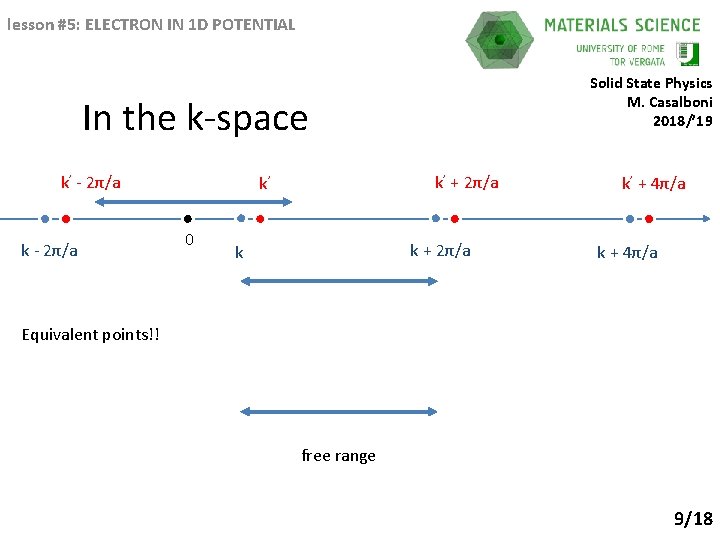
lesson #5: ELECTRON IN 1 D POTENTIAL Solid State Physics M. Casalboni 2018/’ 19 In the k-space k’ - 2π/a k’ + 2π/a k’ 0 k + 2π/a k k’ + 4π/a k + 4π/a Equivalent points!! free range 9/18

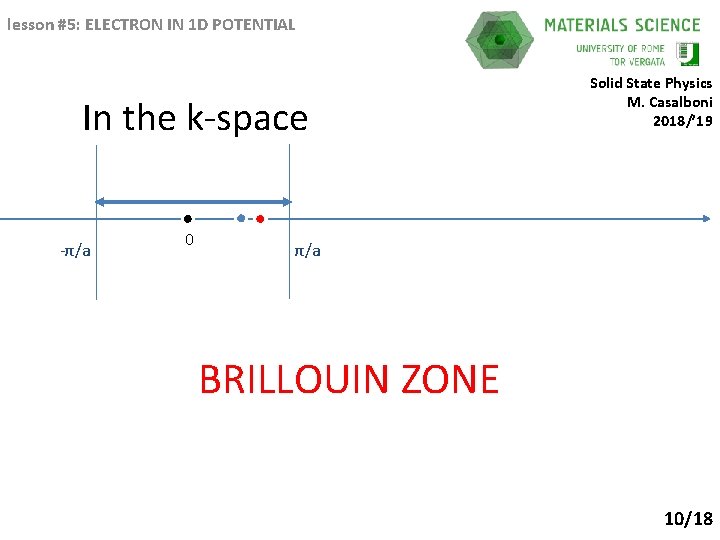
lesson #5: ELECTRON IN 1 D POTENTIAL In the k-space -π/a 0 Solid State Physics M. Casalboni 2018/’ 19 π/a BRILLOUIN ZONE 10/18

lesson #5: ELECTRON IN 1 D POTENTIAL Returning to the Solid State Physics M. Casalboni 2018/’ 19 m e r o e h t H C O L B . It has the same periodicity of the lattice 11/18

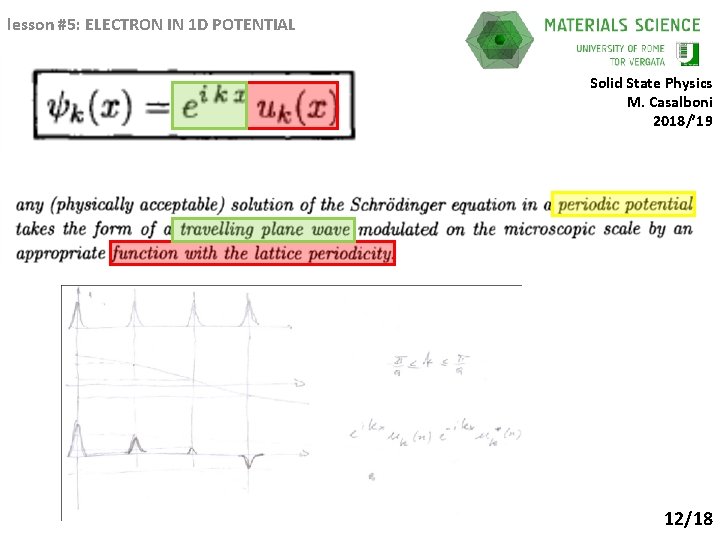
lesson #5: ELECTRON IN 1 D POTENTIAL Solid State Physics M. Casalboni 2018/’ 19 12/18

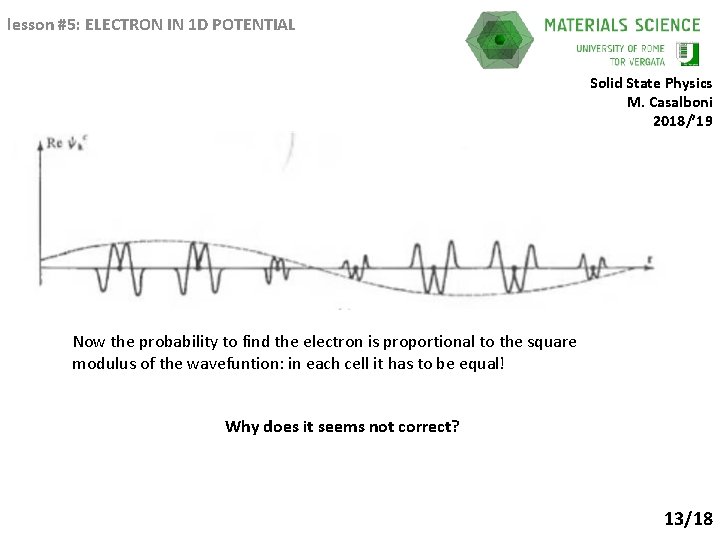
lesson #5: ELECTRON IN 1 D POTENTIAL Solid State Physics M. Casalboni 2018/’ 19 Now the probability to find the electron is proportional to the square modulus of the wavefuntion: in each cell it has to be equal! Why does it seems not correct? 13/18

lesson #5: ELECTRON IN 1 D POTENTIAL Solid State Physics M. Casalboni 2018/’ 19 14/18

lesson #5: ELECTRON IN 1 D POTENTIAL Solid State Physics M. Casalboni 2018/’ 19 15/18

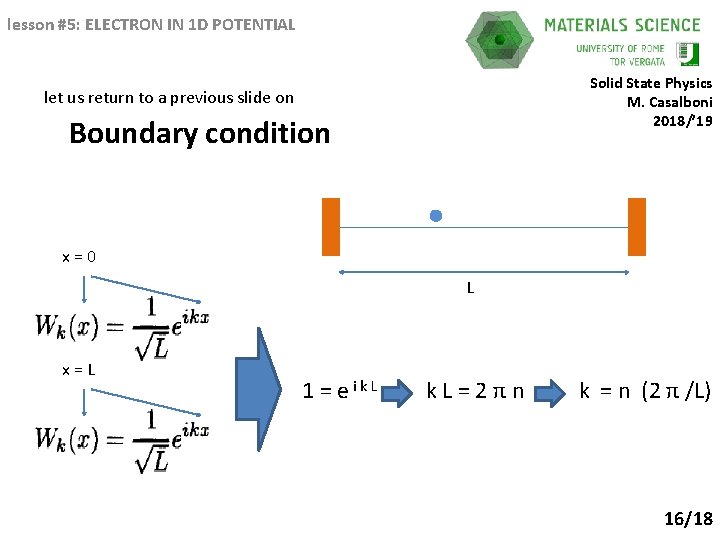
lesson #5: ELECTRON IN 1 D POTENTIAL Solid State Physics M. Casalboni 2018/’ 19 let us return to a previous slide on Boundary condition x=0 L x=L 1 = eik. L=2πn k = n (2 π /L) 16/18

lesson #5: ELECTRON IN 1 D POTENTIAL Solid State Physics M. Casalboni 2018/’ 19 BOUNDARY CONDITIONS As done above 17/18

lesson #5: ELECTRON IN 1 D POTENTIAL Solid State Physics M. Casalboni 2018/’ 19 18/18