Lesson 5 4 Objective To identify three types

Lesson 5. 4 Objective: To identify three types of linear systems. EQ: How can you tell the number of solutions of a system of equations? The 3 kinds of systems 1) Regular system. When the two lines intersect once. One solution 2) No Solution. When the lines never intersect (Parallel) No solutions 3) Coinciding lines. The two equations form the same line on top of each other. The same line. Every point that is true for one line is true for the other Infinite number of solutions

Samples One solution where the lines cross No solution the lines are parallel Inconsistent The lines coincide. All points that are true for one line are also true for the other. Many solutions Dependent

Example: Solve the system if possible 2 x + 2 y = 4 -x - y = -2 2 x + 2 y = 4 2(-x - y = -2) Everything cancels Multiply by 2 2 x + 2 y = 4 -2 x – 2 y = -4 0=0 These equations represent the same line. The system has an infinite number of solutions.

Example Solve if possible -x + y = 7 2 x – 2 y = -18 2(-x + y = 7) 2 x – 2 y = -18 Multiply by 2 -2 x + 2 y = 14 2 x – 2 y = -18 0 = – 4 False ! No Solution These equations represent parallel lines
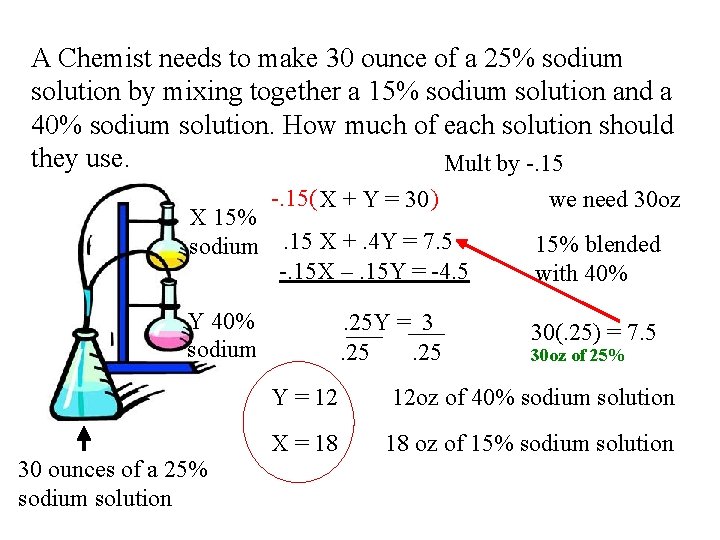
A Chemist needs to make 30 ounce of a 25% sodium solution by mixing together a 15% sodium solution and a 40% sodium solution. How much of each solution should they use. Mult by -. 15( X + Y = 30 ) X 15% sodium. 15 X +. 4 Y = 7. 5 -. 15 X –. 15 Y = -4. 5 Y 40% sodium 30 ounces of a 25% sodium solution . 25 Y = 3. 25 we need 30 oz 15% blended with 40% 30(. 25) = 7. 5 30 oz of 25% Y = 12 12 oz of 40% sodium solution X = 18 18 oz of 15% sodium solution
- Slides: 5