Lesson 5 4 b Net Change Theorem Icebreaker

Lesson 5 -4 b Net Change Theorem

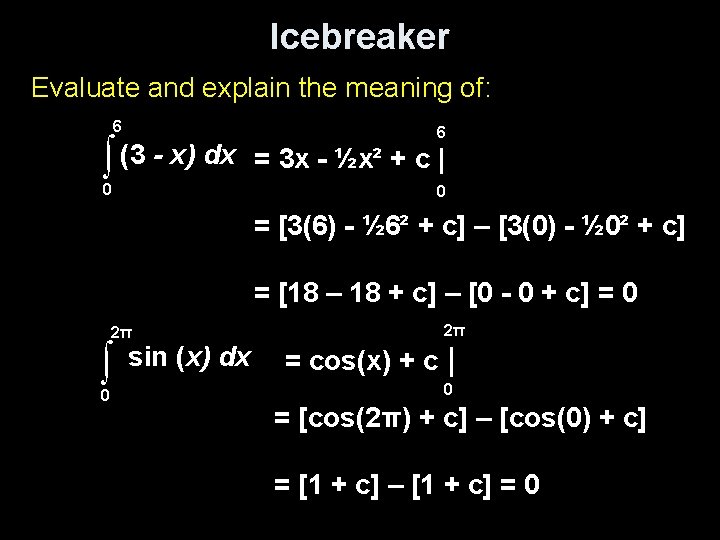
Icebreaker Evaluate and explain the meaning of: 6 ∫ (3 - x) dx 0 6 = 3 x - ½x² + c | 0 = [3(6) - ½ 6² + c] – [3(0) - ½ 0² + c] = [18 – 18 + c] – [0 - 0 + c] = 0 2π ∫ 0 sin (x) dx 2π = cos(x) + c | 0 = [cos(2π) + c] – [cos(0) + c] = [1 + c] – [1 + c] = 0

Objectives • Solve indefinite integrals of algebraic, exponential, logarithmic, and trigonometric functions • Understand the Net Change Theorem • Use integrals to solve distance problems to find the displacement or total distance traveled

Vocabulary • Indefinite Integral – is a function or a family of functions • Distance – the total distance traveled by an object between two points in time • Displacement – the net change in position between two points in time

Example Problems A deer population is increasing at a rate of dp/dt = 20 + 35 t per year (where t is measured in years). By how much does the deer population increase between the 4 th and 10 th years? Show integral set up and answer. 10 P= ∫ (20 + 35 t) dt 4 10 P = 20 t + ½ (35)t² + C | 4 [20(10) + ½ (35)(10)² + C] - [20(4) + ½ (35)(4)² + C] [200 + 1750 + C] - [80 + 280 + C] = 1590 increase in deer

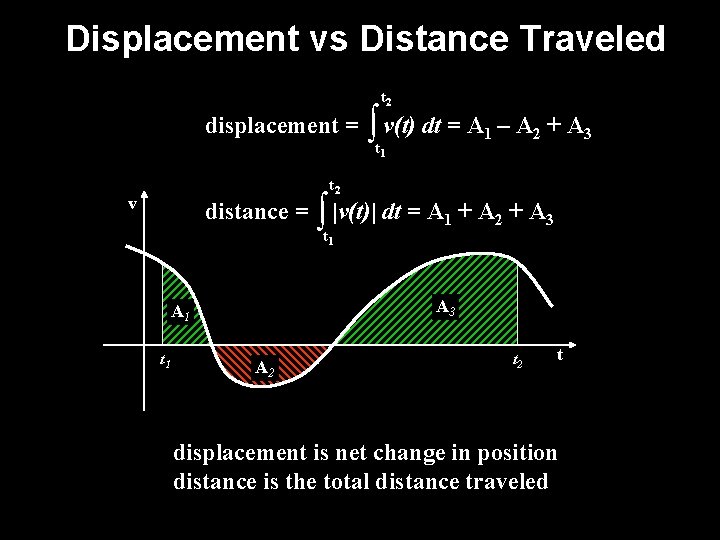
Displacement vs Distance Traveled t 2 displacement = ∫ v(t) dt = A t 1 1 – A 2 + A 3 t 2 v distance = ∫ |v(t)| dt = A t 1 + A 2 + A 3 A 1 t 1 1 A 2 t displacement is net change in position distance is the total distance traveled

Example Problems cont Evaluate: 2 2) ∫ (1 – x²) dx -1 2 = (x – ⅓x³) | = [2 - 8/3] - [1 – 1/3] -1 = [-2/3] - [2/3] = -4/3

Example Problems cont Remember definition of |x| ! Evaluate: ∫ 3) 2 x if x > 0 -x if x < 0 F(x) = |x| = |(1 – x²)| dx -1 (1 – x²) < 0 if x > 1 SO 1 ∫ (1 – x²) dx -1 1 (x – ⅓x³) | -1 2 - ∫(1 – x²) dx 1 2 - (x – ⅓x³) | = [2/3 - -4/3] - [-2/3 – 2/3] 1 [6/3] - [-4/3] = 10/3

Example Problems cont Problem 55 from the book: Given the following: A(t) = t + 4, v(0) = 5, 0 ≤ t ≤ 10 Find the velocity at time t V(t) = ∫ (t + 4) dt = ½t² + C V(0) = 5 = C Find the distance traveled during the given interval 10 S(t) = ∫ (½t² + 5) dt 0 10 = (1/6)t³ + 5 t + C | 0 = (1000/6 + 50 + C) – (C) = 216. 67

Summary & Homework • Summary: – Definite Integrals are a number – Evaluated at endpoints of integration – Indefinite Integrals are antiderivatives • Homework: – Day One: pg 402 -404: 19, 22, 27, 28, – Day Two: pg 402 -404: 3, 7, 9, 61 (see appendix E)