Lesson 5 3 The rational numbers Rational numbers

Lesson 5. 3 The rational numbers

• Rational numbers – set of all numbers which can be expressed in the form a/b, where a and b are integers and b is not zero. • A rational number is reduced to its lowest terms or simplified when the numerator or denominator have no common divisors other than 1.

• Reduce to lowest terms

• Mixed number – the sum of an integer and a rational number. • Improper fraction – a rational number whose numerator is greater than its denominator.

• Convert to an improper fraction. • Write as a mixed number.

• Rational Numbers and Decimals – a decimal that terminates or repeats is a rational number • Terminating Decimal • Repeating Decimal

• Express as a decimal 3/8 5/11 • Expressing terminating decimals as fractions. – Use denominators of 10, 1000, 10000, …. . 0. 7 . 52 . 048

• Express a repeating decimal as a quotient of integers 1. Let n = the repeating decimal 2. Multiply both sides of the equation by 10 if one digit repeats, by 100 if two digits repeat and so on 3. Subtract the equation in step 1 from the equation in step 2 4. Divide both sides of the equation in step 3 by the number in front of n and solve for n.

• Multiplying Rational Numbers • Dividing Rational numbers – Multiply by the reciprocal

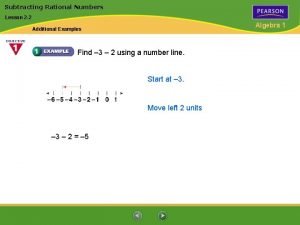
• Adding and subtracting Rational numbers with common denominators. • Adding Rational Numbers with unlike denominators – Find the least common denominator
- Slides: 10