Lesson 5 2 The Definite Integral Ice Breaker

Lesson 5 -2 The Definite Integral

Ice Breaker • Find area between x-axis and y = 2 x on [0, 3] using 3 rectangles and right-end points Area of Rectangle = h ∙ w v 10 xi = a + i∆x RH w = ∆x = (b-a)/n = (3 -0) / 3 = 1 h = f(xi) = 2(xi) R 1 = (2(x 1)) ∙ (∆x) = 2(1) ∙ 1 = 2 R 2 = (2(x 2)) ∙ (∆x) = 2(2) ∙ 1 = 4 t 0 0 5 Area of Triangle = ½ (b)(h) = ½ (3)(6) = 9 R 3 = (2(x 3)) ∙ (∆x) = 2(3) ∙ 1 = 6 RH 1 (2+4+6) = 14

Riemann Sums Let f be a function that is defined on the closed interval [a, b]. If ∆ is a partition of [a, b] and ∆xi is the width of the ith interval, ci, is any point in the subinterval, then the sum n ∑ i=1 f(ci)∆xi is called a Riemann Sum of f. Furthermore, n if exists, lim ∑ n→∞ i=1 f(ci)∆xi The definite integral, b we say f is integrable on [a, b]. ∫a f(x)dx , is the area under the curve
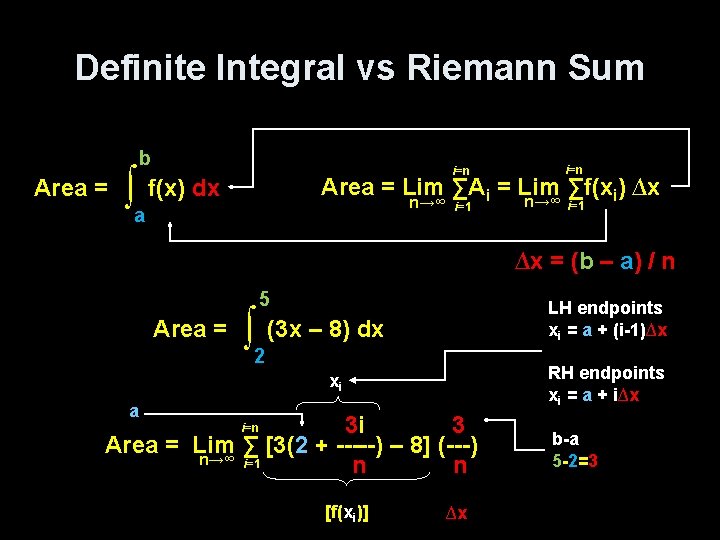
Definite Integral vs Riemann Sum b Area = i=n ∫a f(x) dx Area = Lim ∑Ai = Lim ∑f(xi) ∆x n→∞ i=1 ∆x = (b – a) / n 5 Area = LH endpoints xi = a + (i-1)∆x ∫ 2 (3 x – 8) dx RH endpoints xi = a + i∆x xi a 3 i 3 Area = Lim ∑ [3(2 + -----) – 8] (---) n→∞ i=1 n n i=n [f(xi)] ∆x b-a 5 -2=3

Summary & Homework • Summary: – Riemann Sums are Limits of Infinite sums – Riemann Sums give exact areas under the curve – Riemann Sums are the definite integral • Homework: – pg 390 - 393: 3, 5, 9, 17, 20, 33, 38
- Slides: 5