LESSON 5 1 Writing Linear Equations from Situations








- Slides: 9

LESSON 5. 1 Writing Linear Equations from Situations and Graphs How do you write an equation to model a linear relationship given a graph or a description?

ADDITIONAL EXAMPLE 1 A DJ charges a setup fee plus an hourly fee to provide music for a dance party. Use the graph to write an equation in slope-intercept form to represent the amount spent, y, on x hours of music. y = 75 x + 100

ADDITIONAL EXAMPLE 2 The cost for 25 square yards of carpet is $650 including delivery and installation. The cost for 40 square yards of installed carpet is $950. Write an equation in slope-intercept form for the cost of the installed carpet. y = 20 x + 150

5. 1 LESSON QUIZ 8. 5. I 1. Lee charges $3 for a basket and $2. 50 for each pound of fruit picked at the orchard. Write an equation in y = mx + b form for the total cost of x pounds of fruit from the orchard. y = 2. 50 x + 3

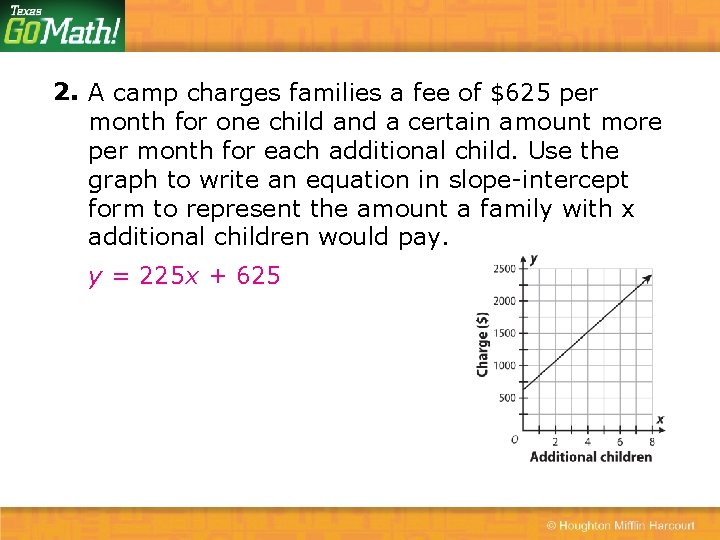
2. A camp charges families a fee of $625 per month for one child and a certain amount more per month for each additional child. Use the graph to write an equation in slope-intercept form to represent the amount a family with x additional children would pay. y = 225 x + 625

3. Identify the y-intercept in question 2 above. Tell what the y-intercept means in this context. b = 625, the fixed fee for one child 4. A driving range charges $4 to rent a golf club plus $2. 75 for every bucket of golf balls you hit. Write an equation that shows the total cost c of hitting b buckets of golf balls. c = 2. 75 b + 4

Give each pair of students a sheet of graph paper marked with the x- and y-axes, and pencils or pieces of wire or spaghetti to use for the lines to make quick graphs. One student calls out a slope (for example, m = 0 or 1, or 0. 5, or -1) and the other places the line on the graph in the approximate position going through the origin, (for example: horizontal, bisecting QI, less steep than y = x, steeper than y = x, or bisecting QII).

Then have one student call out a slope and a y-intercept and the other place the line. If students have trouble, have them place a line with the same slope through the origin and then move it to go through the y-intercept.

How do you write an equation to model a linear relationship given a graph or a description? Use pairs of values for input and output to determine the values for the slope m and the y-intercept b in the equation y = mx + b.