Lesson 5 1 Exponents Growth and Decay Integral













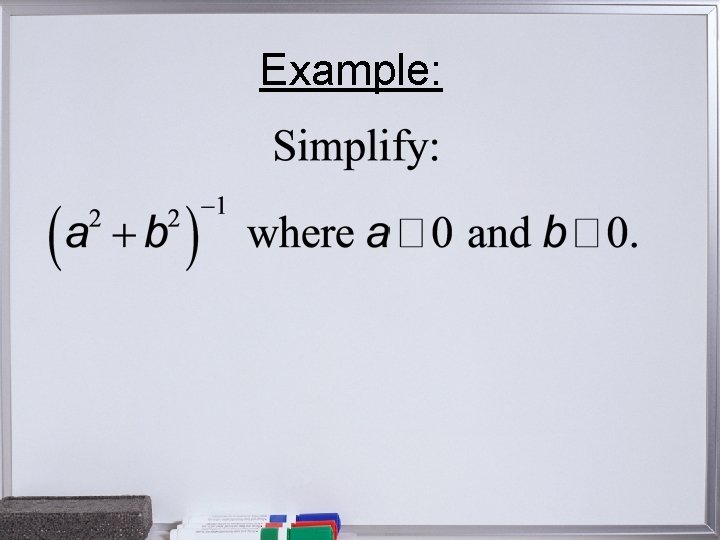
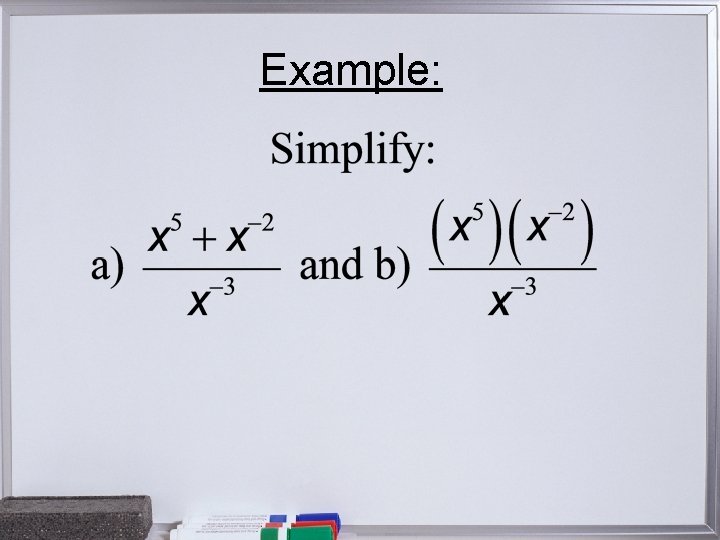















- Slides: 31

Lesson 5 -1 Exponents -Growth and Decay: Integral Exponents

Laws of Exponents:

Laws of Exponents:

Laws of Exponents:

Laws of Exponents:

Laws of Exponents:

Laws of Exponents:

Laws of Exponents:

Laws of Exponents:

Laws of Exponents:

Laws of Exponents:

Example:

Example:
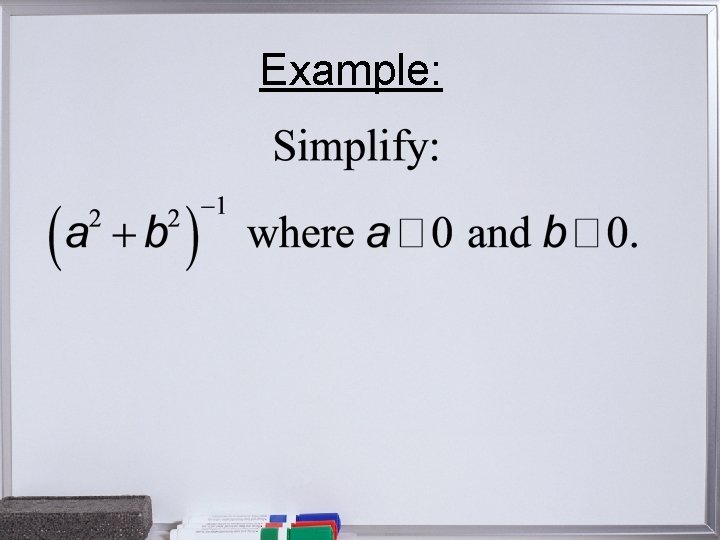
Example:
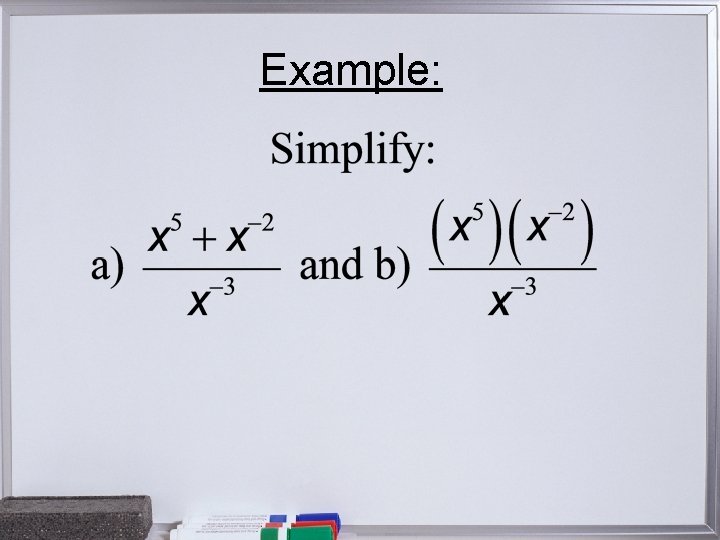
Example:

Suppose that the cost of a hamburger has been increasing at the rate of 9% per year. Then each year the cost is 1. 09 times the cost the previous year. Suppose that the cost now is $4.

Suppose that the cost of a hamburger has been increasing at the rate of 9% per year. Then each year the cost is 1. 09 times the cost the previous year. Suppose that the cost now is $4. Some projected future costs would be:

Suppose that the cost of a hamburger has been increasing at the rate of 9% per year. Then each year the cost is 1. 09 times the cost the previous year. Suppose that the cost now is $4. Some projected future costs would be: Time (years from now) 0 1 2 3 t Cost (dollars) 4 1(4. 09) ? ? ?

Suppose that the cost of a hamburger has been increasing at the rate of 9% per year. Then each year the cost is 1. 09 times the cost the previous year. Suppose that the cost now is $4. Some projected future costs would be: Time (years from now) 0 1 2 3 t Cost (dollars) 4 1(4. 09) ? ? ? The above table suggest that the cost is a function of time t. Since the variable t occurs as an exponent, the cost is said to be an exponential function of time t.

Suppose that the cost of a hamburger has been increasing at the rate of 9% per year. Then each year the cost is 1. 09 times the cost the previous year. Suppose that the cost now is $4. Some projected future costs would be: Time (years from now) 0 1 2 3 t Cost (dollars) 4 1(4. 09) ? ? ? The above table suggest that the cost is a function of time t. Since the variable t occurs as an exponent, the cost is said to be an exponential function of time t. C(t) = ? ?

Using the cost function described earlier, find the cost of a hamburger:

Using the cost function described earlier, find the cost of a hamburger: a) 5 years from now.

Using the cost function described earlier, find the cost of a hamburger: a) 5 years from now. b) 5 years ago.
Using the cost function described earlier, find the cost of a hamburger: a) 5 years from now. b) 5 years ago. Look at the graphs of these two functions. Can you tell which graph describes exponential growth and which graph describes exponential decay?

Generally, all exponential growth or decay problems can be described by this model:

Generally, all exponential growth or decay problems can be described by this model:

Example: Suppose that a radioactive isotope decays so that the radioactivity present decreases 15% per day.

Example: Suppose that a radioactive isotope decays so that the radioactivity present decreases 15% per day. If 40 g are present now, find the amount present:

Example: Suppose that a radioactive isotope decays so that the radioactivity present decreases 15% per day. If 40 g are present now, find the amount present: a) 6 days from now or A(6)=?

Example: Suppose that a radioactive isotope decays so that the radioactivity present decreases 15% per day. If 40 g are present now, find the amount present: a) 6 days from now or A(6)=? b) 6 days ago or A(-6)=?

Assignment: Pgs. 172 – 173 C. E. #1 – 16 all W. E. #1 – 19 odd