Lesson 5 1 Core Focus on Linear Equations

Lesson 5. 1 Core Focus on Linear Equations Scatter Plots and Correlation

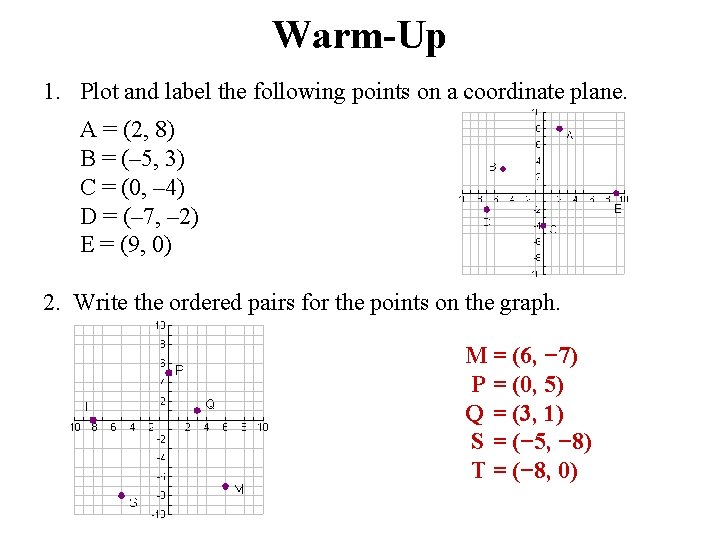
Warm-Up 1. Plot and label the following points on a coordinate plane. A = (2, 8) B = (– 5, 3) C = (0, – 4) D = (– 7, – 2) E = (9, 0) 2. Write the ordered pairs for the points on the graph. M = (6, − 7) P = (0, 5) Q = (3, 1) S = (− 5, − 8) T = (− 8, 0)

Lesson 5. 1 Scatter Plots and Correlation Read, create and describe the correlations in scatter plots.

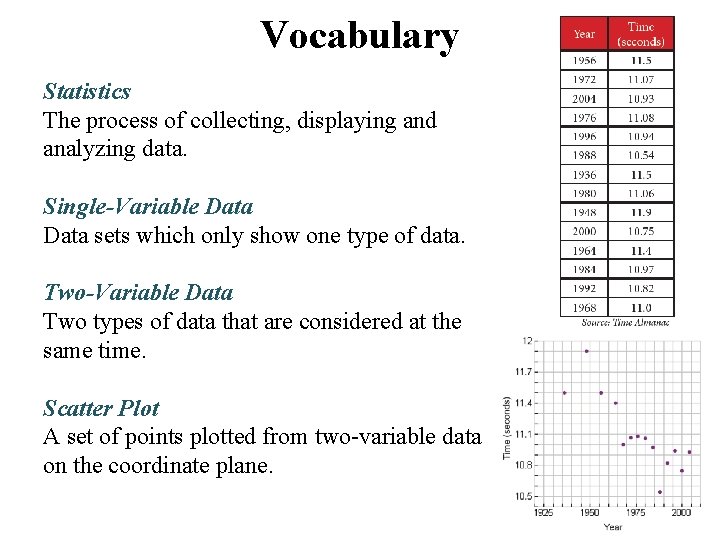
Vocabulary Statistics The process of collecting, displaying and analyzing data. Single-Variable Data sets which only show one type of data. Two-Variable Data Two types of data that are considered at the same time. Scatter Plot A set of points plotted from two-variable data on the coordinate plane.

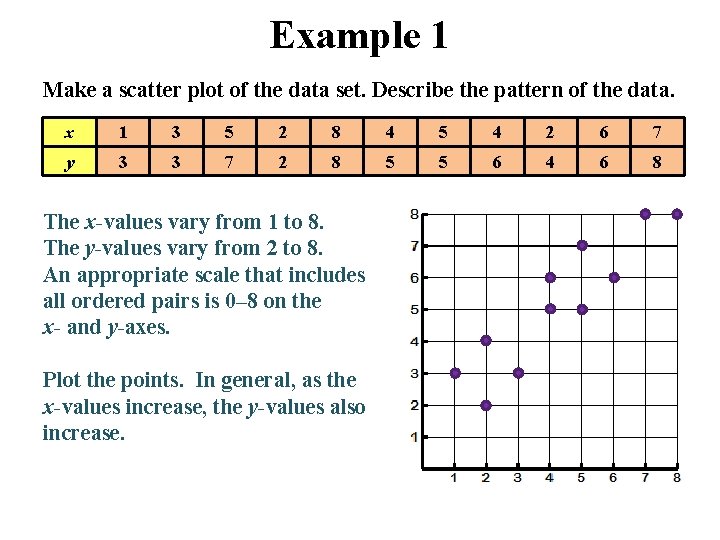
Example 1 Make a scatter plot of the data set. Describe the pattern of the data. x 1 3 5 2 8 4 5 4 2 6 7 y 3 3 7 2 8 5 5 6 4 6 8 The x-values vary from 1 to 8. The y-values vary from 2 to 8. An appropriate scale that includes all ordered pairs is 0– 8 on the x- and y-axes. Plot the points. In general, as the x-values increase, the y-values also increase.

Vocabulary Correlation The relationship between two variables in a scatter plot. Positive Correlation As x increases, y increases. Negative Correlation As x increases, y decreases. No Correlation x and y are not related. Good to Know! Correlations are not always perfect patterns. A correlation shows the general pattern or trend of the data.

Example 2 Predict whether the following sets of data would show a positive, negative or no correlation. Explain. a. a student’s grade level and the amount of recess time Negative. As students get older, the amount of time they get for recess typically decreases. b. a student’s height and their score on the last science test No correlation. The height of a student should have no effect on how they performed on the last science test. c. a student’s height and their shoe size Positive. Shorter students are more likely to have smaller feet and taller students are more likely to have larger feet.

Communication Prompt Describe a real-world situation that would have a positive correlation. Also, describe a situation that would have a negative correlation.

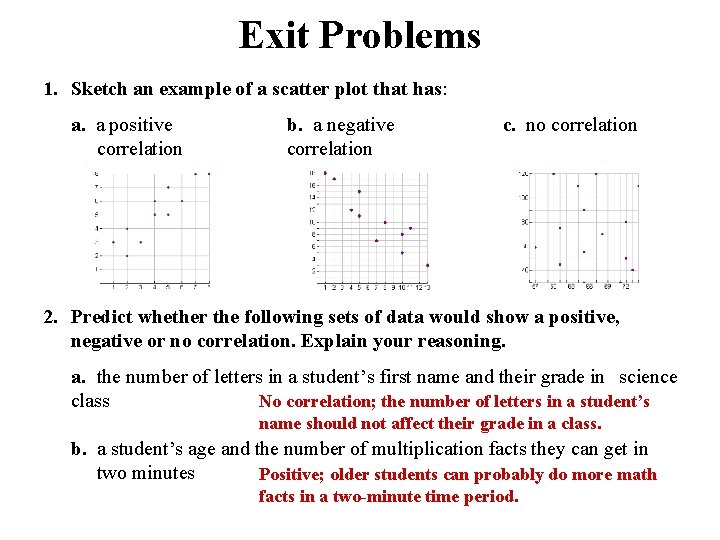
Exit Problems 1. Sketch an example of a scatter plot that has: a. a positive correlation b. a negative correlation c. no correlation 2. Predict whether the following sets of data would show a positive, negative or no correlation. Explain your reasoning. a. the number of letters in a student’s first name and their grade in science class No correlation; the number of letters in a student’s name should not affect their grade in a class. b. a student’s age and the number of multiplication facts they can get in two minutes Positive; older students can probably do more math facts in a two-minute time period.