Lesson 42 Review of Right Triangle Trigonometry Math

Lesson 42 - Review of Right Triangle Trigonometry Math 2 Honors – Santowski Math 2 Honors - Santowski 1

(A) Review of Right Triangle Trigonometry is the study and solution of Triangles. Solving a triangle means finding the value of each of its sides and angles. The following terminology and tactics will be important in the solving of triangles. n Pythagorean Theorem (a 2+b 2=c 2). Only for right angle triangles n Sine (sin), Cosecant (csc or 1/sin) n Cosine (cos), Secant (sec or 1/cos) n Tangent (tan), Cotangent (cot or 1/tan) n Right/Oblique triangle Math 2 Honors - Santowski 2

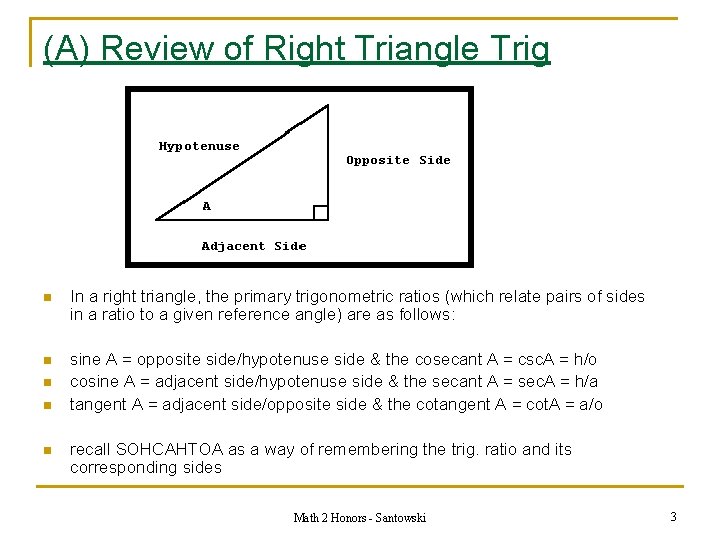
(A) Review of Right Triangle Trig n In a right triangle, the primary trigonometric ratios (which relate pairs of sides in a ratio to a given reference angle) are as follows: n sine A = opposite side/hypotenuse side & the cosecant A = csc. A = h/o cosine A = adjacent side/hypotenuse side & the secant A = sec. A = h/a tangent A = adjacent side/opposite side & the cotangent A = cot. A = a/o n n n recall SOHCAHTOA as a way of remembering the trig. ratio and its corresponding sides Math 2 Honors - Santowski 3

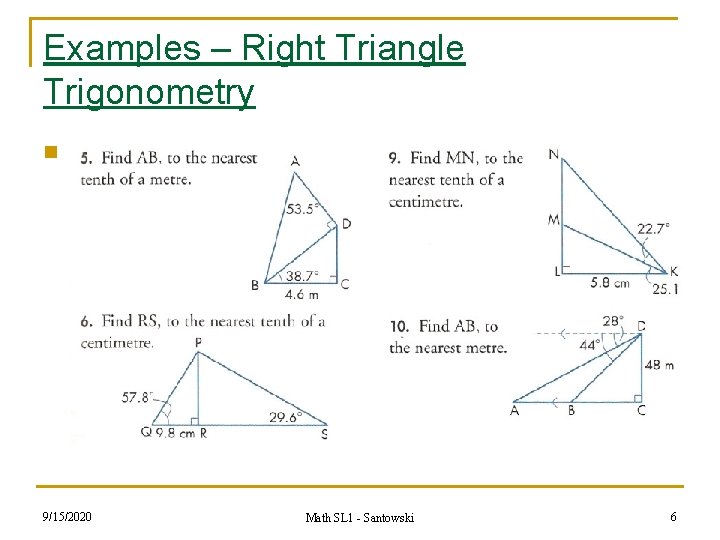
(B) Examples – Right Triangle Trigonometry n Using the right triangle trig ratios, we can solve for unknown sides and angles: n ex 1. Find a in ABC if b = 2. 8, C = 90°, and A = 35° n ex 2. Find A in ABC if c = 4. 5 and a = 3. 5 and B = 90° n ex 3. Solve ABC if b = 4, a = 1. 5 and B = 90° Math 2 Honors - Santowski 4

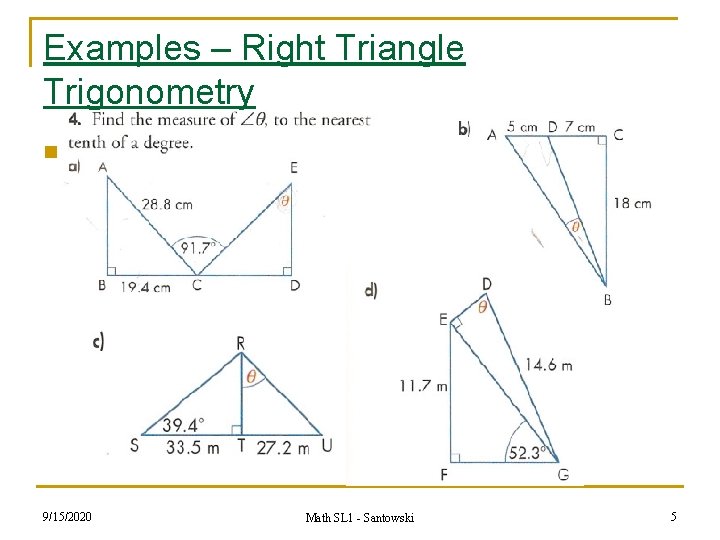
Examples – Right Triangle Trigonometry n 9/15/2020 Math SL 1 - Santowski 5

Examples – Right Triangle Trigonometry n 9/15/2020 Math SL 1 - Santowski 6

(C) Cosine Law B c a C n n n b A The Cosine Law states the following: a² = b² + c² - 2 bccos. A b 2 = a 2 + c 2 - 2 accos. B c 2 = a 2 + b 2 - 2 abcos. C We can use the Cosine Law to work in right and non-right triangles (oblique) in which we know all three sides (SSS) and one in which we know two sides plus the contained angle (SAS). Math 2 Honors - Santowski 7

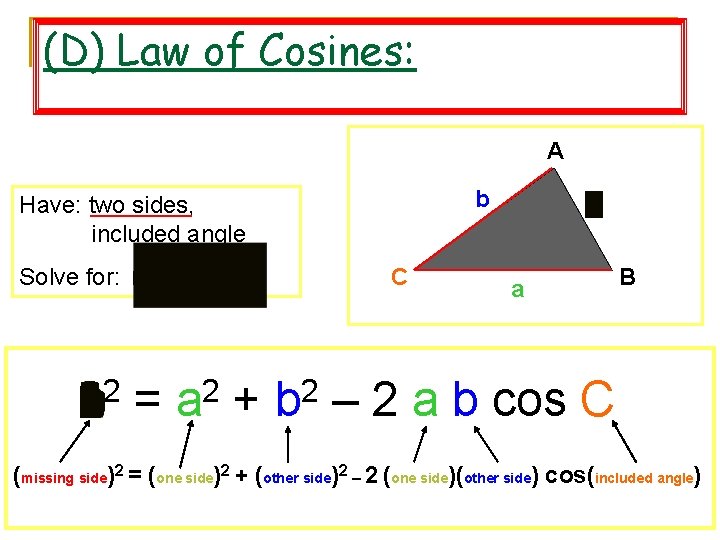
(D) Law of Cosines: A b Have: two sides, included angle Solve for: missing side 2 c = 2 a + C 2 b c a B – 2 a b cos C (missing side)2 = (one side)2 + (other side)2 – 2 (one side)(other side) cos(included angle) Math 2 Honors - Santowski 8

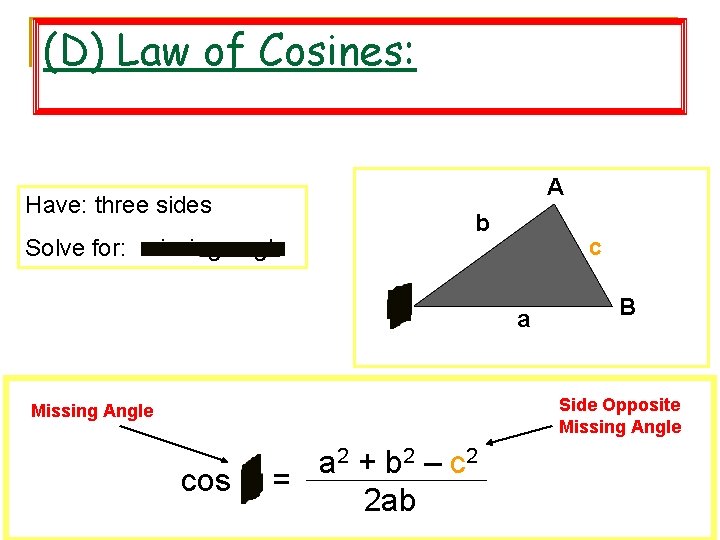
(D) Law of Cosines: A Have: three sides b Solve for: missing angle C c a B Side Opposite Missing Angle a 2 + b 2 – c 2 cos C = 2 ab Math 2 Honors - Santowski 9

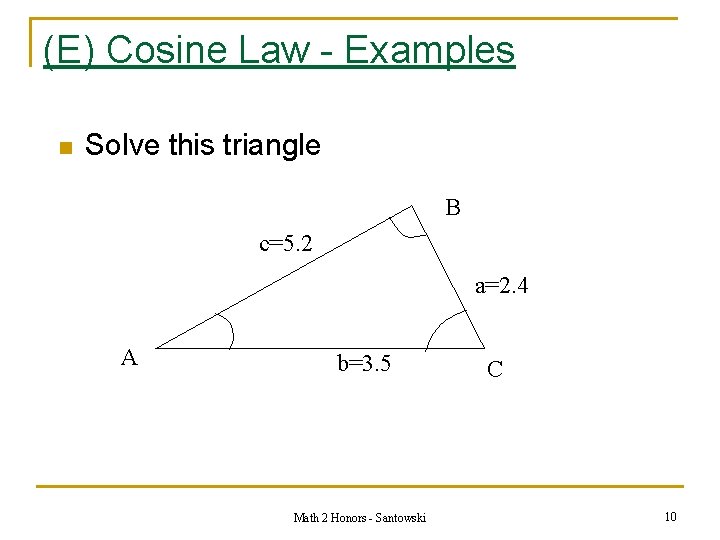
(E) Cosine Law - Examples n Solve this triangle B c=5. 2 a=2. 4 A b=3. 5 Math 2 Honors - Santowski C 10

(F) Examples Cosine Law n We can use these new trigonometric relationships in solving for unknown sides and angles in acute triangles: n ex 1. Find c in CDE if C = 56°, d = 4. 7 and e = 8. 5 n ex 2. Find G in GHJ if h = 5. 9, g = 9. 2 and j = 8. 1 n ex 3. Solve CDE if D = 49°, e = 3. 7 and c = 5. 1 Math 2 Honors - Santowski 11

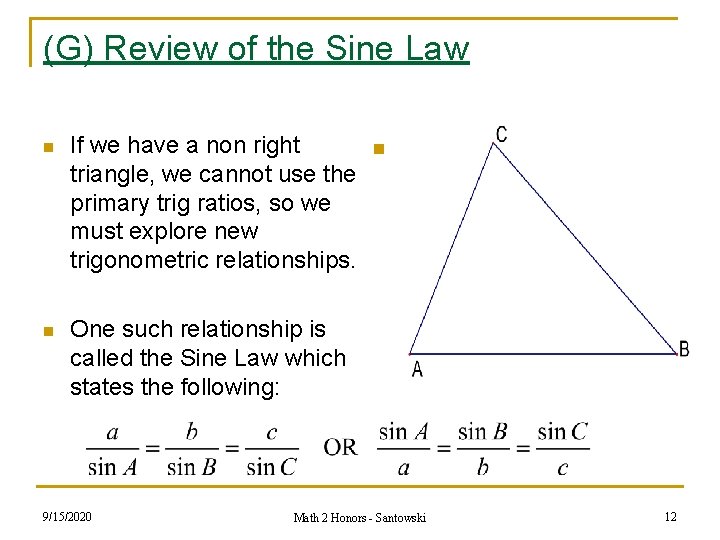
(G) Review of the Sine Law n If we have a non right triangle, we cannot use the primary trig ratios, so we must explore new trigonometric relationships. n One such relationship is called the Sine Law which states the following: 9/15/2020 n Math 2 Honors - Santowski 12

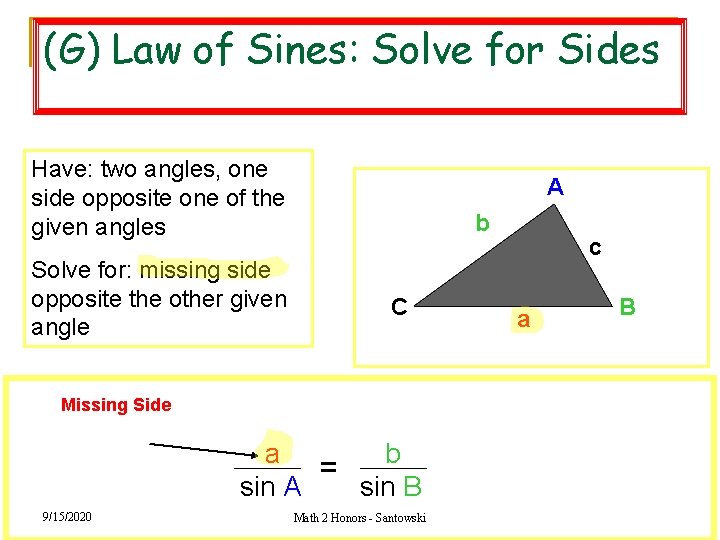
(G) Law of Sines: Solve for Sides Have: two angles, one side opposite one of the given angles Solve for: missing side opposite the other given angle A b C c a B Missing Side a b = sin A sin B 9/15/2020 Math 2 Honors - Santowski 13

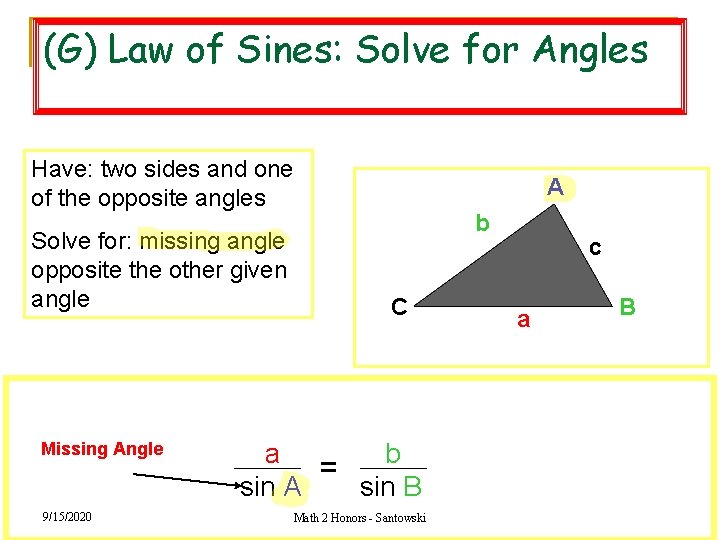
(G) Law of Sines: Solve for Angles Have: two sides and one of the opposite angles Solve for: missing angle opposite the other given angle Missing Angle 9/15/2020 A b C c a B a b = sin A sin B Math 2 Honors - Santowski 14

(H) Examples Sine Law n We can use these new trigonometric relationships in solving for unknown sides and angles in acute triangles: n ex 4. Find A in ABC if a = 10. 4, c = 12. 8 and C = 75° n ex 5. Find a in ABC if A = 84°, B = 36°, and b = 3. 9 n ex 6. Solve EFG if E = 82°, e = 11. 8, and F = 25° n There is one limitation on the Sine Law, in that it can only be applied if a side and its opposite angle is known. If not, the Sine Law cannot be used. 9/15/2020 Math 2 Honors - Santowski 15

(H) Homework n Nelson S 6. 1 Math 2 Honors - Santowski 16