Lesson 4 Reals Examples of real numbers 123

Lesson 4 Reals Ø Examples of real numbers: 123. 456, 5, 2/3, , Ø Reals in daily life height, weight, speed, distance, interest-rate, … Ø Reals include integers. There are infinite reals between any two different reals, e. g. , between 1. 1 and 1. 2 Ø The set of floating-point numbers is a subset of reals. A floating-point number consists of an integer part and a fractional part. E. g. , 12. 125, -0. 625, 0. 0, 33. 0937 1

Ø There are infinite floating-point numbers Ø Only a subset of floating-point numbers is represented in computers. An arbitrary real is approximated by a nearby representable floating point number. E. g. 0. 66666666666 0. 666666667 1/3 0. 33333333 3. 141592653589793 1. 4142135623730951 2

Ø To compute the surface area and volume of a sphere const double PI = 3. 141592653589793; double radius, area, volume; cout << "Enter the radius of a sphere in cm: "; cin >> radius; area = 4. 0 * PI * radius; volume = 4. 0 * PI * radius / 3. 0; cout << "Radius is " << radius << " cmn"; cout << "Surface area is " << area << " cm^2n"; cout << "Volume is " << volume << " cm^3n"; Enter the radius of a sphere in cm: 2. 0 Radius is 2 cm Surface area is 50. 2655 cm^2 Volume is 33. 5103 cm^3 3

Ø A floating-point number can be represented in scientific notation where a value is represented as fraction 10 exponent , where 1 abs( fraction) < 10 (The fraction is called mantissa in some books. ) Fixed Point Notation 120. 0010004 0. 0 12345600000 0. 00005 300000 102 0. 000000 09 200 Scientific Notation 1. 2 102 1. 0004 10 -3 0. 0 100 1. 23456 1010 5. 0 10 -9 3. 0 10102 9. 0 10 -201 4

Ø Consider a decimal computer that uses 4 digits to represent the fraction and 2 digits for the exponent. Scientific Notation In the decimal computer 1. 2 102 +1200+02 -1. 0004 10 -3 -1000 -03 0. 0 100 +0000+00 -1. 23456 1011 -1234+11 5. 0 10 -10 +5000 -10 -3. 0 10102 -INFINITY (Overflow) 9. 0 10 -200 +0000+00 (Underflow) 1. 0 10100 INFINITY (Rounding error) (Overflow) 5

Ø The double values in a computer are represented in scientific notation except that its base is 2 instead of 10. Ø Eight bytes ( 64 bits) are used to represent a double value: 1 bit for the sign of the value, 52 for the fraction and 11 for the exponent (including the sign of the exponent). Ø The total number of representable values is at most Ø The minimum and maximum of double values in a computer are defined as symbolic constants in the library <cfloat>: DBL_MIN, DBL_MAX 6

Ø A very special double “value” is the constant Infinity Ø An overflow occurs if the magnitude of the result of an operation is larger than the maximum. If the result is positive, it is set to +Infinity. A negative one is set to –Infinity. Ø A loss of precision occurs if the magnitude of the result is mildly less than the minimum. Ø An underflow occurs if the result is less than the minimum by a fold of 10 -16. In such case, the result is set to 0. 7

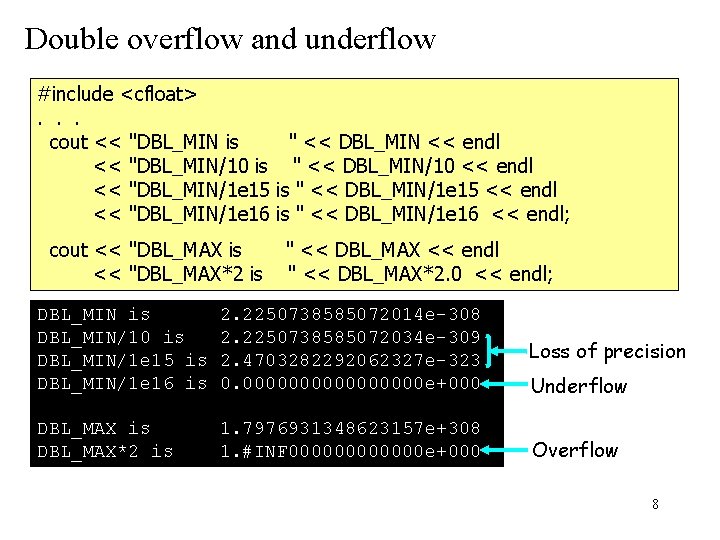
Double overflow and underflow #include <cfloat>. . . cout << "DBL_MIN is " << DBL_MIN << endl << "DBL_MIN/10 is " << DBL_MIN/10 << endl << "DBL_MIN/1 e 15 is " << DBL_MIN/1 e 15 << endl << "DBL_MIN/1 e 16 is " << DBL_MIN/1 e 16 << endl; cout << "DBL_MAX is << "DBL_MAX*2 is " << DBL_MAX << endl " << DBL_MAX*2. 0 << endl; DBL_MIN is DBL_MIN/10 is DBL_MIN/1 e 15 is DBL_MIN/1 e 16 is 2. 2250738585072014 e-308 2. 2250738585072034 e-309 2. 4703282292062327 e-323 0. 00000000 e+000 Loss of precision DBL_MAX is DBL_MAX*2 is 1. 7976931348623157 e+308 1. #INF 000000 e+000 Overflow Underflow 8

Ø Examples of double constants: 123. 456 , 5. , 0. 0 , 0. , . 0 , +9. , . 123456789999999 , 1. 09 e-3 , -1 E 10 , 0. 1 e 5 Ø Examples of invalid double constants: 123, 0, 1 d 3, . e-2, -e 5, 2. 0 e 0. 5 Ø Declaration of double variables double area; double x, y, z; double price = 100. 5; //initial value undefined //price is initialized to 100. 5 9

The syntax rules of double constants Adv ance d <sign> + | | <digit> 0 | 1 | …|9 <digits> <digit> | <digit> <digits> <fixed> <digits>. |. <digits> | <digits> <expn> {e | E} <sign> <digits> | <double const> <sign> <fixed> <expn> | <sign><digits><expn> denotes an empty string (nothing) | denotes “or” 10

Ø double operations Ø Unary operations +x //Identity –x //Negation Ø Binary operations x + y x – y x * y x / y //Addition //Subtraction //Multiplication //Division, y 0 Note that the same symbols are used to denote int and double operators. These operators are ______. Ø The precedence and association rules are the same as that of int. 11

Ø In a pure-mode operation, all the operands are of type double and the result is of type double, eg, 2. 0 * PI Ø In a mixed-mode binary operation, e. g. , 1 + 3. 0 , one operand is of type int and the other is of double. The int value is first cast (converted) to the equivalent double value (automatically) before the double operation is carried out. The answer is of type double. Ø Mixed-mode assignment: <double var> = <int expr>; When an int value is assigned to a double variable, the int value is cast automatically to the equivalent double value before the assignment. E. g. , double d; //declare d as a double variable d = 13; //convert 13 to 13. 0 before the assignment 12

Ø No precision is lost when an int value is cast into a double value. Ø When a double value is assigned to an int variable, the value is cast automatically to an int value equal to the integer portion of the double value. The fraction is lost. A warning is issued for the possible loss of precision. E. g. , int i; i = 13. 999; i = d; //declare i as an int variable //i is equal to 13. A warning is issued //i = floor(d). A warning is issued. #> <program name> <line [Warning] assignment to `int' from `double' 13

Ø (int) is the casting operator that converts a value of other type to an int value. E. g. , (int) 3. 9 equal to the integer value 3 (int) -3. 9 equal to the integer value -3 Note that there is no rounding, the fraction of the operand is merely discarded (truncation). Ø The casting operator has higher priority than all the binary operators. E. g. , (int) 3. 5 / 0. 5 equals (int) (3. 5 / 0. 5) equals 14

Ø Cast a double value to an int value before assigning it to an int variable (highly recommended) <int var> = (int) (<double expr>); E. g. , i = (int) d; i = (int) (d / 13. 3); Ø Similarly, you may convert a value of other type into the equivalent double value using the casting operator (double). What are the results of the following? int i = 7; d = (double) i / 2; d = (double) (i / 2); 15

Let j be an int variable and d be a double. Give the value of j or d for each statement below. Give an X for a statement with syntax errors. Mark a statement with a if it may trigger a warning in compilation. ! j = “ 555”; j = 5 / 2; j = 5 % 2; j = 5. 0; j = (int) 3. 4 / 1. 1; j = (int) (3. 4 / 1. 1); d = 5 / 2; d = (double) 5 / 2; d = (int) (12. 34567 * 100. 0) / 100. ; d = (int) (12. 34567 * 1000. 0 + 0. 5) / 1000. ; 16

Ø The last example shows a standard trick to perform rounding. Ø The following rounds the digit right after the decimal point, (int) (123. 4567 + 0. 5) Ø The following rounds the second digit after the decimal point, (int) (123. 4567 *10. 0 + 0. 5)/10. 0; Ø The following rounds the third digit after the decimal point, (int) (123. 4567 *100. 0 + 0. 5)/100. 0; 17

cmath library Ø This library provides functions for computing many common mathematical functions. E. g. , sin(x), sqrt(x), . . . Ø To look up the description of a function in cmath ØStart from http: //www. cplus. com/ref/ ØClick cmath or math. h ØClick the function you want to look up 18

19

20

21

22

Some useful functions in the library cmath double fabs( double x) //abs(x) is for int values!!! Returns the absolute value of a double value. double cos( double x) //sin( x), tan(x), … Returns the trigonometric cosine of an angle. double atan( double x) //asin(x), acos(x) Returns the arc tangent of an angle, in the range of -pi/2 through pi/2. double floor( double x) //Round down Returns the largest integer that is less than or equal to x. floor of 2. 3 is 2. 0; floor of 3. 8 is 3. 0 floor of -2. 3 is -3. 0; floor of -3. 8 is -4. 0 23

More useful methods in cmath double ceil (double x ) Returns the smallest integer that is greater or equal to x (round up). Eg, ceil of 2. 3 is 3. 0; ceil of 3. 8 is 4. 0 ceil of -2. 3 is -2. 0; ceil of -3. 8 is -3. 0 double sqrt( double x) double exp( double x) double log( double x) double pow( double x, double y) returns the natural log, i. e. , ln( x) returns 24

Assuming that n is of int and x, y are of double, write a C++ statement for the following. Make use of the functions pow( x, y) and sqrt( x) in cmath. 25

Many new versions of math. h contain the definitions of e and const double M_E = 2. 71828459045; The double value that is closest to e, the base of the natural logarithms. const double M_PI = 3. 141592653589793; The double value that is closest to pi, the ratio of the circumference of a circle to its diameter. 26

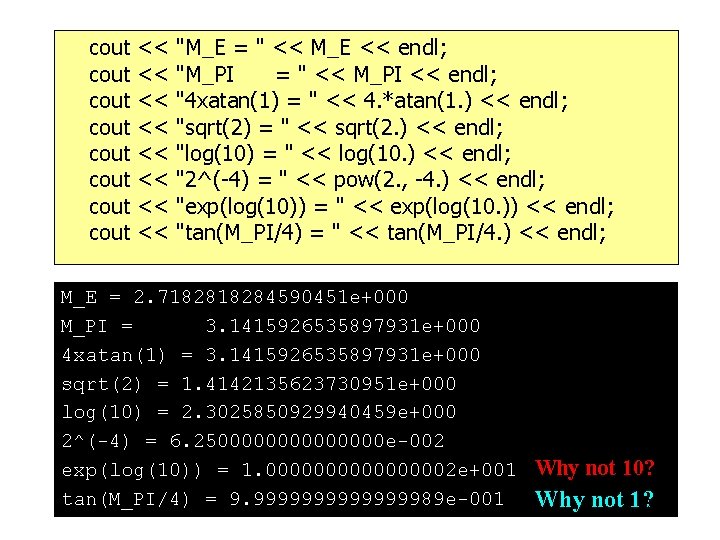
cout cout << << "M_E = " << M_E << endl; "M_PI = " << M_PI << endl; "4 xatan(1) = " << 4. *atan(1. ) << endl; "sqrt(2) = " << sqrt(2. ) << endl; "log(10) = " << log(10. ) << endl; "2^(-4) = " << pow(2. , -4. ) << endl; "exp(log(10)) = " << exp(log(10. )) << endl; "tan(M_PI/4) = " << tan(M_PI/4. ) << endl; M_E = 2. 718284590451 e+000 M_PI = 3. 1415926535897931 e+000 4 xatan(1) = 3. 1415926535897931 e+000 sqrt(2) = 1. 4142135623730951 e+000 log(10) = 2. 3025850929940459 e+000 2^(-4) = 6. 250000000 e-002 exp(log(10)) = 1. 000000002 e+001 Why not 10? tan(M_PI/4) = 9. 999999989 e-001 Why not 1? 27

Ø When double overflow occurs, the result is set to Infinity Adv or –Infinity. a nced Ø The result of 1. 0/0. 0 is undefined in mathematics. It is set to Infinity in C++. Ø The result of 0. 0/0. 0 is undefined in mathematics. It is set to Na. N in C++. Na. N is the acronym of “Not a Number”. Ø A unique feature of Na. N is that it is NOT equal to itself. If a variable is not equal to itself, we can conclude that its value is Na. N. Ø Reference: IEEE Standard 754 on floating point number representation. 28

Ø A program that shows overflow and the checking of Adv ance Infinity and –Infinity. d #include <cmath>. . . double d 1, d 2; d 1 = exp( 1000. ); cout << "exp( 1000. ) is " << d 1; if (d 1 == numeric_limits<double>: : infinity()) cout << " (Infinity)" << endl; d 2 = -1. /0. ; cout << "-1. /0. is " << d 2; if (d 2 == -numeric_limits<double>: : infinity()) cout << " (-Infinity)" << endl; exp( 1000. ) is 1. #INF (Infinity) -1. /0. is -1. #INF (-Infinity) 29

Ø A program that shows results of Na. N in computation and Adv ance the checking of Na. N d d 3 = log( -1. 0); cout << "log( -1. 0) is " << d 3; if (d 3 != d 3) cout << " (Na. N)" << endl; d 4 = sqrt( -1. 0); cout << "sqrt( -1. 0) is " << d 4; if (d 4 != d 4) cout << " (Na. N)" << endl; d 5 = 0. 0 / 0. 0; cout << "0. 0/0. 0 is " << d 5; if (d 5 != d 5) cout << " (Na. N)" << endl; log( -1. 0) is -1. #IND (Na. N) sqrt( -1. 0) is -1. #IND (Na. N) 0. 0/0. 0 is 1. #QNAN (Na. N) 30

Specify a data type (int, double, or string) for each of the constants below. Put down X for any invalid constants. (i) INT_MIN (ii) Tic. Tac. Toe (iii) 4. (iv) INFINITY (v) DBL_MAX (vi) 1 E-. 5 (vii) Na. N (viii) 1. 5 E-3 (ix) “ 12345. 678” 31

Round-off errors The errors that are introduced by the inexactness of the floating point number representations for reals. These errors may be accumulated and magnified during extensive computation. Ø Inexactness example (in a machine holding 4 decimal digits) 1/3 0. 3333 (Error is 0. 0000333…) Ø Accumulation example 1/3 + 1/3 0. 6666 (Error is 0. 0000666…) Ø Magnifying example 1000 * (1/3 – 0. 333) = 1000 * (0. 3333 – 0. 333) = 0. 3 32 (Error is 0. 0333…)

Ø The following shows a substantial error made in a calculator that holds 4 decimal digits. 33

Ø Give an example of syntax errors in a program. Ø Give an example of run-time errors during the execution of a program. Ø Will a computer issue an error message for a logic error in a program. Ø The statement below prints False. Explain. if ( sqrt(2. 0) * sqrt(2. 0) == 2. 0 ) cout << "True"; else cout << "False"; 34

Simple input of double values Ø The operation is similar to the input of an int value. To input a value from the standard input device for the double variable d, write cin >> d; When this statement is executed, the cpu suspends the running of the program until a user keys in a sequence of characters and eventually presses the <Enter> key. The cpu then looks for a string that represents a valid double value in the input sequence. When cpu finds the string, it converts the string into a double value and assigns it to d. Leading blanks and newline characters are skipped. If extra characters are typed, the next input operation starts from the character immediately after the string. 35

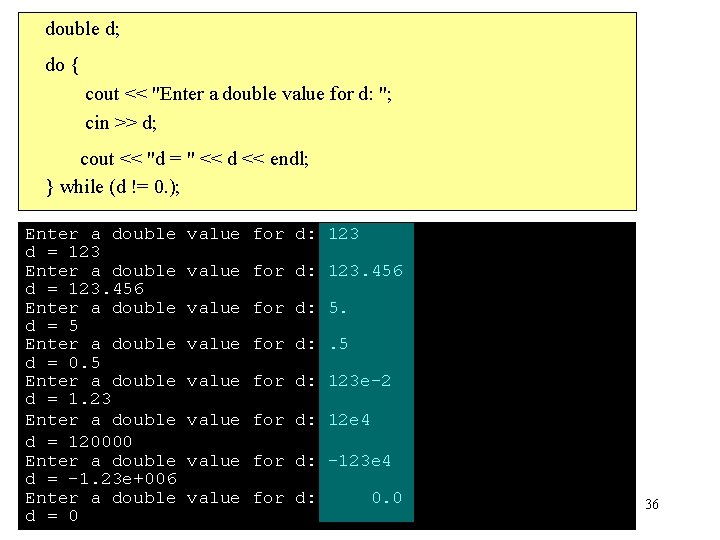
double d; do { cout << "Enter a double value for d: "; cin >> d; cout << "d = " << d << endl; } while (d != 0. ); Enter a double d = 123. 456 Enter a double d = 5 Enter a double d = 0. 5 Enter a double d = 1. 23 Enter a double d = 120000 Enter a double d = -1. 23 e+006 Enter a double d = 0 value for d: 123. 456 value for d: 5. value for d: . 5 value for d: 123 e-2 value for d: 12 e 4 value for d: -123 e 4 value for d: 0. 0 36

Simple output of double values Ø To print a double value in the dialogue window, write cout << <double expr>; The computer will evaluate the expression, then print the result in the dialogue window. Enter a double value d = 123. 456 Enter a double value d = 1. 23 Enter a double value d = 120000 Enter a double value d = -123456 Enter a double value d = -1. 3457 e+006 for d: 123. 456 for d: 123 e-2 for d: 12 e 4 for d: -1234567 37

Enter a double value d = -0. 0001 Enter a double value d = -1 e-005 Enter a double value d = 0. 123457 Enter a double value d = -1. 23457 e+010 for d: -1 e-4 for d: -1 e-5 for d: 0. 123456789 for d: -12345678900 Ø The ordinary form, eg, 123. 456, is called fixed-point notation. The other one is called scientific notation, eg, 1. 23456 e 2. The default width, precision and notation used are machine dependent. (In our system, the default format, fixed-point or scientific, is determined by the magnitude of an output value. ) 38

Ø To specify an output notation for double values, write cout. setf(ios: : fixed); or cout. setf(ios: : scientific); Ø To specify the number of significant digits in the output values, write cout. precision( <int value> ); 39

Ø To insist showing the decimal point and the trailing zero’s, write cout. setf(ios: : showpoint); cout. setf(ios: : scientific); cout. precision(16); cout. setf(ios: : showpoint); Enter a double value for d: 1234 d = 1. 2340000000 e+003 Enter a double value for d: 0. 12345678 d = 1. 234567800000 e-001 Enter a double value for d: -1234. 5678 d = -1. 234567800000 e+003 Enter a double value for d: 1234 e 100 d = 1. 2340000000 e+103 Enter a double value for d: 1234567890123456789 d = 1. 2345678901234568 e+018 Enter a double value for d: -0. 000001234567890123456789 d = -1. 2345678901234568 e-011 Enter a double value for d: 0 e 0 d = 0. 00000000 e+000 40

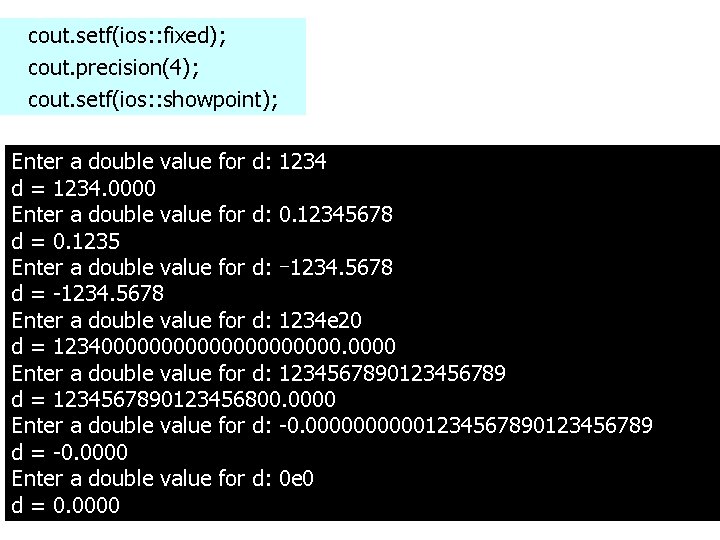
cout. setf(ios: : fixed); cout. precision(4); cout. setf(ios: : showpoint); Enter a double value for d: 1234 d = 1234. 0000 Enter a double value for d: 0. 12345678 d = 0. 1235 Enter a double value for d: -1234. 5678 d = -1234. 5678 Enter a double value for d: 1234 e 20 d = 12340000000000 Enter a double value for d: 1234567890123456789 d = 1234567890123456800. 0000 Enter a double value for d: -0. 000001234567890123456789 d = -0. 0000 Enter a double value for d: 0 e 0 41 d = 0. 0000

Ø Another data type for representing reals in C++ is float. Ø A float value occupies 32 bits (4 bytes). These values are described as single precision in some books. Ø float data are more storage efficient and probably faster in computation. But the results are far less accurate due to round-off errors. 42

Reading Assignment Ø Chapter 2, p. 60 – 72, 93 -108 Ø Chapter 5, P. 247 -252 43