Lesson 4 8 Core Focus on Linear Equations

Lesson 4. 8 Core Focus on Linear Equations Systems of Linear Inequalities

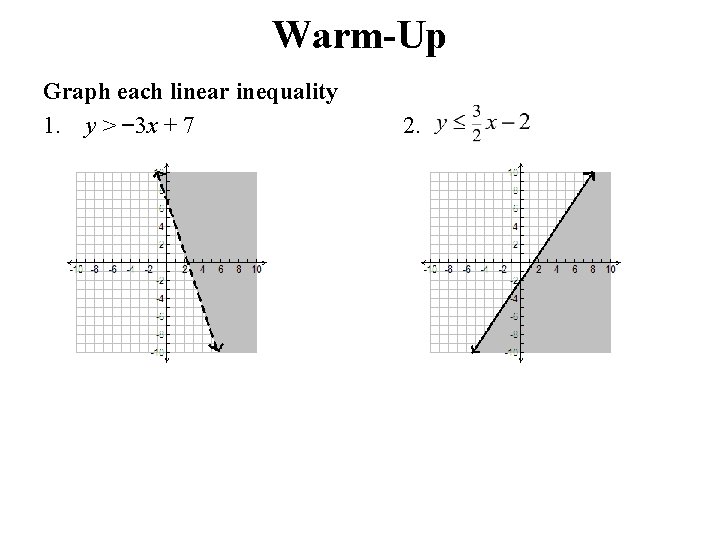
Warm-Up Graph each linear inequality 1. y > − 3 x + 7 2.

Lesson 4. 8 Systems of Linear Inequalities Solve a system of linear inequalities by graphing.

Example 1 Graph the solution to the system of linear inequalities: Graph the boundary line by graphing Use a solid line to connect the points since the inequality symbol is ≤. . Choose (3, 6) as a test point. Substitute the coordinates into the original inequality to see if the statement is true or false. Six is NOT less than or equal to – 1 so the statement is false. Shade the entire side (below the boundary line) that does not contain the test point (3, 6).

Example 1 Continued… Graph the solution to the system of linear inequalities: Graph the boundary line of the second inequality by graphing. Use a solid line to connect the points since the inequality symbol is ≥. Choose (3, 6) as a test point. Substitute the coordinates into the original inequality to see if the statement is true or false. Six is greater than – 5 so the statement is true. Shade the entire side that contains the test point (3, 6).

Example 1 Continued… Graph the solution to the system of linear inequalities: The solution to the system of inequalities is where the shaded regions overlap. The ordered pairs in this region make true statements in both inequalities.

Graphing Systems of Linear Inequalities in Two-Variables 1. Graph each linear inequality in the system on a single coordinate plane. 2. The solution to the system of inequalities is where the shaded regions overlap.

Example 2 Is the point (− 4, − 2) a solution to the system of inequalities formed by y > x + 1 and y < 2 x + 6? Test the point (– 4, – 2) in y > x + 1. y > x+1 – 2 > – 4 + 1 – 2 > – 3 TRUE Test the point (– 4, – 2) in y < 2 x + 6 – 2 < 2(– 4) + 6 – 2 < – 2 FALSE Since the point does not make both equations true, it is NOT a solution to the system of inequalities.

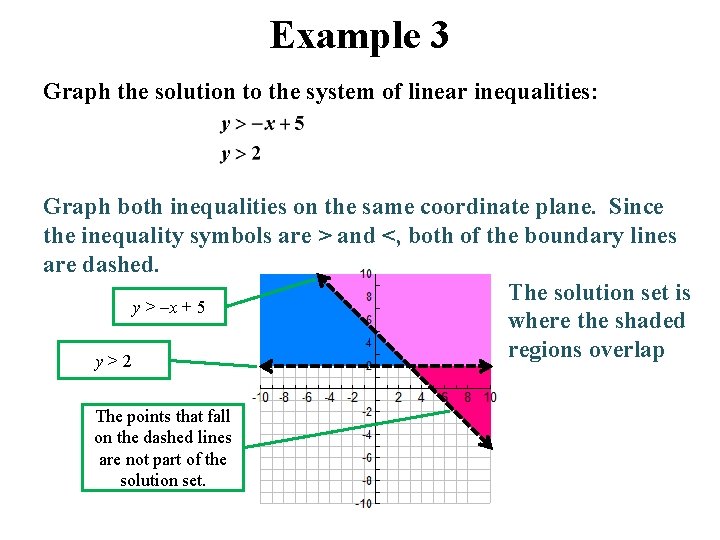
Example 3 Graph the solution to the system of linear inequalities: Graph both inequalities on the same coordinate plane. Since the inequality symbols are > and <, both of the boundary lines are dashed. The solution set is y > –x + 5 where the shaded regions overlap y>2 The points that fall on the dashed lines are not part of the solution set.

Communication Prompt Describe the similarities and differences between the solution to a system of linear equations and a system of linear inequalities.

Exit Problems Graph the solution to the system of inequalities: y < − 2 x + 4