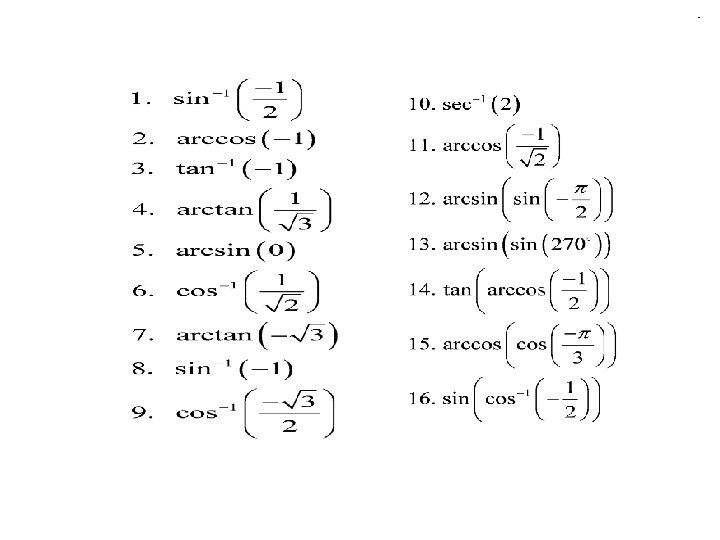Lesson 4 7 Inverse Trigonometric Functions Previously you




![Using the domain restricted to [-π/2 ; π/2] let’s graph y = arcsin x Using the domain restricted to [-π/2 ; π/2] let’s graph y = arcsin x](https://slidetodoc.com/presentation_image_h/91dd71fff2a6f89328adc0836c4d3b3e/image-9.jpg)







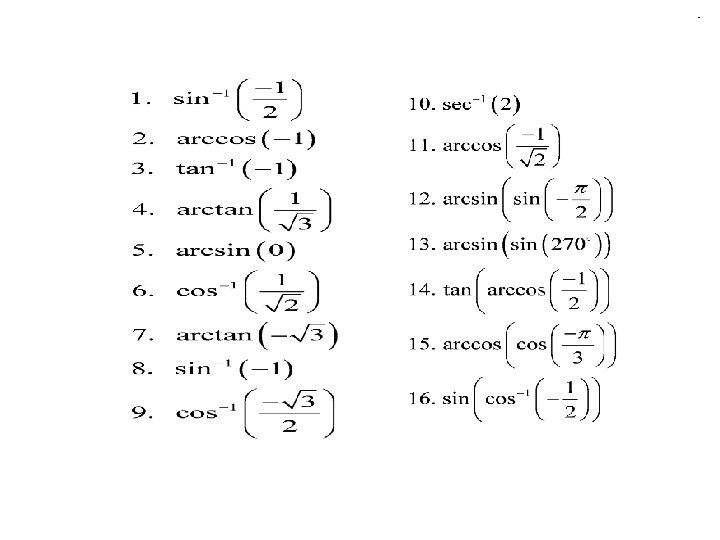

- Slides: 24

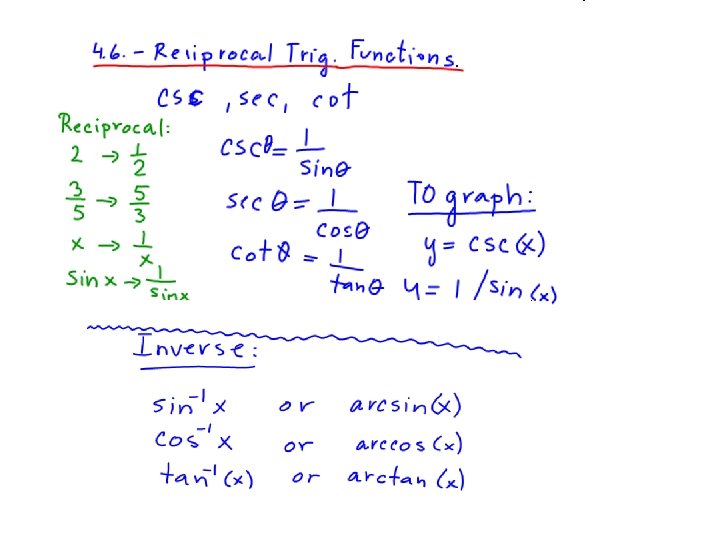
Lesson 4. 7. Inverse Trigonometric Functions. Previously you have learned To find an inverse of a function, let every x be y and every y be x, then solve the equation for y. Inverse function notation f¯¹(x) For a function to have an inverse it has to be one-to -one. One x for one y value, and one y for one x value. It will pass the vertical and the horizontal line test. Two inverse functions on the graph reflect over y=x f(x) f¯¹(x) (x, y) (y, x)



Sometimes you just don’t have a nice or convenient algebraic process that will give you an inverse function. Many functions need a special, new rule for their inverse. Some examples of these functions are:

FINDING INVERSE OF A TRIG FUNCTION : Given f(x) = sin (x) y = sin (x) x = sin (y) y = arcsin (x) f¯¹(x) = sin¯¹(x) Inverse Trigonometric function notation: Inverse sine Inverse cosine Inverse tangent change f(x) for y switch x’s and y’s solve for y write using function notation

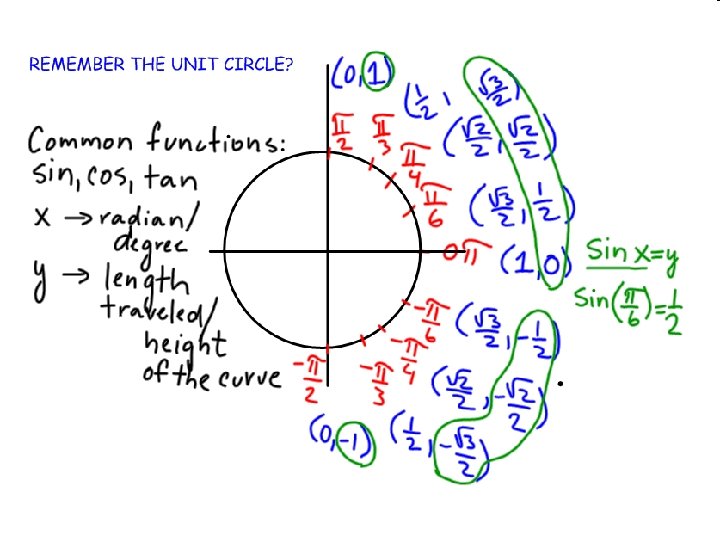
FINDING INVERSE OF A TRIG FUNCTION ALGEBRAICALLY : Given y = sin (x) - ½ = sin ( -π/6) sin (-π/6) = - ½ (-π/6) = sin (- ½ ) switch x and y values (-π/6) = arcsin ( - ½ ) solve for y (-π/6) = sin¯¹( - ½ ) = (-π/6) How does this look on the graph ? ?

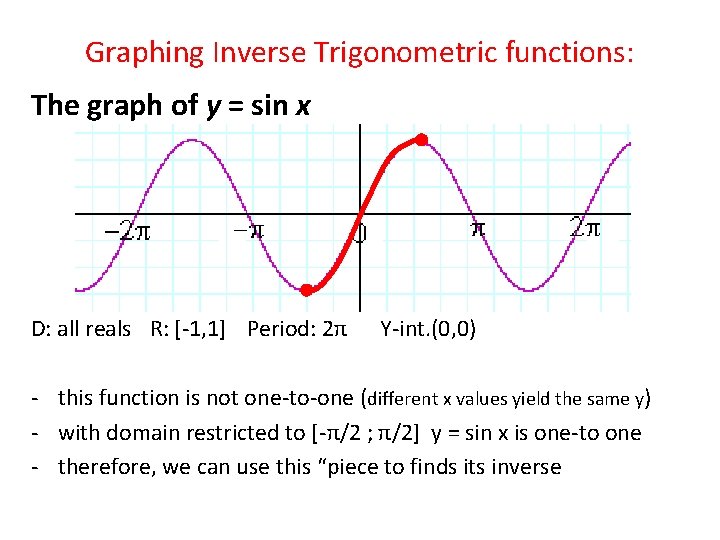
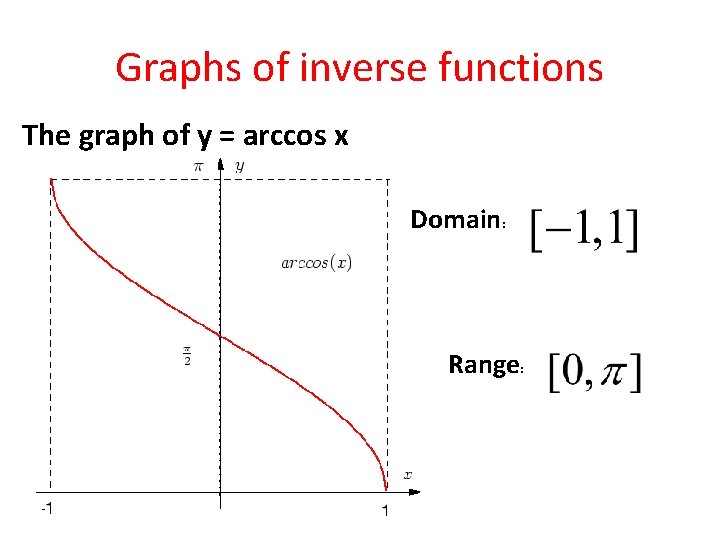
Graphing Inverse Trigonometric functions: The graph of y = sin x D: all reals R: [-1, 1] Period: 2π Y-int. (0, 0) - this function is not one-to-one (different x values yield the same y) - with domain restricted to [-π/2 ; π/2] y = sin x is one-to one - therefore, we can use this “piece to finds its inverse

![Using the domain restricted to π2 π2 lets graph y arcsin x Using the domain restricted to [-π/2 ; π/2] let’s graph y = arcsin x](https://slidetodoc.com/presentation_image_h/91dd71fff2a6f89328adc0836c4d3b3e/image-9.jpg)
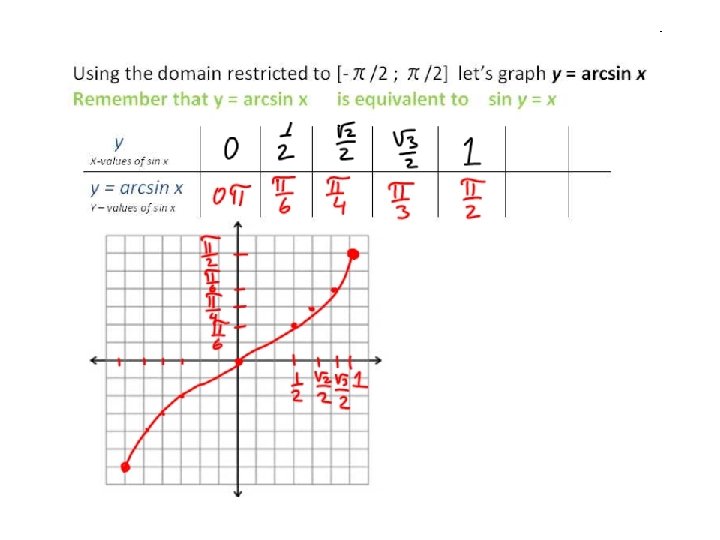
Using the domain restricted to [-π/2 ; π/2] let’s graph y = arcsin x Remember that y = arcsin x is equivalent to sin y = x X y-values of sin x y = arcsin x x – values of sin x


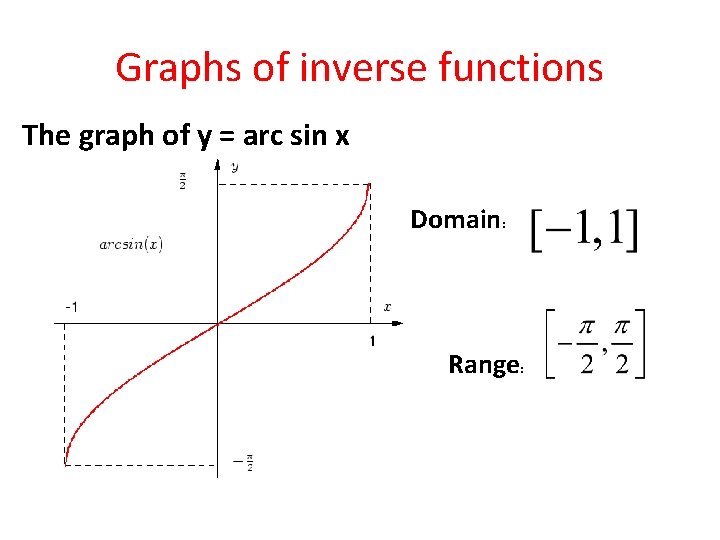
Graphs of inverse functions The graph of y = arc sin x Domain: Range:

NEXT ON THE LIST • ARCCOSINE • Sketch the common curve of y = cos x • Select interval of the cosine that will be one-to -one • Sketch the graph of arccosine

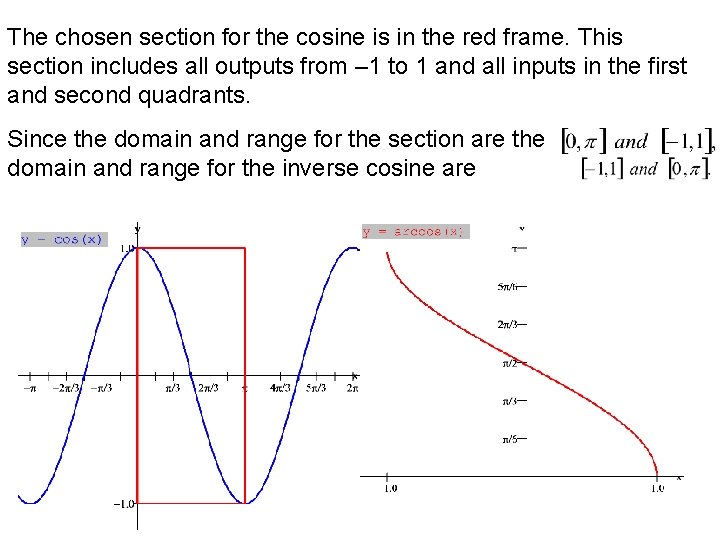
The chosen section for the cosine is in the red frame. This section includes all outputs from – 1 to 1 and all inputs in the first and second quadrants. Since the domain and range for the section are the domain and range for the inverse cosine are

Graphs of inverse functions The graph of y = arccos x Domain: Range:

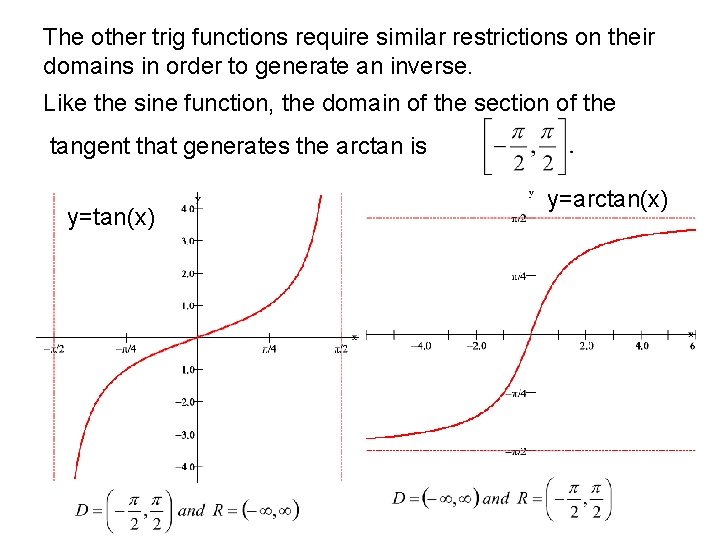
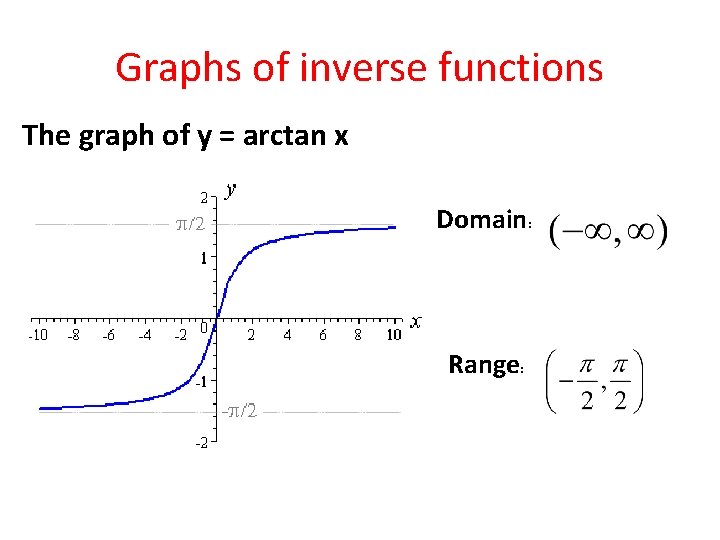
The other trig functions require similar restrictions on their domains in order to generate an inverse. Like the sine function, the domain of the section of the tangent that generates the arctan is y=tan(x) y=arctan(x)

Graphs of inverse functions The graph of y = arctan x Domain: Range:

The table below will summarize the parameters we have so far. Remember, the angle is the input for a trig function and the ratio is the output. For the inverse trig functions the ratio is the input and the angle is the output. arcsin(x) arccos(x) arctan(x) Domain Range When x<0, y=arcsin(x) will be in which quadrant? y<0 in IV When x<0, y=arccos(x) will be in which quadrant? y>0 in II y<0 in IV When x<0, y=arctan(x) will be in which quadrant?

Evaluating Inverse Trigonometric Functions algebraically. When evaluating inverse trigonometric functions, you are “looking for the angle whose (insert: sin, cos, or tan) is x. ” Also, keep in mind the domain and range of each function. Find the exact value for Solution: For what value of x is sin (x) = Sin ( π/3) = therefore ?

Evaluating Inverse Trigonometric Functions algebraically. Find the exact value for Solution: For what value of x is cos (x) = Cos ( 3π/4) = ; therefore ?