Lesson 4 4 Scatter Plots Line of Best

Lesson 4. 4 Scatter Plots & Line of Best Fit Review: 4. 1 - Writing Equations in Slope-Intercept Form 4. 2 - Writing Equations in Point-Slope Form 4. 3 - Writing Equations of Parallel & Perpendicular lines

Objective Interpreting scatter plots, identifying correlations and use of lines of fit to model data EQ #1 – What is a scatter plot & how do you interpret it? Scatter Plots - graph that shows a relationship between two data sets What type of graph is this? Scatter Plot What is the description of the domain? Sugar grams in a smoothie What is the description of the range? Calories in a smoothie based on the number of sugar grams

EQ #1 - continued How many calories are in a smoothie with 56 grams of sugar? 270 calories How many calories are in a smoothie with 70 grams of sugar? 320 calories What “tends” to happen to the number of calories as the grams of sugar increase in a smoothie? As the grams of sugar increases the number of calories also “tends” to increase.
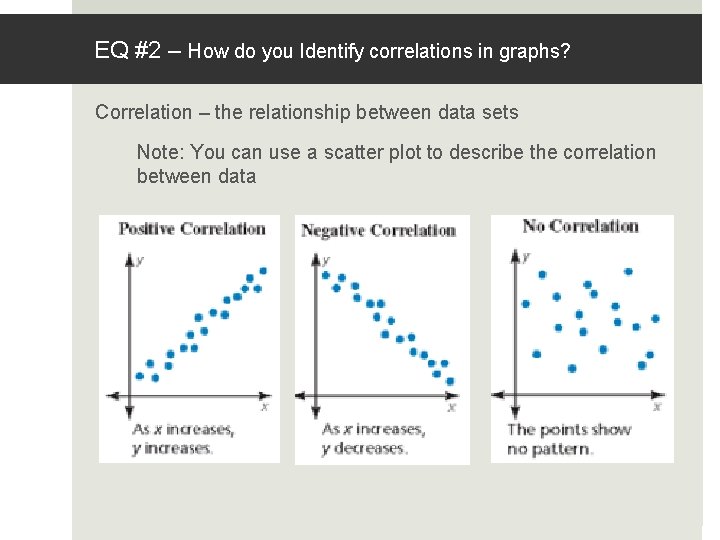
EQ #2 – How do you Identify correlations in graphs? Correlation – the relationship between data sets Note: You can use a scatter plot to describe the correlation between data
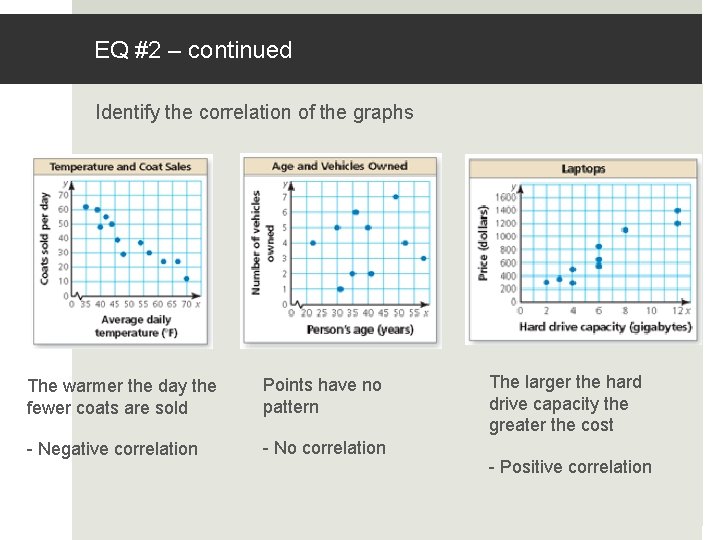
EQ #2 – continued Identify the correlation of the graphs The warmer the day the fewer coats are sold Points have no pattern - Negative correlation - No correlation The larger the hard drive capacity the greater the cost - Positive correlation
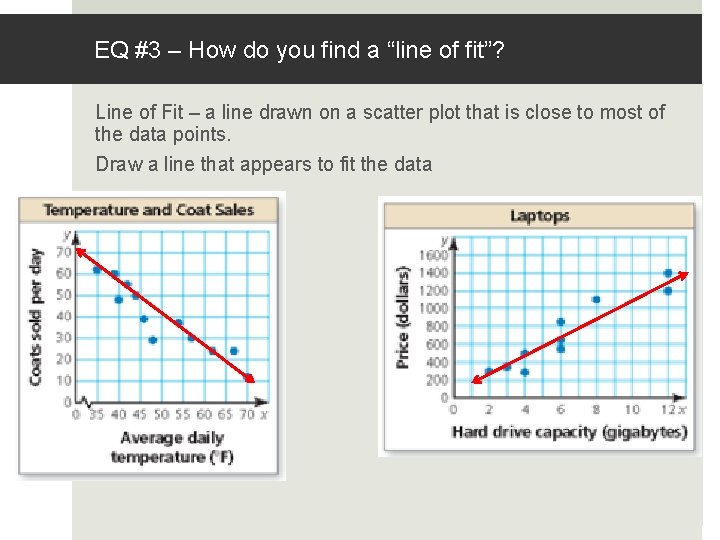
EQ #3 – How do you find a “line of fit”? Line of Fit – a line drawn on a scatter plot that is close to most of the data points. Draw a line that appears to fit the data
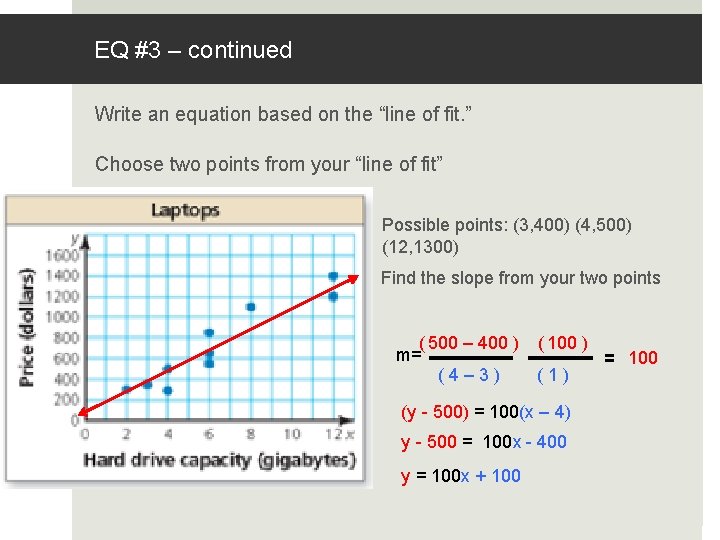
EQ #3 – continued Write an equation based on the “line of fit. ” Choose two points from your “line of fit” Possible points: (3, 400) (4, 500) (12, 1300) Find the slope from your two points ( 500 – 400 ) ( 100 ) m= = 100 (1) (4– 3) (y - 500) = 100(x – 4) y - 500 = 100 x - 400 y = 100 x + 100
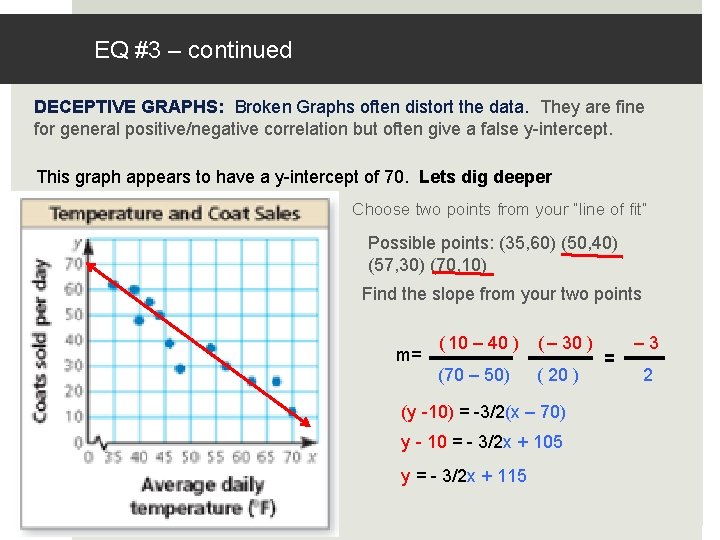
EQ #3 – continued DECEPTIVE GRAPHS: Broken Graphs often distort the data. They are fine for general positive/negative correlation but often give a false y-intercept. This graph appears to have a y-intercept of 70. Lets dig deeper Choose two points from your “line of fit” Possible points: (35, 60) (50, 40) (57, 30) (70, 10) Find the slope from your two points m= ( 10 – 40 ) ( – 30 ) (70 – 50) ( 20 ) (y -10) = -3/2(x – 70) y - 10 = - 3/2 x + 105 y = - 3/2 x + 115 = – 3 2
- Slides: 8