Lesson 4 3 and 4 4 Proving Triangles

Lesson 4. 3 and 4. 4 Proving Triangles are Congruent p. 212

Learning Target I can list the conditions (SAS, SSS) to prove triangles are congruent. n I can identify and use reflexive, symmetric and transitive property in my proof. n

How To Find if Triangles are Congruent Two triangles are congruent if they have: n exactly the same three sides and n exactly the same three angles. n But we don't have to know all three sides and all three angles. . . usually three out of the six is enough. n There are five ways to find if two triangles are congruent: SSS, SAS, ASA, AAS and HL. n

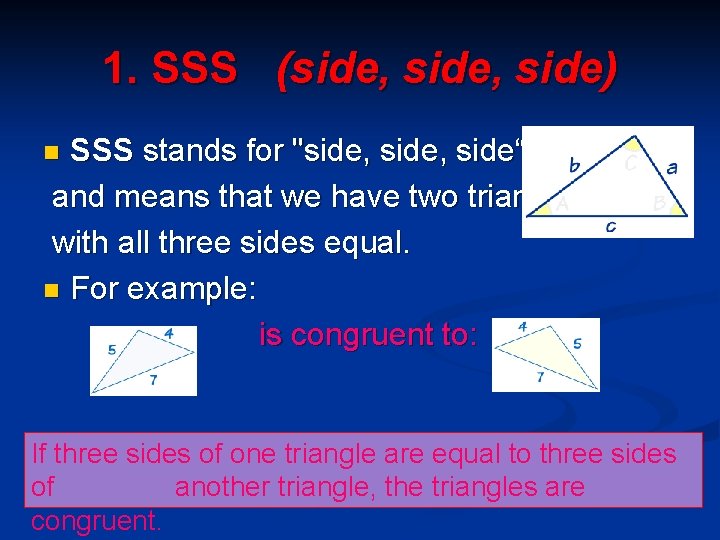
1. SSS (side, side) SSS stands for "side, side“ and means that we have two triangles with all three sides equal. n For example: is congruent to: n If three sides of one triangle are equal to three sides of another triangle, the triangles are congruent.

2. SAS (side, angle, side) SAS stands for "side, angle, side" and means that we have two triangles where we know two sides and the included angle are equal. n For example: is congruent to: n If two sides and the included angle of one triangle are equal to the corresponding sides and angle of another triangle, the triangles are congruent.

3. ASA (angle, side, angle) ASA stands for "angle, side, angle“ and means that we have two triangles where we know two angles and the included side are equal. n For example: is congruent to: n If two angles and the included side of one triangle are equal to the corresponding angles and side of another triangle, the triangles are congruent.

4. AAS (angle, side) n AAS stands for "angle, side“ and means that we have two triangles where we know two angles and the non-included side are equal. n For example: is congruent to: If two angles and the non-included side of one triangle are equal to the corresponding angles and side of another triangle, the triangles are congruent.

5. HL (hypotenuse, leg) n HL stands for "Hypotenuse, Leg" (the longest side of the triangle is called the "hypotenuse", the other two sides are called "legs") and HL applies only to right angledtriangles!

5. HL (hypotenuse, leg) n It means we have two right-angled triangles with the same length of hypotenuse and n the same length for one of the other two legs. n It doesn't matter which leg since the triangles could be rotated. n For example: is congruent to n If the hypotenuse and one leg of one right-angled triangle are equal to the corresponding hypotenuse and leg of another right-angled triangle, the two

Caution ! Don't Use "AAA" ! AAA means we are given all three angles of a triangle, but no sides. n This is not enough information to decide if two triangles are congruent! n Because the triangles can have the same angles but be different sizes: n For example: is congruent to n Without knowing at least one side, we can't be sure if two triangles are congruent. .

Proving Triangles are Congruent You have learned to prove that two triangles are congruent by the definition of congruence – that is, by showing that all pairs of corresponding angles and corresponding sides are congruent. THEOREM B Theorem 4. 4 Properties of Congruent Triangles A Reflexive Property of Congruent Triangles Every triangle is congruent to itself. Symmetric Property of Congruent Triangles D If ABC DEF , then . DEF ABC Transitive Property of Congruent Triangles If ABC DEF and , ABC then JKL J DEF JKL C E F L . K Goal 2

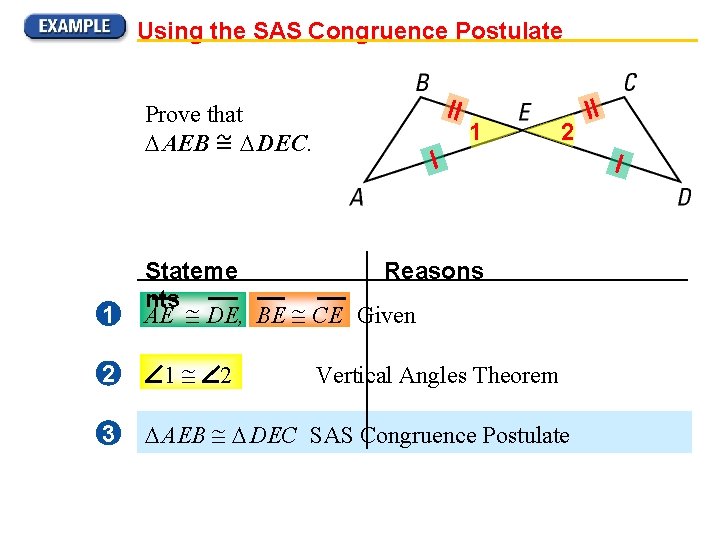
Using the SAS Congruence Postulate Prove that AEB DEC. 1 2 3 1 2 Stateme Reasons nts AE DE, BE CE Given 1 2 Vertical Angles Theorem AEB DEC SAS Congruence Postulate

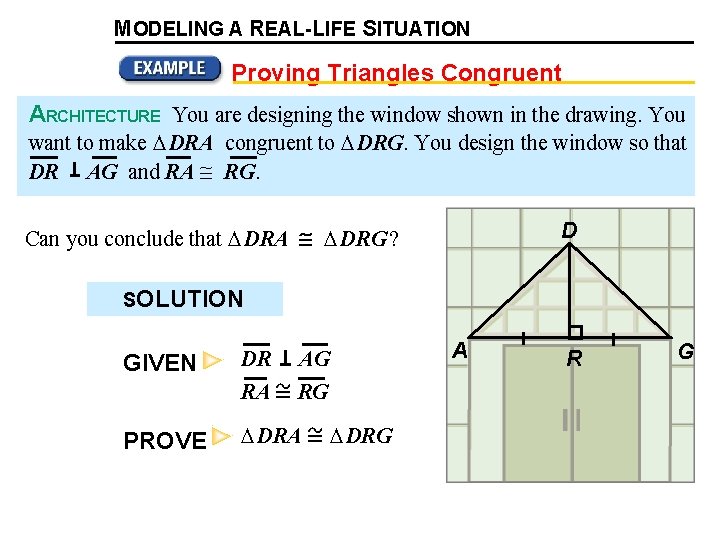
MODELING A REAL-LIFE SITUATION Proving Triangles Congruent ARCHITECTURE You are designing the window shown in the drawing. You want to make DRA congruent to DRG. You design the window so that DR AG and RA RG. D Can you conclude that DRA DRG ? SOLUTION GIVEN DR RA PROVE DRA A AG RG DRG R G

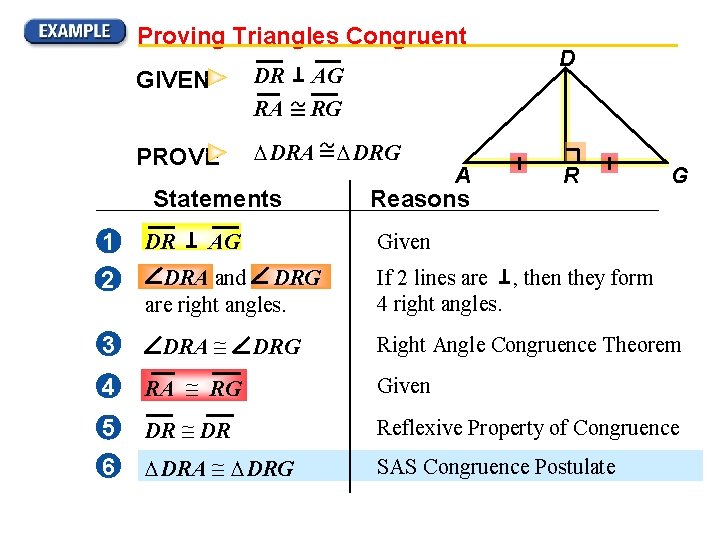
Proving Triangles Congruent GIVEN DR RA AG RG PROVE DRA Statements 1 DR 2 DRA and DRG are right angles. DRG A Reasons D R G Given AG If 2 lines are , then they form 4 right angles. 3 DRA 4 RA RG Given 5 DR Reflexive Property of Congruence 6 DRA DRG SAS Congruence Postulate DRG Right Angle Congruence Theorem

S Given: SP QR; QP PR Prove SPQ SPR Statements 1. SP QR; QP PR 2. QPS and RPS are right ’s. Q Reasons 1. Given P 2. Def. of 3. QPS PRS 3. Rt. Thm. 4. SP 4. Reflexive POC 5. SPQ SPR 5. SAS Post. R

Pair-share Work on classwork on “Congruence Triangle” n Sage and Scribe on #21 to #24 n