Lesson 4 1 Scatter Diagrams and Correlation Objectives

Lesson 4 - 1 Scatter Diagrams and Correlation

Objectives • Draw and interpret scatter diagrams • Understand the properties of the linear correlation coefficient • Compute and interpret the linear correlation coefficient

Vocabulary • Response Variable – variable whose value can be explained by the value of the explanatory or predictor variable • Predictor Variable – independent variable; explains the response variable variability • Lurking Variable – variable that may affect the response variable, but is excluded from the analysis • Positively Associated – if predictor variable goes up, then the response variable goes up (or vice versa) • Negatively Associated – if predictor variable goes up, then the response variable goes down (or vice versa)

Scatter Diagram • Shows relationship between two quantitative variables measured on the same individual. • Each individual in the data set is represented by a point in the scatter diagram. • Explanatory variable plotted on horizontal axis and the response variable plotted on vertical axis. • Do not connect the points when drawing a scatter diagram.

TI-83 Instructions for Scatter Plots • • • Enter explanatory variable in L 1 Enter response variable in L 2 Press 2 nd y= for Stat. Plot, select 1: Plot 1 Turn plot 1 on by highlighting ON and enter Highlight the scatter plot icon and enter Press ZOOM and select 9: Zoom. Stat

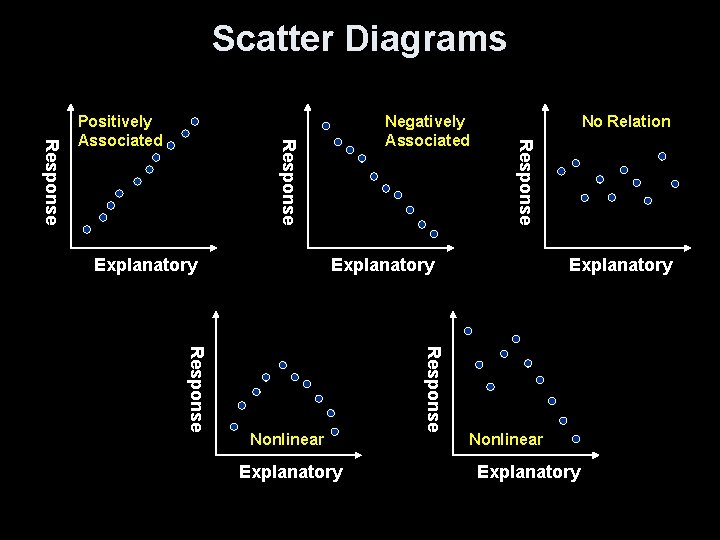
Scatter Diagrams Explanatory No Relation Response Negatively Associated Response Positively Associated Explanatory Response Nonlinear Explanatory

Linear Correlation Coefficient, r Σ r= (xi – x) -----sx Where x is the sample mean of the explanatory variable sx is the sample standard deviation for x y is the sample mean of the response variable sy is the sample standard deviation for y n is the number of individuals in the sample (yi – y) -----sy n– 1 Equivalent Formula for r x Σy Σ Σ x y – -----i i n sxy r= √ = Σ Σ xi 2 ( 2 xi – ----) n Σ yi 2 ( Σ – ----) n √sxx √syy

Properties of the Linear Correlation Coefficient • The linear correlation coefficient is always between -1 and 1 • If r = 1, then the variables have a perfect positive linear relation • If r = -1, then the variables have a perfect negative linear relation • The closer r is to 1, then the stronger the evidence for a positive linear relation • The closer r is to -1, then the stronger the evidence for a negative linear relation • If r is close to zero, then there is little evidence of a linear relation between the two variables. R close to zero does not mean that there is no relation between the two variables • The linear correlation coefficient is a unitless measure of association

TI-83 Instructions for Correlation Coefficient • With explanatory variable in L 1 and response variable in L 2 • Turn diagnostics on by – Go to catalog (2 nd 0) – Scroll down and when diagnostic. On is highlighted, hit enter twice • Press STAT, highlight CALC and select 4: Lin. Reg (ax + b) and hit enter twice • Read r value (last line)

Example 1 2 3 4 5 6 7 8 9 x 3 2 2 4 5 15 22 13 6 5 4 1 y 0 1 2 9 3 1 0 16 5 3 10 11 12 • Draw a scatter plot of the above data y x • Compute the correlation coefficient r = 0. 9613

Observational Data • If bivariate (two variable) data are observational, then we cannot conclude that any relation between the explanatory and response variable are due to cause and effect • Observational versus Experimental Data

Summary and Homework • Summary – Correlation between two variables can be described with both visual and numeric methods – Visual methods • Scatter diagrams • Analogous to histograms for single variables – Numeric methods • Linear correlation coefficient • Analogous to mean and variance for single variables – Care should be taken in the interpretation of linear correlation (nonlinearity and causation) • Homework – pg 203 – 211; 4, 5, 11 -16, 27, 38, 42

Homework Answers • 12: Linear, negative • 14: nonlinear (power function perhaps) • 16 a) IV b) III c) I d) II • 38: Example problem • 42: No linear relationship, but no releationship. Power function relationship (negative parabola)