Lesson 35 Solving quadratic equations Quadratic function Standard

Quadratic function • Standard form of a quadratic function: f(x) = ax 2 +

Finding the zeros of quadratic functions • • • f(x) = 4 x 2

Find the zeros • f(x) = 9 x 2 -64 • f(x) = 2

Roots of an equation • The roots of an equation are the solutions to

Solving quadratic equations • Find the roots of the quadratic equation: • x 2

Zeros of a quadratic function • The graph of a quadratic function shows how

Double root • When a quadratic function has exactly one real zero, that zero

Comparing roots, zeros, and xintercepts • Find the roots, graph the related function and

practice • 3 x 2+6 x=0 • x 2=-3 x+28 • 4 x 2

Writing a quadratic function, given its zeros • Write a quadratic function that has

practice • Write an quadratic function that has zeros -3/2 and 4

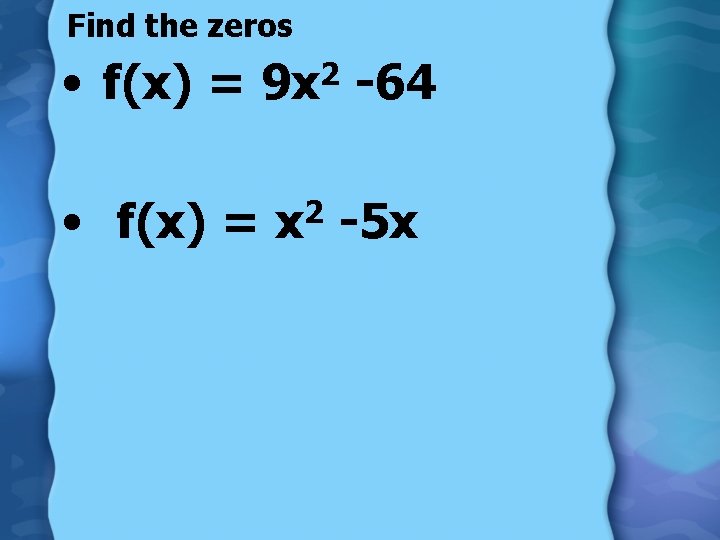
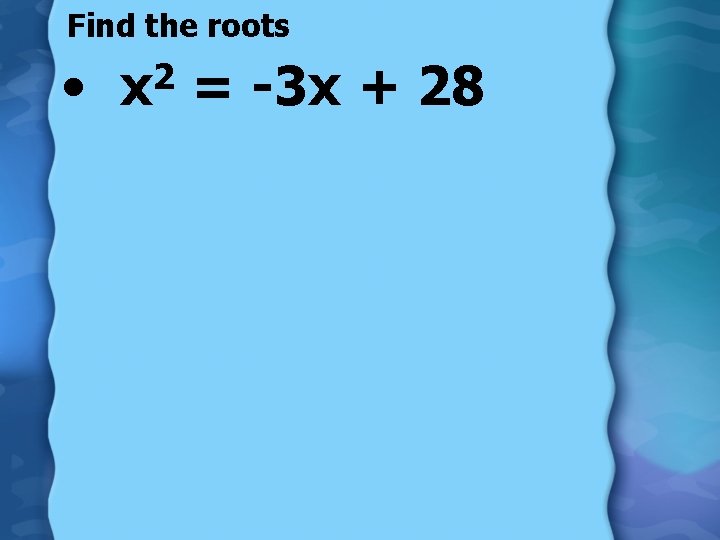
Slides: 13

Download presentation

Lesson 35 Solving quadratic equations

Quadratic function • Standard form of a quadratic function: f(x) = ax 2 + bx + c • To find the zeros of the function, solve the equation for f(x) =0 • So ax 2 + bx + c = 0 • Many can be solved by factoring, and the zero product property • Zero product property • let a and b be real numbers • If ab= 0, then a=0 or b= 0

Finding the zeros of quadratic functions • • • f(x) = 4 x 2 -25 0= 4 x 2 -25 0= (2 x-5)(2 x+5) 2 x-5 = 0 or 2 x+5 = 0 2 x=5 2 x = -5 x = 5/2 or x = -5/2 • • • f(x) = 2 x 2 + x 0 = 2 x 2 +x 0 = x(2 x+1) 0=x or 2 x+1 =0 2 x = -1/2

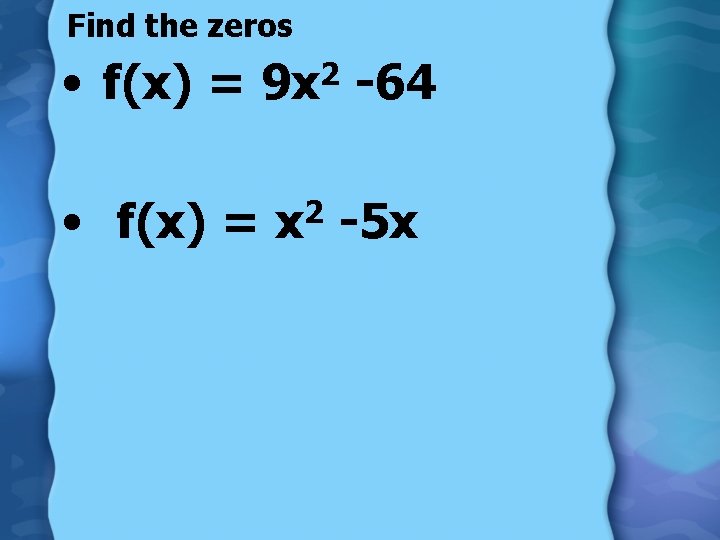
Find the zeros • f(x) = 9 x 2 -64 • f(x) = 2 x -5 x

Roots of an equation • The roots of an equation are the solutions to the equation

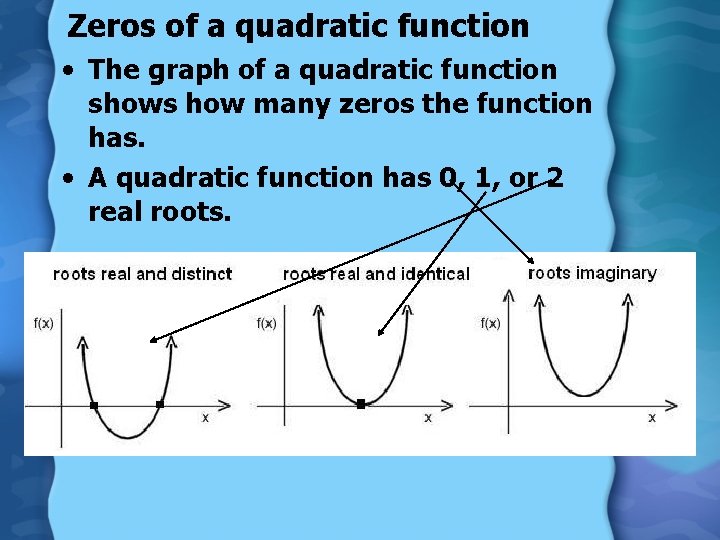
Solving quadratic equations • Find the roots of the quadratic equation: • x 2 = -2 x + 15 • x 2 + 2 x -15 =0 • (x+5)(x-3) = 0 • x+5 = 0 or x-3 = 0 • x = -5 or x = 3 • The graph of a quadratic function shows how many zeros the function has.

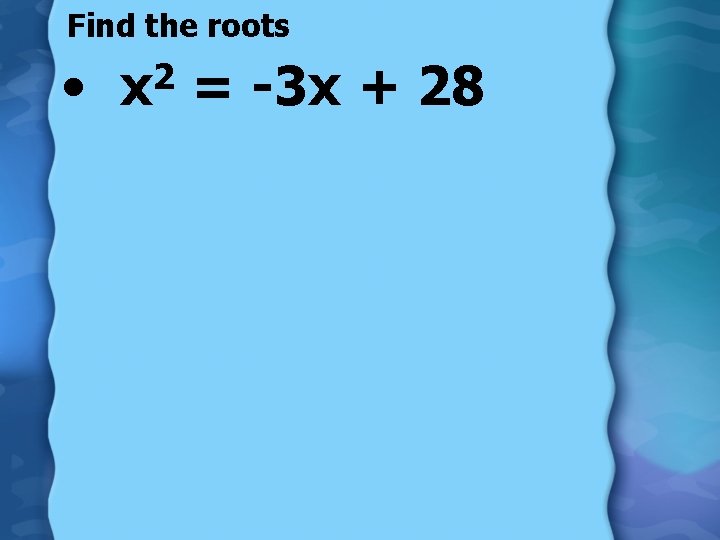
Find the roots • 2 x = -3 x + 28

Zeros of a quadratic function • The graph of a quadratic function shows how many zeros the function has. • A quadratic function has 0, 1, or 2 real roots.

Double root • When a quadratic function has exactly one real zero, that zero is a double root of the related equation.

Comparing roots, zeros, and xintercepts • Find the roots, graph the related function and describe the relationship between the roots, the zeros, and the x-intercepts. • x 2 -6 x+9 = 0 • (x-3)= 0 • x-3=0 x= 3 • 3 is the double root- it is the only zero- it is the x-intercept of the graph

practice • 3 x 2+6 x=0 • x 2=-3 x+28 • 4 x 2 +20 x =0 • x 2 -10 x +25=0

Writing a quadratic function, given its zeros • Write a quadratic function that has zeros -5/3 and 1 • Reverse the process of solving a quadratic equation. • • • (x--5/3)(x-1) = 0 (x+5/3)(x-1)=0 3(x+5/3)(x-1)=0(3) (3 x+5)(x-1) = 0 3 x 2 -3 x+5 x-5 = 0 3 x 2 +2 x -5 = 0 so f(x) =3 x 2+2 x-5 has zeros at -5/3 and 1

practice • Write an quadratic function that has zeros -3/2 and 4