Lesson 31 Flowchart and Paragraph Proofs Flowchart Proof

Lesson 31 Flowchart and Paragraph Proofs

Flowchart Proof - A style of proof that uses boxes and arrows to show the structure of the proof. A flowchart proof should be read from left to right or from top to bottom. Each part of the proof appears in a box, while the justification for each step is written under the box. The arrows show the progression of the proof’s steps.

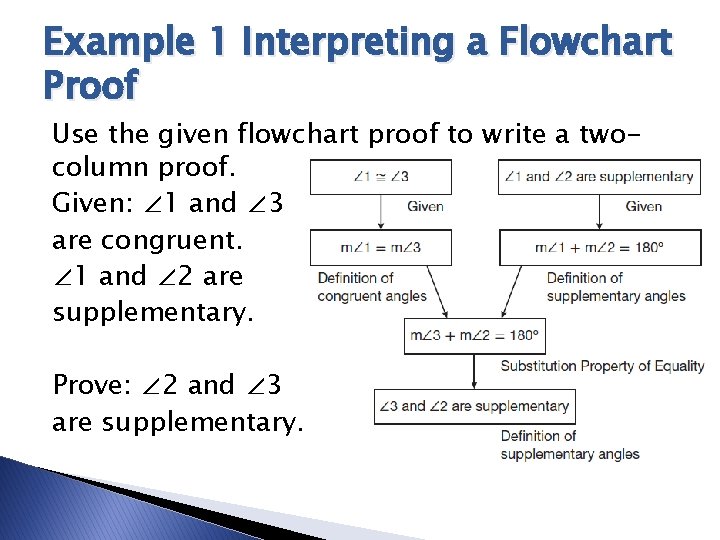
Example 1 Interpreting a Flowchart Proof Use the given flowchart proof to write a twocolumn proof. Given: ∠ 1 and ∠ 3 are congruent. ∠ 1 and ∠ 2 are supplementary. Prove: ∠ 2 and ∠ 3 are supplementary.

Example 1 Interpreting a Flowchart Proof Use the given flowchart proof to write a two-column proof. Given: ∠ 1 and ∠ 3 are congruent. ∠ 1 and ∠ 2 are supplementary. Prove: ∠ 2 and ∠ 3 are supplementary. SOLUTION Write the steps and justifications of the proof as a 2 -column proof. Statements Reasons 1. ∠ 1 and ∠ 3 are congruent. 1. Given 2. ∠ 1 and ∠ 2 are supplementary. 2. Given 3. m∠ 1 = m∠ 3 3. Def of congruent angles 4. m∠ 1 + m∠ 2 = 180° 4. Definition of supp angles 5. m∠ 3 + m∠ 2 = 180° 5. Substitution Prop 6. ∠ 3 and ∠ 2 are supplementary. 6. Definition of supp angles

Flowchart proofs are useful when a proof has two different threads that could be performed at the same time, rather than in sequence with one another. Whenever a proof does not proceed linearly from one step to another, a flowchart proof should be considered.

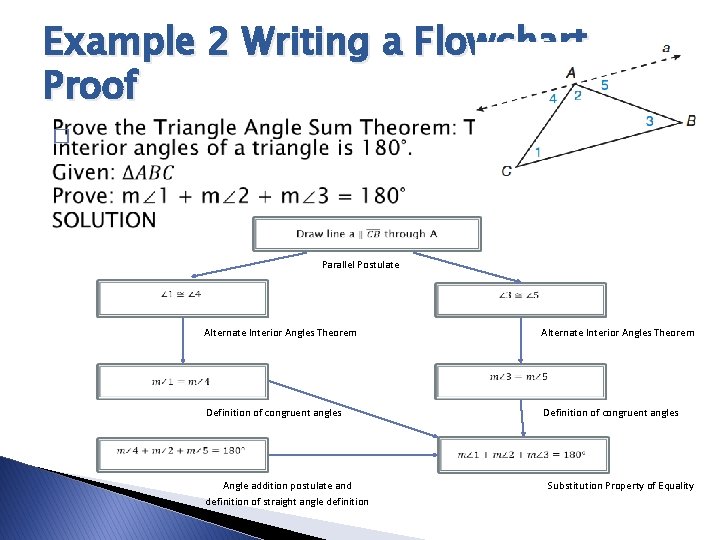
Example 2 Writing a Flowchart Proof � Parallel Postulate Alternate Interior Angles Theorem Definition of congruent angles Angle addition postulate and definition of straight angle definition Substitution Property of Equality

Paragraph Proof - A style of proof in which statements and reasons are presented in paragraph form. In a paragraph proof, every step of the proof must be explained by a sentence in the paragraph. Each sentence contains a statement and a justification.

Example 3 Reading a Paragraph Proof Use the given paragraph proof to write a two-column proof. Given: ∠ 1 and ∠ 2 are complementary. Prove: ∠ 3 and ∠ 4 are complementary. ∠ 1 and ∠ 2 are complementary, so m∠ 1 + m∠ 2 = 90° by the definition of complementary angles. Angle 1 is congruent to ∠ 4, and ∠ 2 is congruent to ∠ 3, by the Vertical Angles Theorem. So m∠ 1 = m∠ 4, and m∠ 2 = m∠ 3. By substitution, m∠ 4 + m∠ 3 = 90°. Therefore, ∠ 3 and ∠ 4 are complementary by the definition of complementary angles. SOLUTION Statements Reasons 1. ∠ 1 and ∠ 2 are complementary. 1. Given 2. m∠ 1 + m∠ 2 = 90° 2. Def of complementary angles 3. ∠ 1 and ∠ 4 are congruent. ∠ 2 and ∠ 3 are congruent. 3. Vertical Angles Theorem 4. m∠ 1 = m∠ 4 and m∠ 2 = m∠ 3 4. Definition of congruent angles 5. m∠ 3 + m∠ 4 = 90° 5. Substitution Property of Equality 6. ∠ 3 and ∠ 4 are complementary. 6. Def of complementary angles

A paragraph proof is good for short proofs where each step follows logically from the one before. Paragraph proofs are usually more compact than two-column proofs.

Example 4 Writing a Paragraph Proof �

You Try! b. Prove the Vertical Angles Theorem using a flowchart proof. Given: a and b are intersecting lines. Prove: ∠ 1 and ∠ 3 are congruent. d. Prove Theorem 5 -4: If two lines are perpendicular, then they form congruent adjacent angles. Given: Lines s and t are perpendicular. Prove: Angles 1 and 2 are congruent adjacent angles.

Assignment Page 200 Lesson Practice (Ask Mr. Heintz) Page 201 Practice 1 -30 (Do the starred ones first)