Lesson 3 Objectives Boundary conditions General Lagrangian solution

Lesson 3 Objectives • • • Boundary conditions General Lagrangian solution (review) Curvilinear coordinate systems • Cylindrical • Sphere Curvilinear Boltzmann Equation Conservative form of curvilinear equations 3 -1

Initial and boundary conditions • In order to solve for the flux y in a volume V of space (with its external surfaces denoted as G) at time t>0, we need to specify two types of external conditions: 1. Initial conditions, 2. Boundary conditions, for all for incoming angles (i. e. , directions for which , where we have followed the usual convention of having be outward-pointing normal vectors on the surface. 3 -2

Initial conditions • The usual situation for specifying initial conditions is to use the solution to the steady -state (i. e. , time-independent) solution Boltzmann at time = 0, that is: where is the solution to: 3 -3

Boundary conditions • The most common boundary conditions are: • Void: • Specified: • (coupled problems) • Reflected: • Periodic: where the points • White: map 3 -4

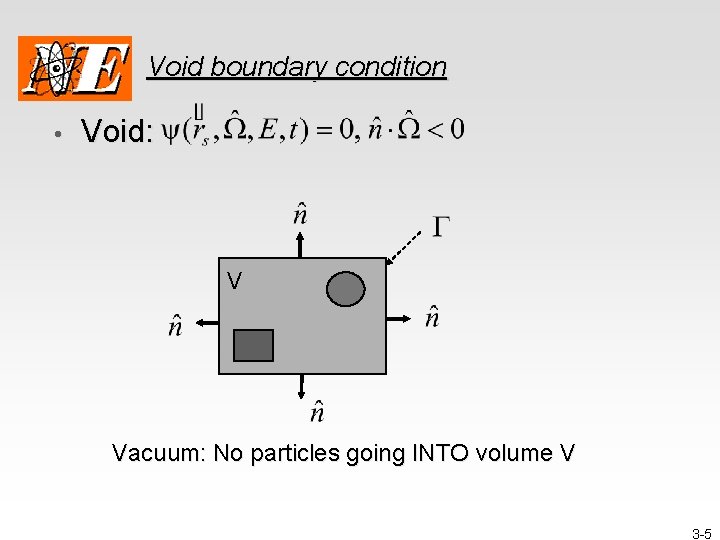
Void boundary condition • Void: V Vacuum: No particles going INTO volume V 3 -5

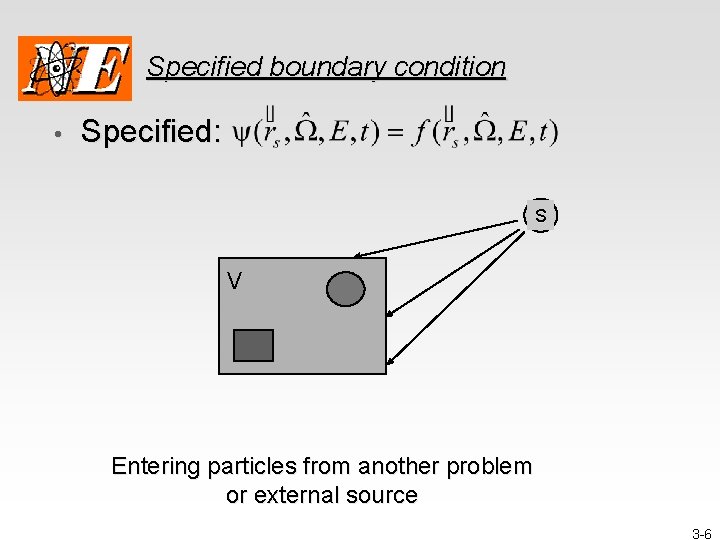
Specified boundary condition • Specified: S V Entering particles from another problem or external source 3 -6

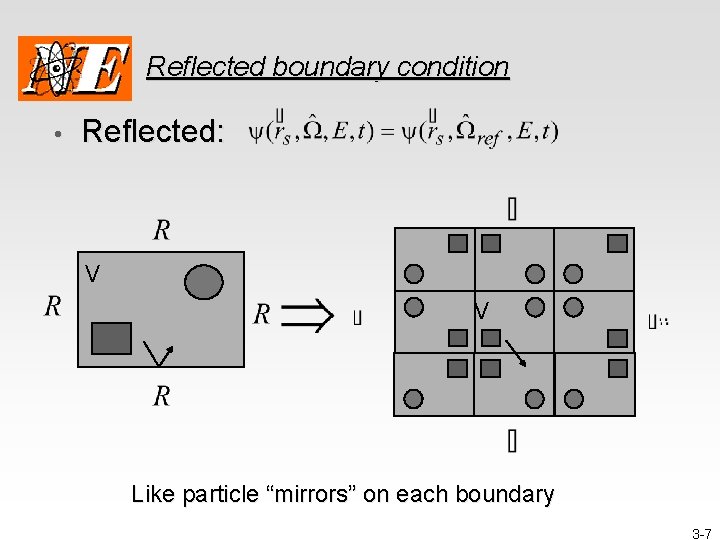
Reflected boundary condition • Reflected: V V Like particle “mirrors” on each boundary 3 -7

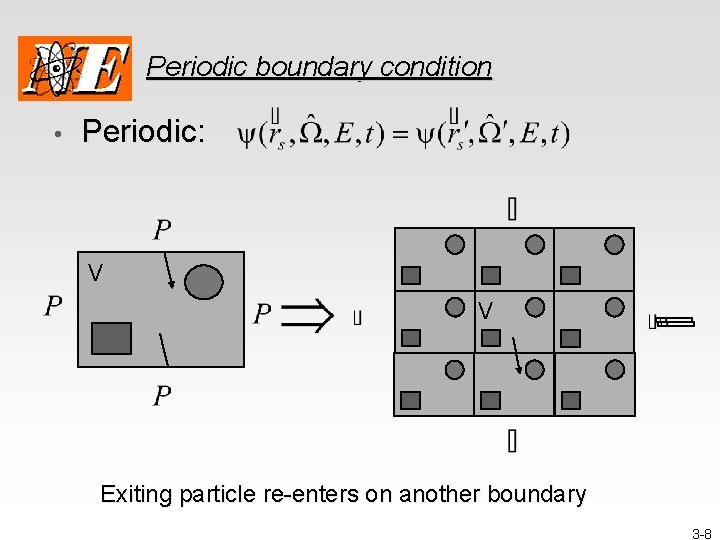
Periodic boundary condition • Periodic: V V Exiting particle re-enters on another boundary 3 -8

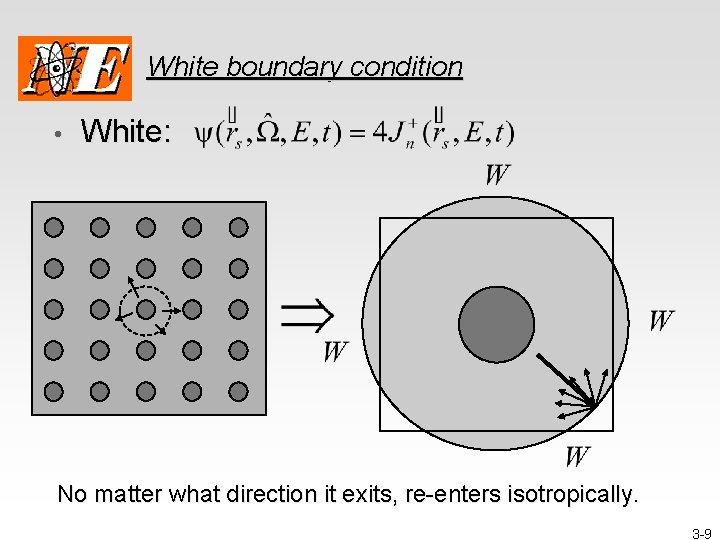
White boundary condition • White: No matter what direction it exits, re-enters isotropically. 3 -9

General Lagrangian solution As you will remember, in the previous lesson we used an Lagrangian frame of reference. • This gave us a solution in the form: • where we defined s as the distance of travel of the particle. 3 -10

General Lagrangian solution (2) • This frame of reference is “moving along with” an unperturbed” pack of particles, and the equation “is completely parameterized” in terms of s: • By “completely parameterized, ” we mean that ALL the variables of y are defined as functions of s. 3 -11

General Lagrangian solution (3) • That is, beginning at some initial u=0, where a particle has some position (x 0, y 0, z 0), direction cosines (m 0 , h 0 , x 0), energy E 0, and age t 0, all of the variable changes can be associated with s. z y x 3 -12

General Lagrangian solution (4) • We evaluate the pieces of the total derivative that are appropriate to the coordinate system: 3 -13

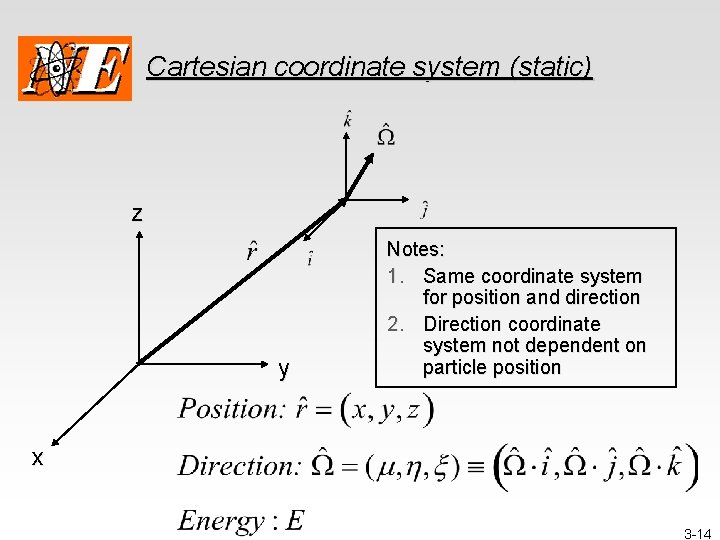
Cartesian coordinate system (static) z y Notes: 1. Same coordinate system for position and direction 2. Direction coordinate system not dependent on particle position x 3 -14

Cartesian coordinate system static (2) 3 -15

2 D Cartesian static • Cartesian geometry can be simplified to 2 D if one dimension can be assumed to be infinite simplifying the flux dependence: • Corresponds to an arrangement of homogenous y rectangular blocks: Note: Infinite in z direction. x 3 -16

2 D Cartesian static (2) 3 -17

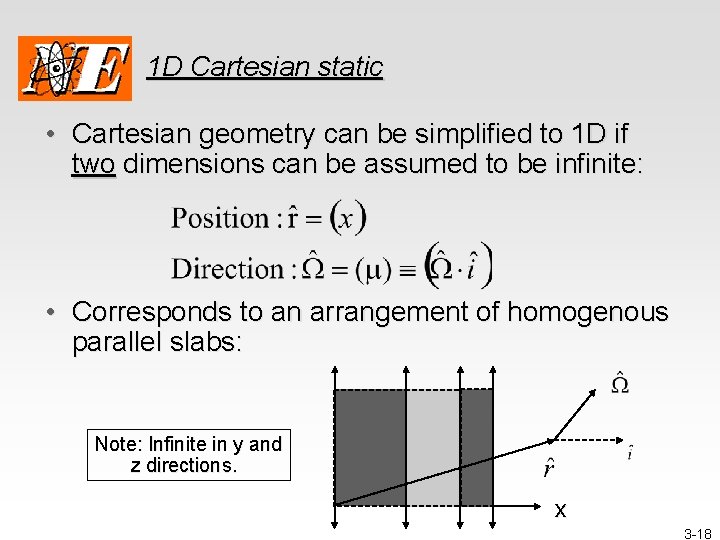
1 D Cartesian static • Cartesian geometry can be simplified to 1 D if two dimensions can be assumed to be infinite: • Corresponds to an arrangement of homogenous parallel slabs: Note: Infinite in y and z directions. x 3 -18

1 D Cartesian static 3 -19

Curvilinear coordinate systems • We have worked out the equation for only ONE of the THREE orthogonal coordinate systems in common use (out of the 13 that have been identified) • The other two are cylindrical and spherical 3 -20

Curvilinear equations • The Boltzmann Equation assumes a different form for the curvilinear (cylindrical and spherical) geometries. • This is because the r vector follows the particle (like a skeet shooter’s rifle). • The result of this is that the direction cosines change as the particle moves, which means that the angular derivatives of the Eulerian solution are no longer 0: 3 -21

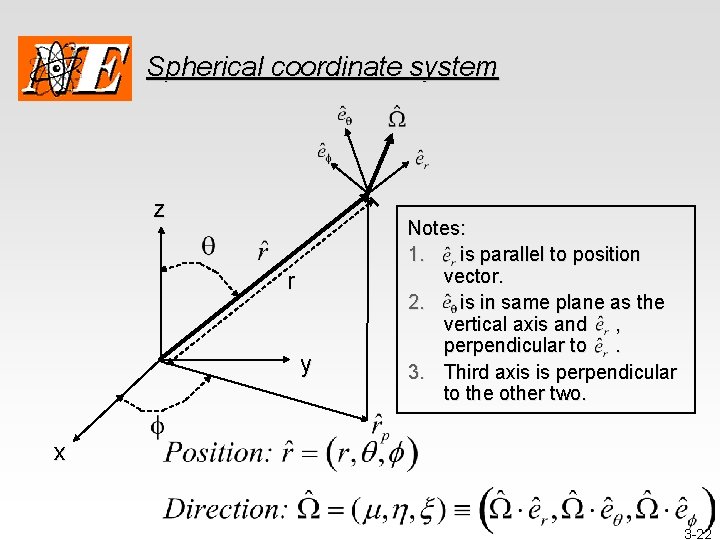
Spherical coordinate system z r y Notes: 1. is parallel to position vector. 2. is in same plane as the vertical axis and , perpendicular to. 3. Third axis is perpendicular to the other two. x 3 -22

Spherical coordinate system 3 -23

1 D spherical • Spherical geometry is usually applied in its 1 D radial form: • Corresponds to a concentric arrangement of spherical shells: 3 -24

1 D spherical • (Losing the azumuthal direction components is actually a little trickier; the eta and xsi terms cancel rather than each being zero) 3 -25

Spherical 1 D curvilinear equations • In spherical 1 D, a close up on the particle is: 3 -26

Spherical 1 D curvilinear equations (2) • Final form of spherical 1 D streaming term: 3 -27

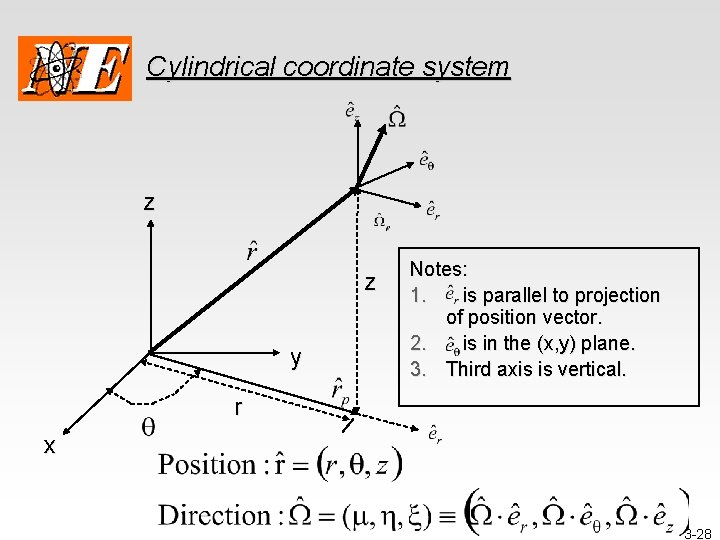
Cylindrical coordinate system z z y Notes: 1. is parallel to projection of position vector. 2. is in the (x, y) plane. 3. Third axis is vertical. r x 3 -28

Cylindrical coordinate system (2) 3 -29

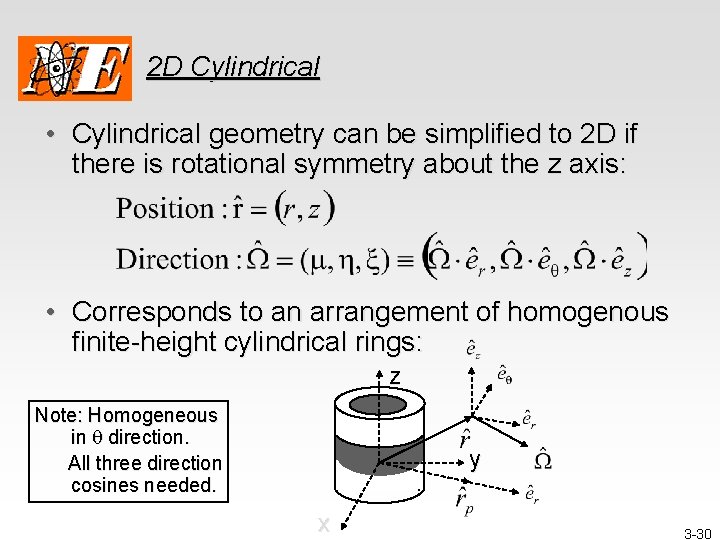
2 D Cylindrical • Cylindrical geometry can be simplified to 2 D if there is rotational symmetry about the z axis: • Corresponds to an arrangement of homogenous finite-height cylindrical rings: z Note: Homogeneous in q direction. All three direction cosines needed. y x 3 -30

1 D Cylindrical • Cylindrical geometry can be simplified to 1 D if there is rotational symmetry about the z axis and homogeneous in z direction: • Corresponds to an arrangement of homogenous infinite-height cylindrical rings: Note: Homogeneous in q and z directions. Two direction variables needed. 3 -31

1 D Cylindrical (2) 3 -32

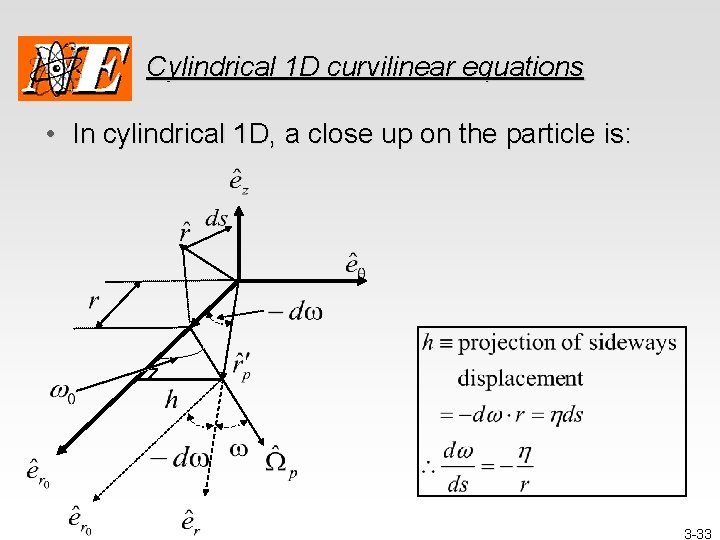
Cylindrical 1 D curvilinear equations • In cylindrical 1 D, a close up on the particle is: 3 -33

Cylindrical 1 D curvilinear equations • Final form of cylindrical 1 D streaming term: 3 -34

Resulting curvilinear 1 D B. E. ’s • The resulting B. E. for the 1 D geometries are: • Cartesian: • Spherical • Cylindrical 3 -35

Conservative form • Having spent all this trouble getting the curvilinear equations, we are NOT going to use them! • Instead we are going to convert them into socalled conservative form, which will be better for us later when we finite difference in space. • For now, I want you to be able to do two things: 1. State why we are doing this: “So that when we finite difference the streaming operator, the resulting terms will conserve particles. ” 2. Show that the two are equivalent. This just involves simple differential calculus. 3 -36

Conservative form for 1 D B. E. ’s • The resulting conservative B. E. ’s for the 1 D curvilinear geometries are: • Spherical • Cylindrical 3 -37

Homework Problems (3 -1) Use the product differentiation rule to show that the conservative and nonconservative forms of the 1 D spherial equation are identical. (3 -2) Use the product differentiation rule to show that the conservative and nonconservative forms of the 1 D cylindrical equation are identical. 3 -38

Homework Problems (2) (3 -3) Show that the white boundary condition is given by: 3 -39