Lesson 3 9 More On Functions Objective Students

Lesson 3 -9: More On Functions Objective Students will: Find composite functions Evaluate composite functions for a given value

Step Functions- a relationship that stays the same value for a set interval then steps up (or down) for the next interval. Example a cell phone’s minutes You may pay $0. 15 per additional minute but what happens if you only talk 10 seconds? You pay for a full minute! What if you talk 5 minutes and 1 sec? You pay for 6 minutes! How would this look when graphed?

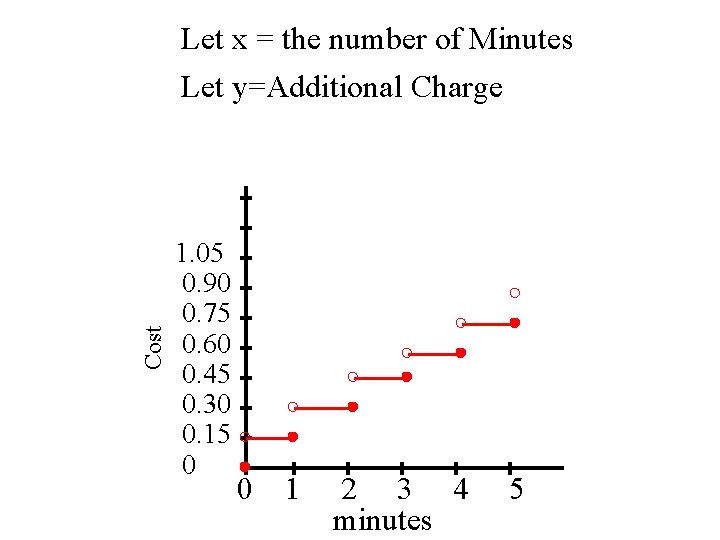
Cost Let x = the number of Minutes Let y=Additional Charge 1. 05 0. 90 0. 75 0. 60 0. 45 0. 30 0. 15 0 0 1 2 3 4 minutes 5

Questions: 1)Why is is referred to as a “step” function 2)For this example why are the negative quadrants not visible? 3) Why is the an open and closed circle at each integer?

Greatest Integer Function (another step function): notated y = [x] means: the greatest integer that is less than or equal to x Ex: [4. 6] = 4 [-1] = -1 [-2. 8] = -3 Graph this function: Hint: think about where the function is opened or closed.

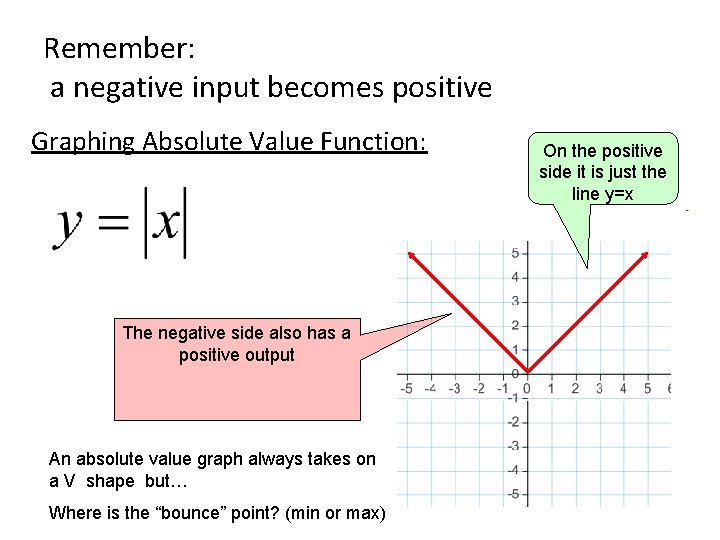
Remember: a negative input becomes positive Graphing Absolute Value Function: The negative side also has a positive output An absolute value graph always takes on a V shape but… Where is the “bounce” point? (min or max) On the positive side it is just the line y=x

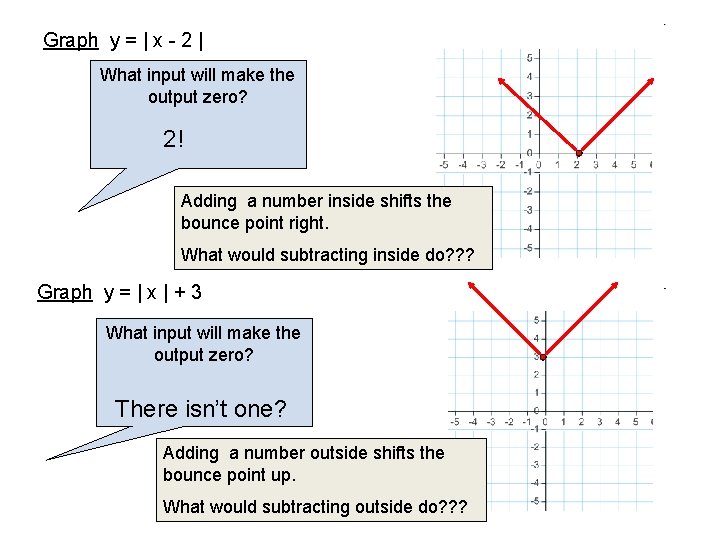
Graph y = | x - 2 | What input will make the output zero? 2! Adding a number inside shifts the bounce point right. What would subtracting inside do? ? ? Graph y = | x | + 3 What input will make the output zero? There isn’t one? Adding a number outside shifts the bounce point up. What would subtracting outside do? ? ?

Predict What would the graph of Look like?

Composite Functions §Combination of 2 or more functions like: f(x) and g(x) §Written: f(g(x)) → g(x) replaces x §Plug one function into x in the other §Since f is on outside g goes into the f function f(x) = x + 2 g(x) = 3 x f(g(x)) = 3 x + 2 Evaluating Composites §Plugging in a number for the variable § 2 choices 1) Evaluate f(g(x)) first → then plug in the value (like above) f(g(5))= 3(5) +2 =17 2) Plug the number in g(x) first – evaluate; plug this number into f(x) – evaluate

2) Plug the number in g(x) first – evaluate; plug this number into f(x) – evaluate f(g(5))= g(5) = 3(5) = 15 f(15) = 15+2 =17 You get the same answer either way!!!

You Try 1: f(x) = 2 x – 1 , g(x) = 5 x; find f(g(x)) You Try 2: g(x) = x 2 – 1 , h(x) = x + 2; find g(h(x)); find g(h(3)) Hmmm… This one is challenging