Lesson 3 7 continued Objectives Graphing Absolute Value

Lesson 3. 7 continued Objectives: Graphing Absolute Value Functions. Lesson Recap: Absolute value function: A function that contains an absolute value equation. The Parent function for an absolute value function is y=|x| Parent function: A set of basic function used as building blocks for more complicated functions. Ex. : abs. value funct. : y=|x| f(x)=|x-h| f(x)=|x|+k Vertex: The point where the graph changes direction. The VERTEX of the parent absolute value function y= |x| is (0, 0) or the origin. Translating graphs: Stretching a Graph: The rigid movement of a function vertically or horizontally. A graph that is stretched results in a narrower graph Shrinking a Graph: A graph that is shrunk results in a wider graph Reflecting a Graph: A graph that is reflected results in a graph that is mirrored over the x-axis

Vocabulary Vertex form: When an Absolute Value Function is written in the form: g(x) = a | x – h | + k where a ≠ 0. The vertex of the graph of g is ( h , k ) Note: Any absolute value function can be written in VERTEX FORM and its graph is symmetric about the vertical line x = h. Essential Question #1 How do you graph an absolute value function when it is vertex form ( g(x) = a | x – h | + k )? Solve & Graph #1: g(x) = | x + 2| - 3 Solve & Graph #2: f(x) = - | x + 2 | - 3 Solve & Graph #3: g(x) = | x - 2| + 3 Solve & Graph #4: f(x) = - | x - 2 | + 3

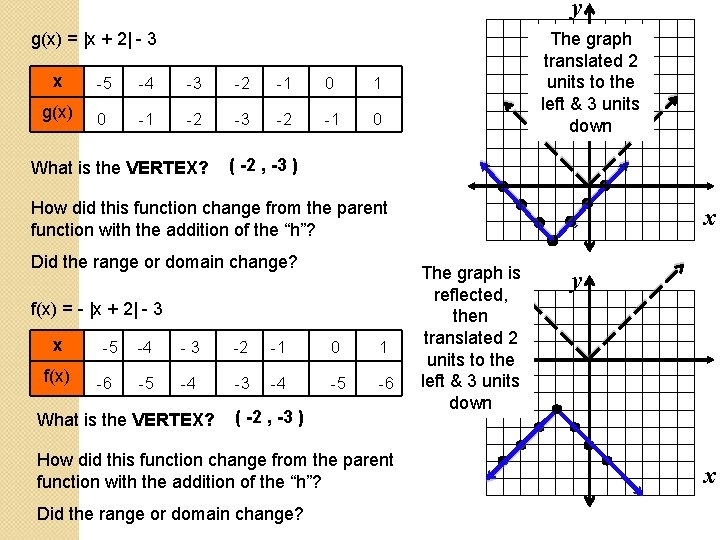
y The graph translated 2 units to the left & 3 units down g(x) = |x + 2| - 3 x -5 -4 -3 -2 -1 0 1 g(x) 0 -1 -2 -3 -2 -1 0 What is the VERTEX? ( -2 , -3 ) How did this function change from the parent function with the addition of the “h”? Did the range or domain change? f(x) = - |x + 2| - 3 x f(x) -5 -6 -4 -3 -2 -1 0 1 -5 -4 -3 -4 -5 -6 What is the VERTEX? ( -2 , -3 ) How did this function change from the parent function with the addition of the “h”? Did the range or domain change? x The graph is reflected, then translated 2 units to the left & 3 units down y x

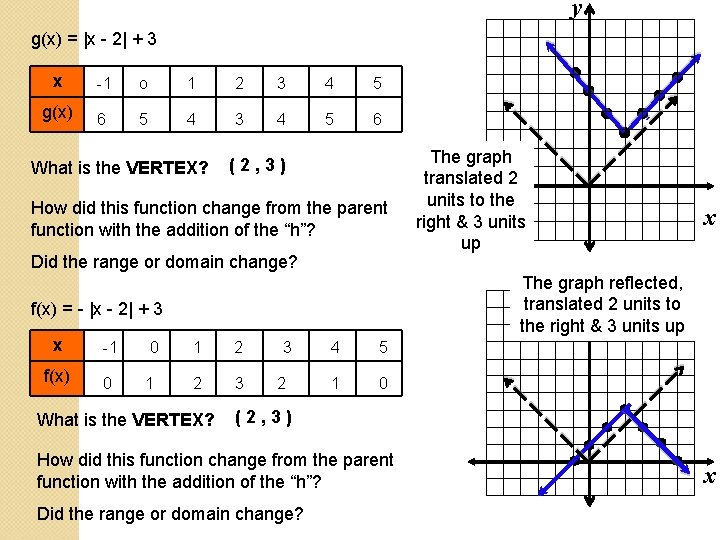
y g(x) = |x - 2| + 3 x -1 o 1 2 3 4 5 g(x) 6 5 4 3 4 5 6 What is the VERTEX? (2, 3) How did this function change from the parent function with the addition of the “h”? Did the range or domain change? -1 0 1 2 f(x) 0 1 2 3 What is the VERTEX? 3 2 x y reflected, The graph translated 2 units to the right & 3 units up f(x) = - |x - 2| + 3 x The graph translated 2 units to the right & 3 units up 4 5 1 0 (2, 3) How did this function change from the parent function with the addition of the “h”? Did the range or domain change? x

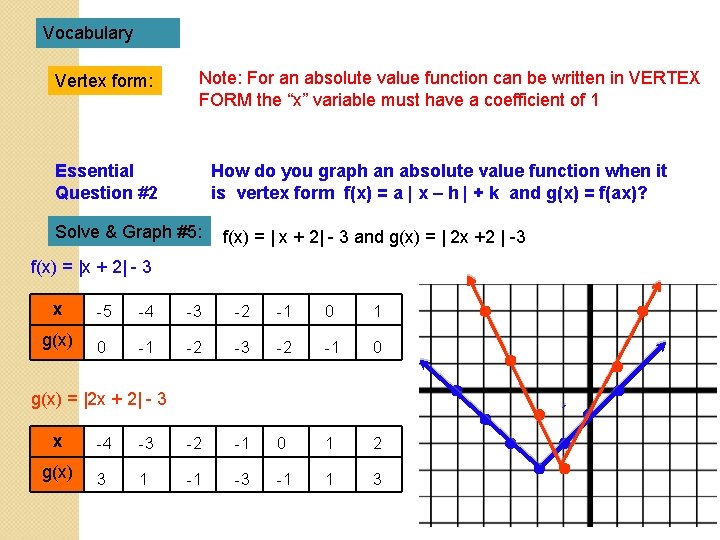
Vocabulary Vertex form: Note: For an absolute value function can be written in VERTEX FORM the “x” variable must have a coefficient of 1 Essential Question #2 How do you graph an absolute value function when it is vertex form f(x) = a | x – h | + k and g(x) = f(ax)? Solve & Graph #5: f(x) = | x + 2| - 3 and g(x) = | 2 x +2 | -3 f(x) = |x + 2| - 3 x -5 -4 -3 -2 -1 0 1 g(x) 0 -1 -2 -3 -2 -1 0 g(x) = |2 x + 2| - 3 x -4 -3 -2 -1 0 1 2 g(x) 3 1 -1 -3 -1 1 3

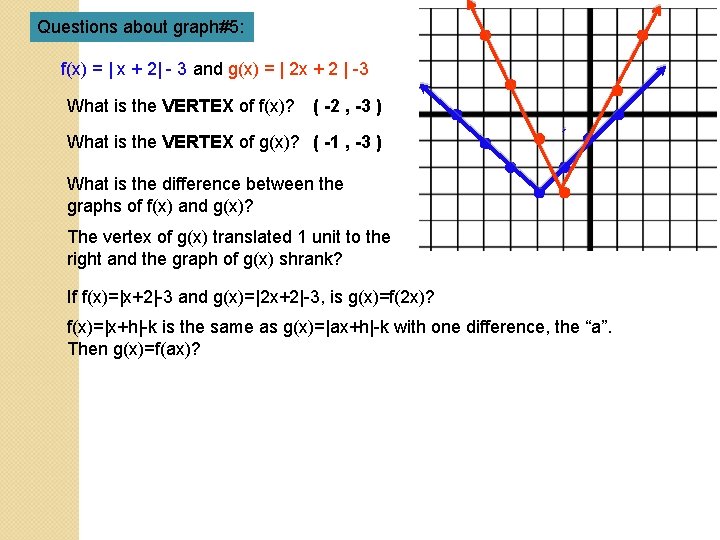
Questions about graph#5: f(x) = | x + 2| - 3 and g(x) = | 2 x + 2 | -3 What is the VERTEX of f(x)? ( -2 , -3 ) What is the VERTEX of g(x)? ( -1 , -3 ) What is the difference between the graphs of f(x) and g(x)? The vertex of g(x) translated 1 unit to the right and the graph of g(x) shrank? If f(x)=|x+2|-3 and g(x)=|2 x+2|-3, is g(x)=f(2 x)? f(x)=|x+h|-k is the same as g(x)=|ax+h|-k with one difference, the “a”. Then g(x)=f(ax)?

Additional Practice x f(x) = | x – 1 | and g(x) = | ½ x – 1 | x g(x)

Additional Practice x f(x) = | x + 2 | + 2 and g(x) = | -4 x + 2 | + 2 x g(x)

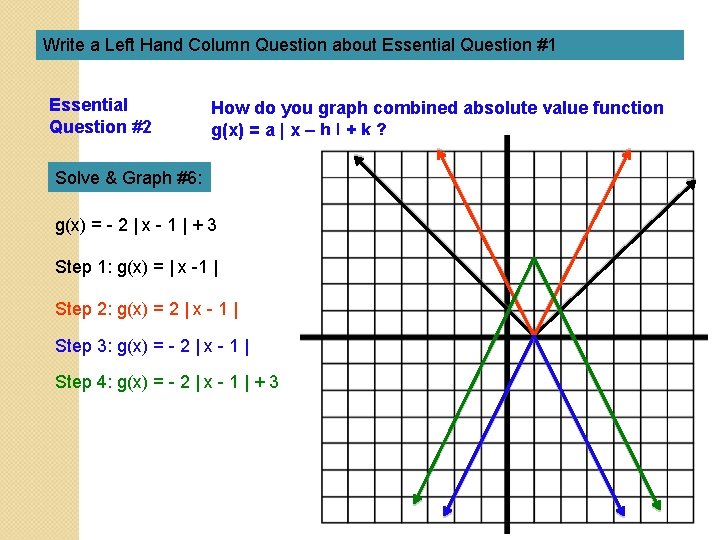
Write a Left Hand Column Question about Essential Question #1 Essential Question #2 How do you graph combined absolute value function g(x) = a | x – h | + k ? Solve & Graph #6: g(x) = - 2 | x - 1 | + 3 Step 1: g(x) = | x -1 | Step 2: g(x) = 2 | x - 1 | Step 3: g(x) = - 2 | x - 1 | Step 4: g(x) = - 2 | x - 1 | + 3

g(x) = - 2 | x – 1 | + 3 x -3 -2 -1 0 1 2 3 g(x) -5 -3 -1 1 3 1 -1 What is the VERTEX? (1, 3) How did this function change from the parent function? Did the range or domain change? The graph translated 1 units to the right, reflected, stretched & translated 3 units up

Write a Left Hand Column Question about Essential Question #2 Have we answered all essential questions? Write a summary about graphing absolute value functions (complete 3. 7)