Lesson 3 6 Ratios and Proportions Objectives I

Lesson 3 -6: Ratios and Proportions

Objectives - I can determine if two fractions form a proportion - I can solve a proportion

Don’t forget to get graph paper for Chapter Four. Coming soon to an Algebra Class near you!!!

Vocabulary • Ratio – Comparison of 2 numbers x to y x: y

Vocabulary • Ratio – Comparison of 2 numbers • Proportion – Equation stating that 2 ratios are equal

Example 1 Determine whether the following ratios form a proportion. 0. 25 2

Example 1 Determine whether the following ratios form a proportion. 0. 25 2 = 0. 5 1. 25 0. 6

Example 1 Determine whether the following ratios form a proportion. 0. 25 2 = 0. 5 1. 25 0. 6 = 0. 75

Example 1 Determine whether the following ratios form a proportion. 0. 25 2 = 0. 5 1. 25 0. 6 = 0. 75 No

• Cross Multiply -

• Cross Multiply – If Then

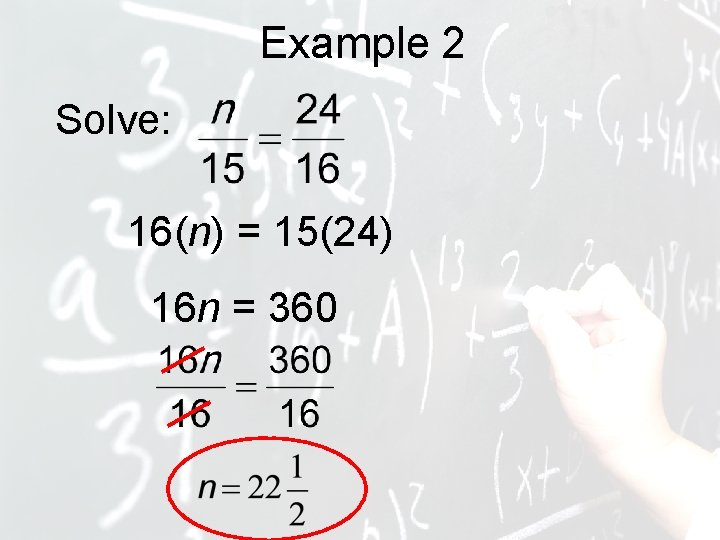
Example 2 Solve: 16(n) = 15(24) 16 n = 360

Example 3 The gear on a bicycle is 8: 5. This means that for every 8 turns of the pedals, the wheel turns 5 times. Suppose the bicycle wheel turns about 2435 times during a trip. How many times would you have to crank the pedals during the trip? 5 p = 8(2435)

Example 3 The gear on a bicycle is 8: 5. This means that for every 8 turns of the pedals, the wheel turns 5 times. Suppose the bicycle wheel turns about 2435 times during a trip. How many times would you have to crank the pedals during the trip? 5 p = 8(2435) 5 p = 19, 480

Example 3 The gear on a bicycle is 8: 5. This means that for every 8 turns of the pedals, the wheel turns 5 times. Suppose the bicycle wheel turns about 2435 times during a trip. How many times would you have to crank the pedals during the trip? 5 p = 8(2435) 5 p = 19, 480 5 5

Example 3 The gear on a bicycle is 8: 5. This means that for every 8 turns of the pedals, the wheel turns 5 times. Suppose the bicycle wheel turns about 2435 times during a trip. How many times would you have to crank the pedals during the trip? 5 p = 8(2435) 5 p = 19, 480 5 5 p = 3896 times

Example 4 In a road atlas, the scale for the map of Connecticut is 5 inches = 41 miles. What is the distance in miles represented by 2½ inches on the map? 5 m = 2½(41) 5 m = 102½

Example 4 In a road atlas, the scale for the map of Connecticut is 5 inches = 41 miles. What is the distance in miles represented by 2½ inches on the map? 5 m = 2½(41) 5 m = 102½ 5 5

Example 4 In a road atlas, the scale for the map of Connecticut is 5 inches = 41 miles. What is the distance in miles represented by 2½ inches on the map? 5 m = 2½(41) 5 m = 102½ 5 5 m = 20½ miles

Homework Pgs. 158 -159: 12 -54 Evens Omit 18 & 36