Lesson 3 6 Ratios and Proportions Objectives Determine

Lesson 3 -6 Ratios and Proportions

Objectives • Determine whether two ratios form a proportion • Solve proportions

Vocabulary • Ratio – a comparison of two numbers by division • Proportion – an equation stating that two ratios are equal • Extremes – the large and small numbers in a proportion • Means – the middle numbers in a proportion • Rate – ration of two measurements with different units of measure • Scale – ratio or rate using in modeling

Four Step Problem Solving Plan • Step 1: Explore the Problem – Identify what information is given (the facts) – Identify what you are asked to find (the question) • Step 2: Plan the Solution – Find an equation the represents the problem – Let a variable represent what you are looking for • Step 3: Solve the Problem – Plug into your equation and solve for the variable • Step 4: Examine the Solution – Does your answer make sense? – Does it fit the facts in the problem?

Example 1 Determine whether the ratios proportion. and form a Answer: The ratios are equal. Therefore, they form a proportion.

Example 2 Use cross products to determine whether the pair of ratios below forms a proportion. Write the equation. Find the cross products. Simplify. Answer: The cross products are not equal, so the ratios do not form a proportion.

Example 3 Solve the proportion . Original equation Find the cross products. Simplify. Divide each side by 8. Answer: Simplify.

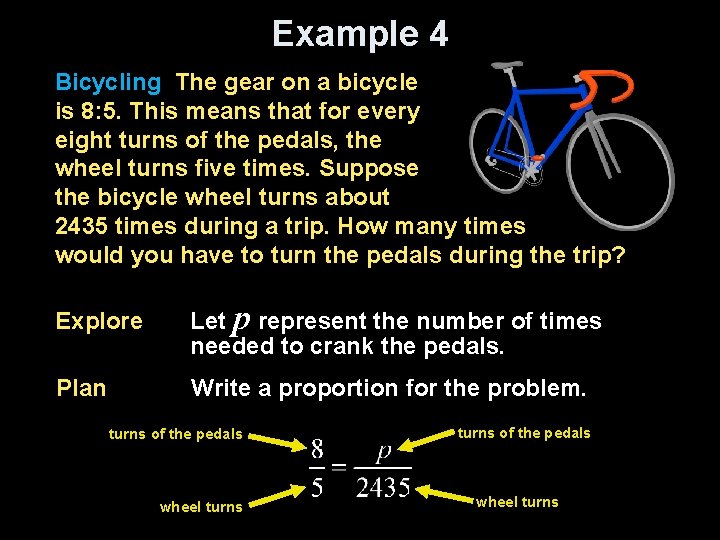
Example 4 Bicycling The gear on a bicycle is 8: 5. This means that for every eight turns of the pedals, the wheel turns five times. Suppose the bicycle wheel turns about 2435 times during a trip. How many times would you have to turn the pedals during the trip? Explore Let p represent the number of times needed to crank the pedals. Plan Write a proportion for the problem. turns of the pedals wheel turns

Example 4 cont Solve Original proportion Find the cross products. Simplify. Divide each side by 5. Answer: 3896 = p Simplify.

Example 5 The scale on a map of the United States is 1 and 3/8 inches = 750 miles. The distance, on the map, between Los Angeles and Washington, D. C. , is about 3 and 7/8 inches. What is the distance in miles between the two locations? changing fractions map scale 1 3/8 in. ------ = 750 miles 3 7/8 in ------d miles cross multiplication 11/8 in. ------ = 750 miles 31/8 in ------d miles multiply by inverse 11/8 d = 31/8 (750) d = (8/11) (31/8) (750) cancel 8’s out d = (31/11) (750) = 2, 113. 64 miles Answer: The distance in miles between Los Angeles and Washington, D. C. , is about 2, 114 miles.

Summary & Homework • Summary: – A ratio is a comparison of two numbers by division – A proportion is an equation stating that two ratios are equal – A proportion can be solved by finding the cross products – Remember the distributive property! • Homework: – pg 158: 12 -32 even