Lesson 3 5 Identifying Solutions Concept Identifying Solutions

Lesson 3. 5 Identifying Solutions Concept: Identifying Solutions EQ: How do we identify and interpret the solutions of an equation f(x) = g(x)? Standard: REI. 10 -11 Vocabulary: Expenses, Income, Profit, Break-even point

Let’s Review A solution to a system of equations is a value that makes both equations true. (-1, -3) y=-x -4 y=2 x -1 -3=-(-1) -4 ✓ -3=-3 -3=2(-1) -1 -3= -2 -1 -3= -3 ✓

Let’s Review The point where two lines intersect is a solution to both equations. In real world problems, 25 we are often only 20 concerned with the xcoordinate. 15 10 5 0 0 1 2 3 4 5 6

Let’s Review Remember that in real-world problems, the slope of the equation is the amount that describes the rate of change, and the y-intercept is the amount that represents the initial value. For business problems that deal with making a profit, the break-even point is when the expenses and the income are equal. In other words you don’t make money nor lose money…your profit is $0.

Let’s Review Words to know for any business problems: § Expenses - the money spent to purchase your product or equipment § Income - the total money obtained from selling your product. § Profit - the expenses subtracted from the income. § Break-even point - the point where the expenses and the income are equal. In other words you don’t make money nor lose money…your profit is $0.

In this lesson you will learn to find the x-coordinate of the intersection of two linear functions in three different ways: 1. By observing their graphs 2. Making a table 3. Setting the functions equal to each other (algebraically)

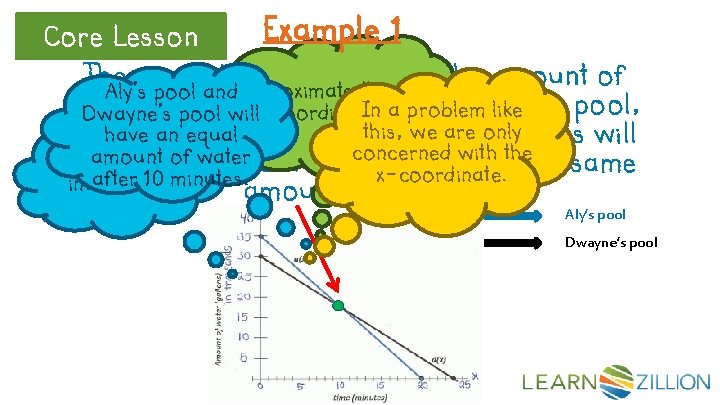
Core Lesson Example 1 Aly and Dwayne work at a water park and have to drain the water from the small pool at the bottom of their ride at the end of the month. Each uses a pump to remove the water. Aly’s pool has 35, 000 gallons of water in it and drains at a rate of 1, 750 gallons a minute. Dwayne’s pool has 30, 000 gallons of water in it and drains at a rate of 1, 000 gallons a minute. After approximately how many minutes will Aly and Dwayne’s pools have the same amount of water in them?

Core Lesson Example 1 Aly’s pool has 35, 000 gallons of water in it and drains at a rate of 1, 750 gallons a minute. Dwayne’s pool has 30, 000 gallons of water in it and drains at a rate of 1, 000 gallons a minute. After approximately how many minutes will Aly and Dwayne’s pools have the same amount of water in them?

Core Lesson We need to write 2 equations! Example 1 slope First we can identify our slope and y-intercept Aly’s pool has 35, 000 gallons of water in it and Both of of the slopes drains at a rate 1, 750 gallons a minute. will be negative Dwayne’s pool has 30, 000 gallons of water in it because the water is leaving the and drains at a rate of 1, 000 gallons a minute. y-intercept pools. slope x=# of minutes; a(x) & d(x)=amount of water left in pool Aly’s a(x)= -1, 750 x + 35, 000 Dwayne’s d(x)= -1, 000 x + 30, 000

Core Lesson Example 1 The graph below represents the amount of Aly’s pool and. Approximate the x water in pool Aly’swill pool, a(x), and Dwayne’s pool, In a problem like -coordinate. Dwayne’s this, we are only have an equal d(x), over time. After how many minutes will concerned with the amount ofofwater Find the point Aly’s pool and Dwayne’s pool have the same x-coordinate. after 10 minutes. intersection. amount of water? Aly’s pool Dwayne’s pool

Core Lesson Example 1 Here, the graph helps us solve, but graphing can also help us to estimate the solution. Can you think of a problem where an approximation might be sufficient? Aly’s Pool Dwayne’s Pool

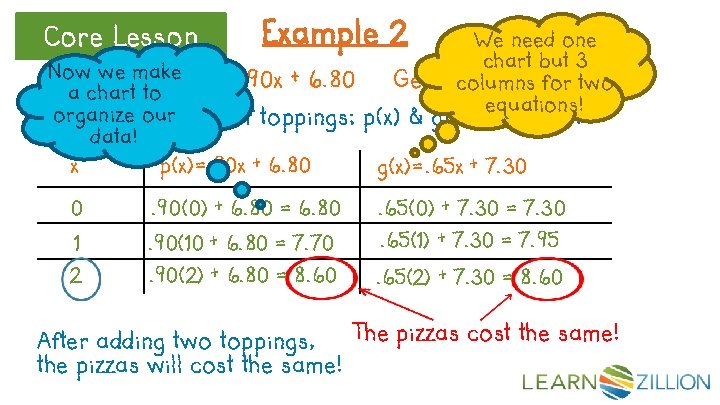
Core Lesson We need to y-intercept write 2 equations! Example 2 slope First we can identify our slope Paradiseand Pizzeria costs y-intercept. A large cheese pizza at $6. 80 plus $0. 90 for each topping. The cost of a large cheese pizza at Geno’s Pizza is $7. 30 plus $0. 65 for each topping. How many toppings need to be added to a large cheese pizza from Paradise and Geno’s in order for the pizzas to cost the same, not including tax? y-intercept slope Paradise p(x)=. 90 x + 6. 80 Geno’s g(x)=. 65 x + 7. 30

Core Lesson Example 2 We need one chart but 3 Geno’scolumns g(x)=. 65 x 7. 30 for +two equations! Now we make Paradise p(x)=. 90 x + 6. 80 a chart to organize our x=# of toppings; p(x) & g(x)=total cost data! x p(x)=. 90 x + 6. 80 g(x)=. 65 x + 7. 30 0 . 90(0) + 6. 80 = 6. 80 . 65(0) + 7. 30 = 7. 30 1 . 90(10 + 6. 80 = 7. 70 . 65(1) + 7. 30 = 7. 95 2 . 90(2) + 6. 80 = 8. 60 . 65(2) + 7. 30 = 8. 60 The pizzas cost the same! After adding two toppings, the pizzas will cost the same!

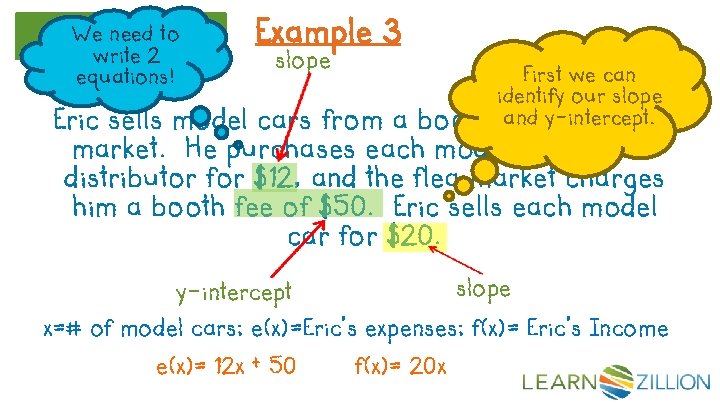
Core Lesson Example 3 Eric sells model cars from a booth at a local flea market. He purchases each model car from a distributor for $12, and the flea market charges him a booth fee of $50. Eric sells each model car for $20. How many model cars must Eric sell in order to reach the break-even point?

We need to Core Lesson write 2 equations! Example 3 slope First we can identify our slope anday-intercept. at local flea Eric sells model cars from a booth market. He purchases each model car from a distributor for $12, and the flea market charges him a booth fee of $50. Eric sells each model car for $20. slope y-intercept x=# of model cars; e(x)=Eric’s expenses; f(x)= Eric’s Income e(x)= 12 x + 50 f(x)= 20 x

Core Lesson Example 3 Eric’s Expenses e(x)=12 x + 50 Eric’s Income f(x)=20 x Since both e(x) and f(x) are equal to “y”, Eric needs to sell more can than 6 model you set the equations equal to each other cars to break even!and solve for “x”. e(x) = f(x) 12 x + 50 = 20 x 50 = 8 x 6. 25 = x

Core Lesson Example 3 Eric’s Expenses e(x)=12 x + 50 Eric’s Income f(x)=20 x How can we write a function to = represent Income. Eric’s – Expenses Profit? Profit So take the two given functions and subtract them. P(x) = f(x) – e(x) P(x) = 20 x – (12 x + 50) P(x) = 8 x - 50

Core Lesson You Try 1 – Solve using graphing Chen starts his own lawn mowing business. He initially spends $180 on a new lawnmower. For each yard he mows, he receives $20 and spends $4 on gas. If x represents the # of lawns, then let Chen’s expenses be modeled by the function m(x)=4 x + 180 and his income be modeled by the function p(x) = 20 x How many lawns must Chen mow to break-even?

You Try 2 – Solve using a table Core Lesson Olivia is building birdhouses to raise money for a trip to Hawaii. She spends a total of $30 on the tools needed to build the houses. The material to build each birdhouse costs $3. 25. Olivia sells each birdhouse for $10. If x represents the # of birdhouses, then let Olivia’s expenses be modeled by the function b(x)=3. 25 x + 30 and her income be modeled by the function p(x) = 10 x How many birdhouses must Olivia sell to break-even?

Core Lesson You Try 3 – Solve using algebra Text Away cell phone company charges a flat rate of $30 per month plus $0. 20 per text. It’s Your Dime cell phone company charges a flat rate of $20 per month plus $0. 40 per text. If x represents the # of texts, then let your Text Away bill be modeled by the function t(x)=. 20 x + 30 and Your Dime bill be modeled by the function d(x) =. 40 x + 20 How many texts must you send before your bill for each company will be the same?