LESSON 3 3 Interpreting the Unit Rate as

Texas Essential Knowledge and Skills The student is expected to: Proportionality— 8. 4. B

ADDITIONAL EXAMPLE 1 Every 10 seconds an escalator step rises 6 feet. Draw a

ADDITIONAL EXAMPLE 2 The equation y = 1. 2 x represents the rate, in

3. 3 LESSON QUIZ 8. 4. B, 8. 4. C 1. Every 4 seconds,

2. Under Plan A, a 2 -minute call costs $0. 54 and a 4

3. The equation y = 13 x represents the rate, in gallons per minute,

Have students select any of the proportional relationships in the lesson, given as an

Then have them classify which operations kept the proportional relationship and which did not.

How do you interpret the unit rate as slope? Sample answer: The ratio of

Slides: 10

Download presentation

LESSON 3. 3 Interpreting the Unit Rate as Slope How do you interpret the unit rate as slope?

Texas Essential Knowledge and Skills The student is expected to: Proportionality— 8. 4. B Graph proportional relationships, interpreting the unit rate as the slope of the line that models the relationship. Proportionality— 8. 4. C Use data from a table or graph to determine the rate of change or slope and y-intercept in mathematical and real-world problems. Mathematical Processes 8. 1. F Analyze mathematical relationships to connect and communicate mathematical ideas.

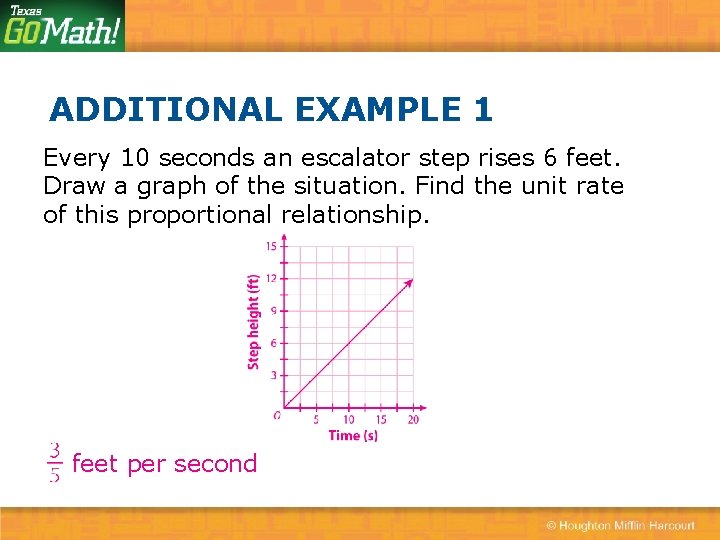
ADDITIONAL EXAMPLE 1 Every 10 seconds an escalator step rises 6 feet. Draw a graph of the situation. Find the unit rate of this proportional relationship. feet per second

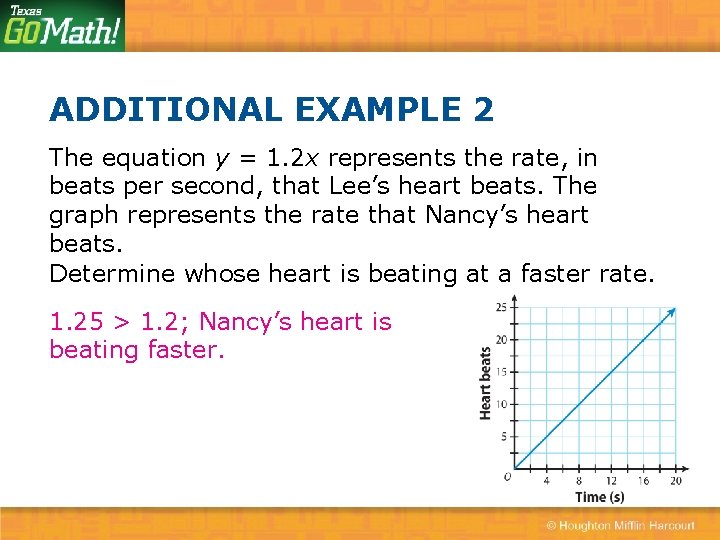
ADDITIONAL EXAMPLE 2 The equation y = 1. 2 x represents the rate, in beats per second, that Lee’s heart beats. The graph represents the rate that Nancy’s heart beats. Determine whose heart is beating at a faster rate. 1. 25 > 1. 2; Nancy’s heart is beating faster.

3. 3 LESSON QUIZ 8. 4. B, 8. 4. C 1. Every 4 seconds, a ski lift chair rises 14 feet. Draw a graph of the situation. Then describe the relationship between the height of the chair and the time. The unit rate of the height of the chair is feet per second.

2. Under Plan A, a 2 -minute call costs $0. 54 and a 4 -minute call costs $1. 08. Under Plan B, the cost for x minutes is given by y = 0. 289 x. Which plan is cheaper? Why? Plan A; $0. 27/min < $0. 289/min

3. The equation y = 13 x represents the rate, in gallons per minute, that Tank A at an aquarium fills with water. The table represents the rate that Tank B fills with water. Determine which tank fills faster. Tank A; 13 gal/min > 11 gal/min

Have students select any of the proportional relationships in the lesson, given as an equation, table, or graph. Then have them consider whethere is still a proportional relationship if each of these operations is performed on the y-values. • double the y-values yes • divide the y-values by 10 • add 5 to the y-values yes no • subtract 5 from the y-values no

Then have them classify which operations kept the proportional relationship and which did not. Multiplication and division preserve the proportional relationship; addition and subtraction do not.

How do you interpret the unit rate as slope? Sample answer: The ratio of the change in y to the change in x is the unit rate. It is also the ratio of the rise to the run, or the slope.