Lesson 3 1 Parallel Lines and Transversals Students

Lesson 3. 1 Parallel Lines and Transversals Students will be able to describe angles formed by parallel lines and transversals

Youtube https: //www. youtube. com/watch? v=Tz. Tr 5 zbg 3 t E

Answer these questions in your notebook: 1) What does it mean for two lines to be parallel? What are some properties of two parallel lines?

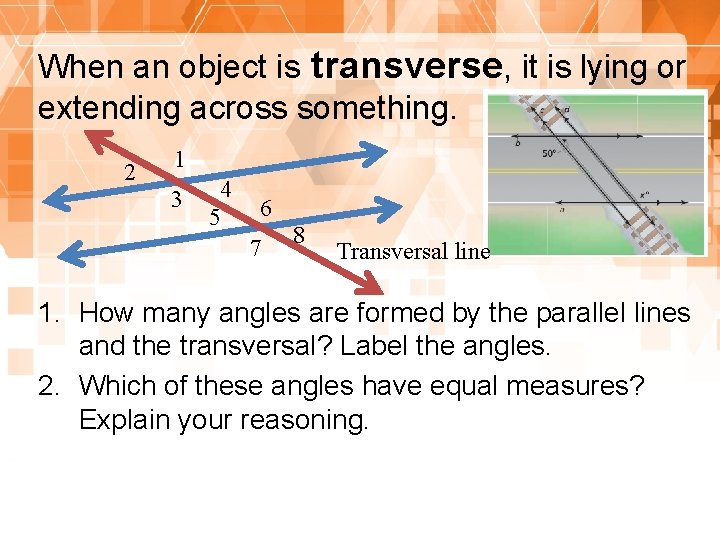
When an object is transverse, it is lying or extending across something. 2 1 3 4 5 6 7 8 Transversal line 1. How many angles are formed by the parallel lines and the transversal? Label the angles. 2. Which of these angles have equal measures? Explain your reasoning.

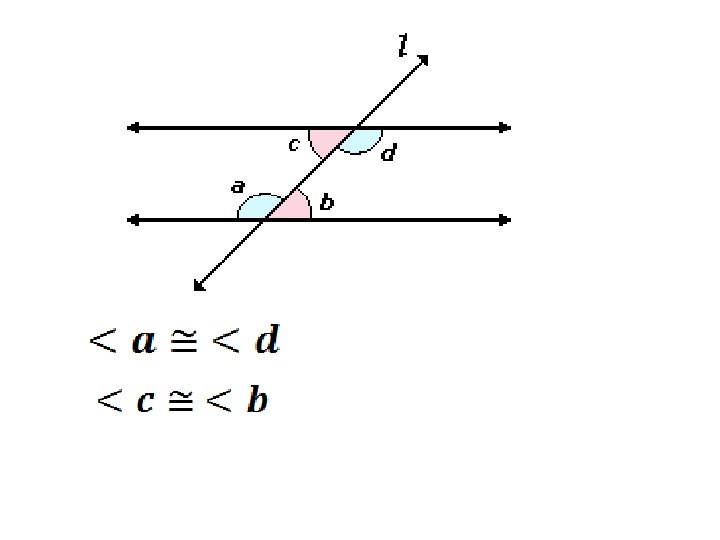
Transversal: a line that intersect two or more lines. When parallel lines are cut by a transversal, several pairs of congruent angles are formed.

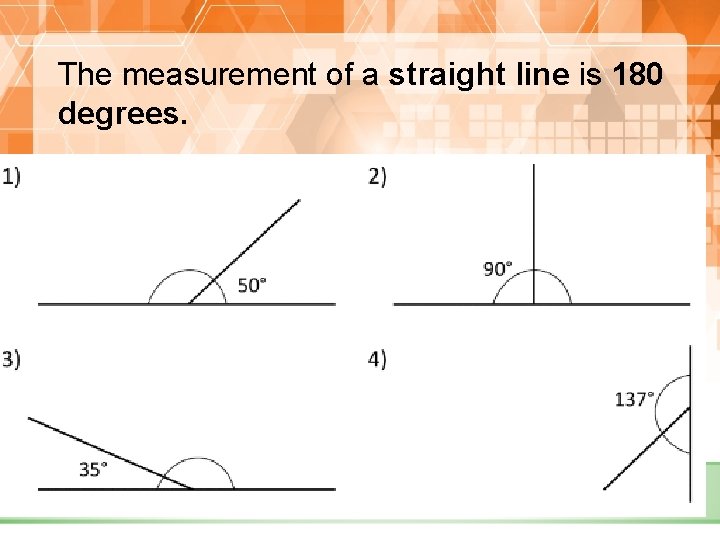
The measurement of a straight line is 180 degrees.

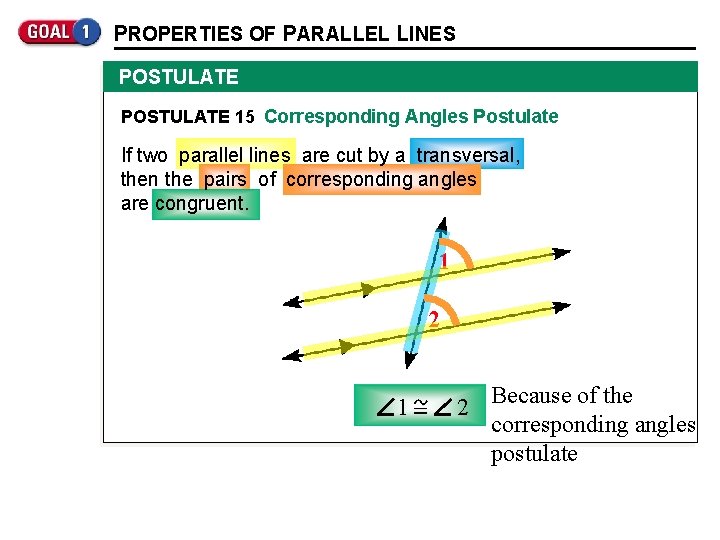
PROPERTIES OF PARALLEL LINES POSTULATE 15 Corresponding Angles Postulate If two parallel lines are cut by a transversal, then the pairs of corresponding angles are congruent. 1 2 Because of the corresponding angles postulate

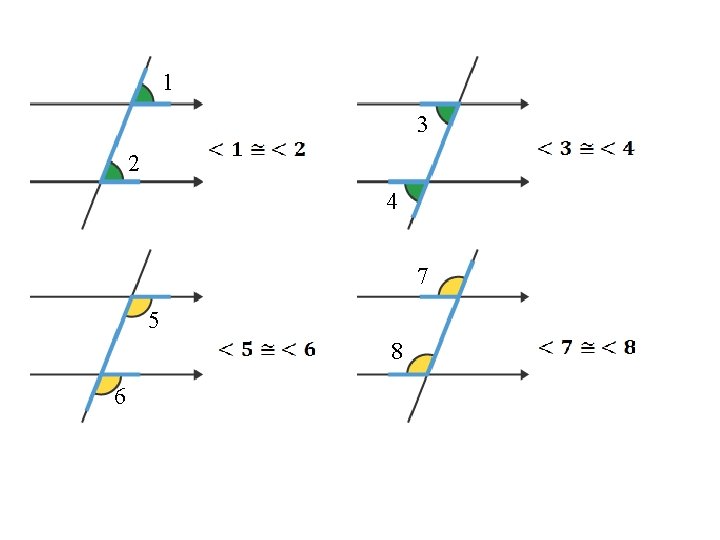
1 3 2 4 7 5 8 6

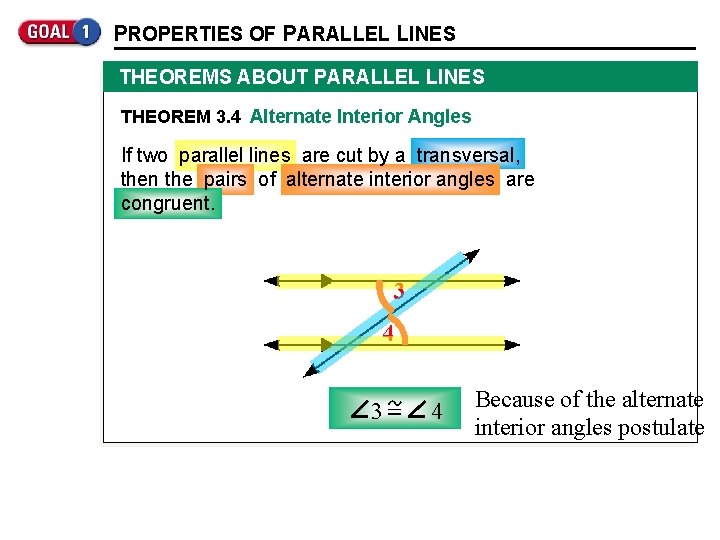
PROPERTIES OF PARALLEL LINES THEOREMS ABOUT PARALLEL LINES THEOREM 3. 4 Alternate Interior Angles If two parallel lines are cut by a transversal, then the pairs of alternate interior angles are congruent. 3 4 Because of the alternate interior angles postulate

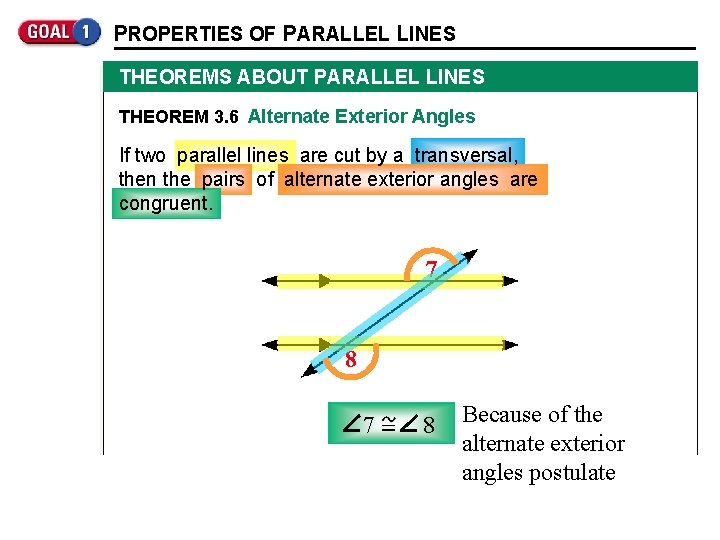
PROPERTIES OF PARALLEL LINES THEOREMS ABOUT PARALLEL LINES THEOREM 3. 6 Alternate Exterior Angles If two parallel lines are cut by a transversal, then the pairs of alternate exterior angles are congruent. 7 8 Because of the alternate exterior angles postulate

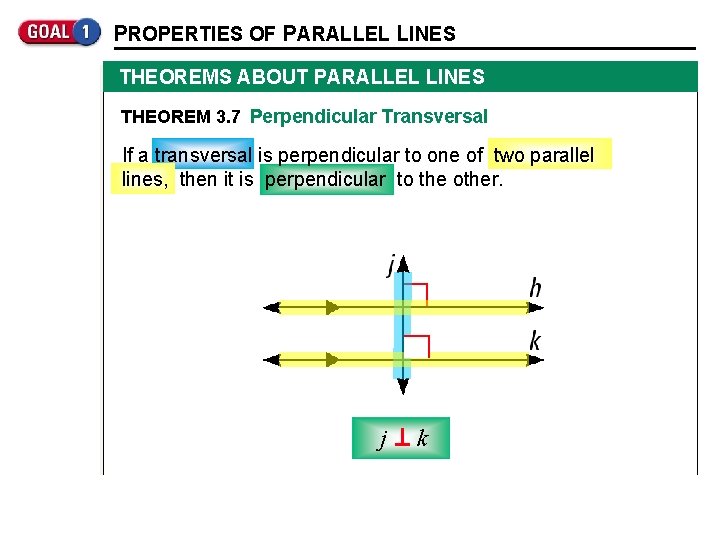
PROPERTIES OF PARALLEL LINES THEOREMS ABOUT PARALLEL LINES THEOREM 3. 7 Perpendicular Transversal If a transversal is perpendicular to one of two parallel lines, then it is perpendicular to the other. j k

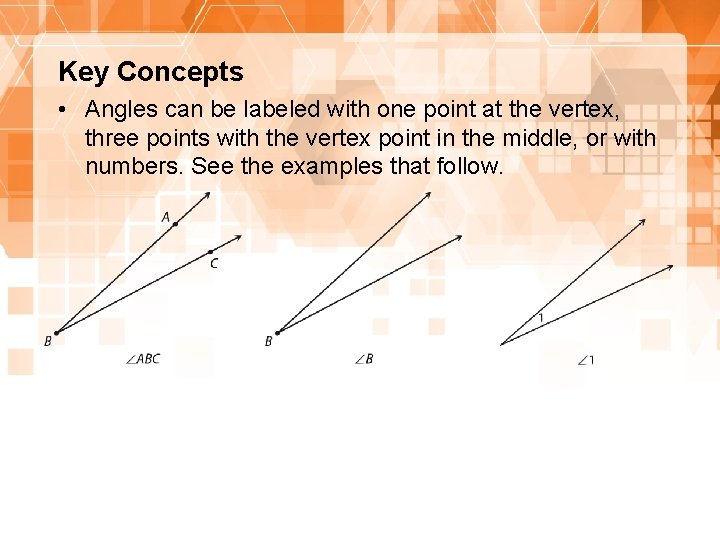
Key Concepts • Angles can be labeled with one point at the vertex, three points with the vertex point in the middle, or with numbers. See the examples that follow. 14 1. 8. 1: Proving the Vertical Angles Theorem

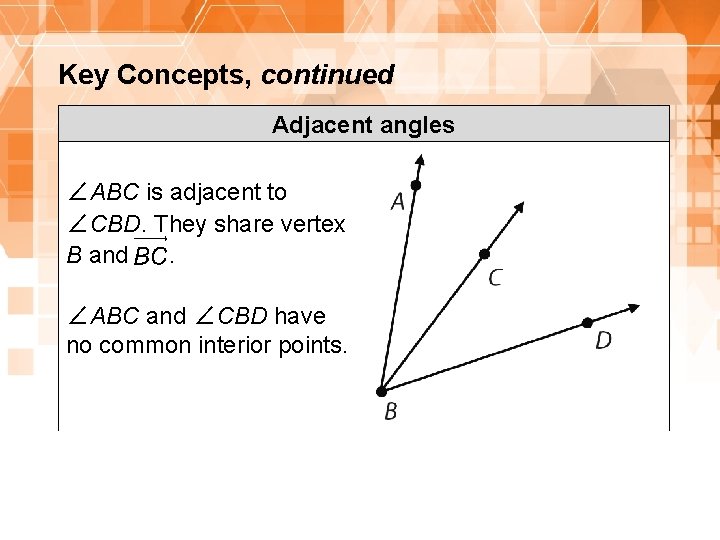
Key Concepts, continued Adjacent angles ∠ABC is adjacent to ∠CBD. They share vertex B and. ∠ABC and ∠CBD have no common interior points. 15 1. 8. 1: Proving the Vertical Angles Theorem

Key Concepts, continued Nonadjacent angles ∠ABE is not adjacent to ∠FCD. They do not have a common vertex. (continued) 16 1. 8. 1: Proving the Vertical Angles Theorem

Key Concepts, continued Nonadjacent angles ∠PQS is not adjacent to ∠PQR. They share common interior points within ∠PQS. 17 1. 8. 1: Proving the Vertical Angles Theorem

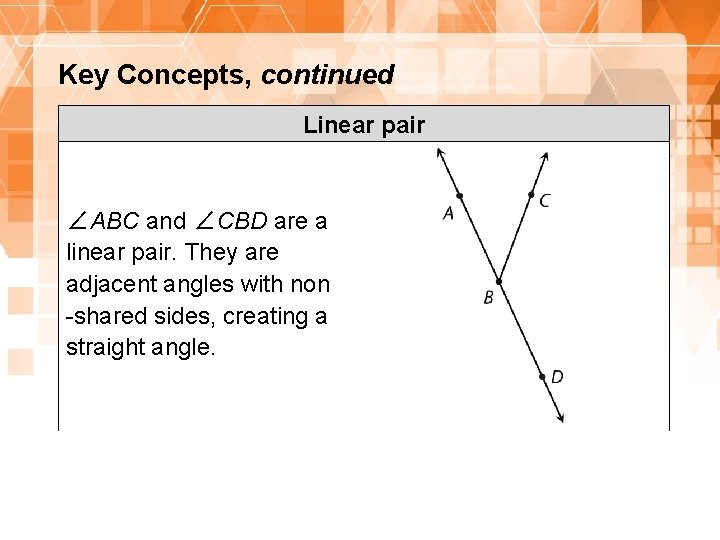
Key Concepts, continued Linear pair ∠ABC and ∠CBD are a linear pair. They are adjacent angles with non -shared sides, creating a straight angle. 18 1. 8. 1: Proving the Vertical Angles Theorem

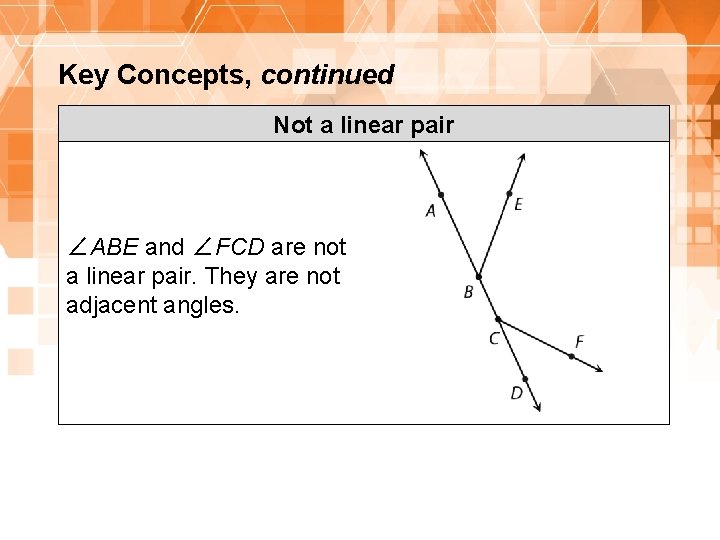
Key Concepts, continued Not a linear pair ∠ABE and ∠FCD are not a linear pair. They are not adjacent angles. 19 1. 8. 1: Proving the Vertical Angles Theorem

Vertical angles are nonadjacent angles formed by two pairs of opposite rays. Opposite angles are congruent to each other. 20 1. 8. 1: Proving the Vertical Angles Theorem

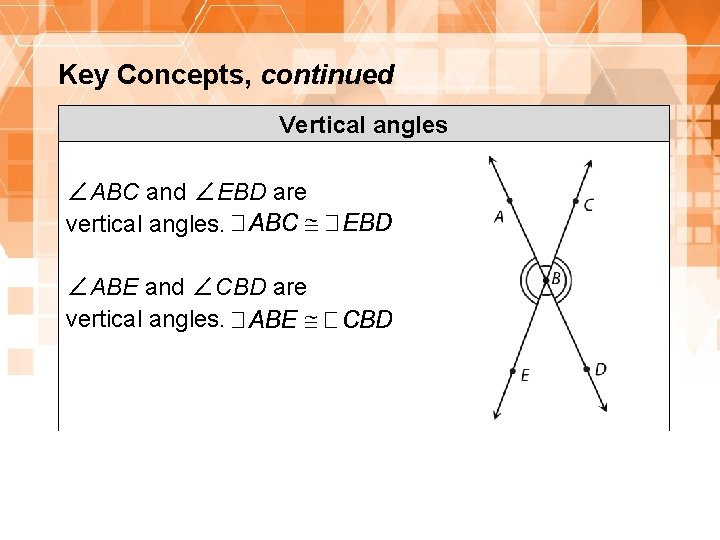
Key Concepts, continued Vertical angles ∠ABC and ∠EBD are vertical angles. ∠ABE and ∠CBD are vertical angles. 21 1. 8. 1: Proving the Vertical Angles Theorem

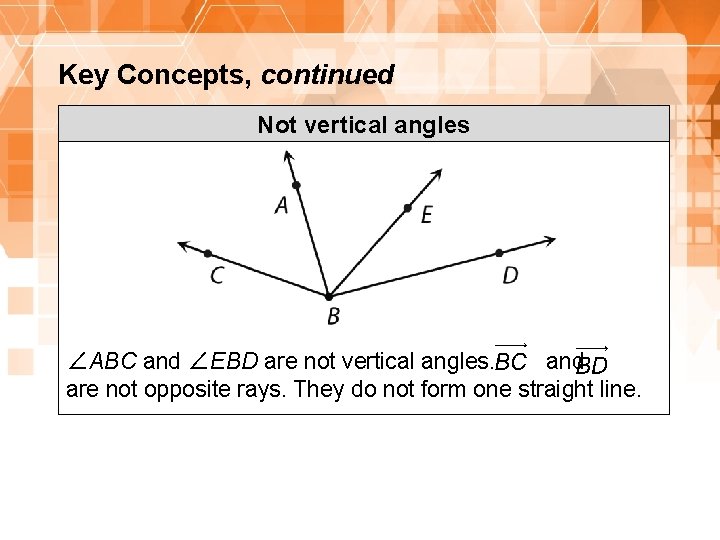
Key Concepts, continued Not vertical angles ∠ABC and ∠EBD are not vertical angles. and are not opposite rays. They do not form one straight line. 22 1. 8. 1: Proving the Vertical Angles Theorem

Key Concepts, continued Theorem Supplementary Theorem If two angles add up to be 180 degrees, then they are supplementary. 23 1. 8. 1: Proving the Vertical Angles Theorem

Key Concepts, continued • Complementary angles are two angles whose sum is 90º. Complementary angles can form a right angle or be nonadjacent. 24 1. 8. 1: Proving the Vertical Angles Theorem