Lesson 29 Trigonometric Functions Pre Calculus Santowski 1162022


















- Slides: 22

Lesson 29 – Trigonometric Functions Pre. Calculus - Santowski 1/16/2022 Pre. Calculus - Santowski 1

Lesson Objectives n Make the connection between angles in standard position and sinusoidal functions n Graph and analyze a periodic function n Introduce transformations of periodic functions 1/16/2022 Pre. Calculus - Santowski 2

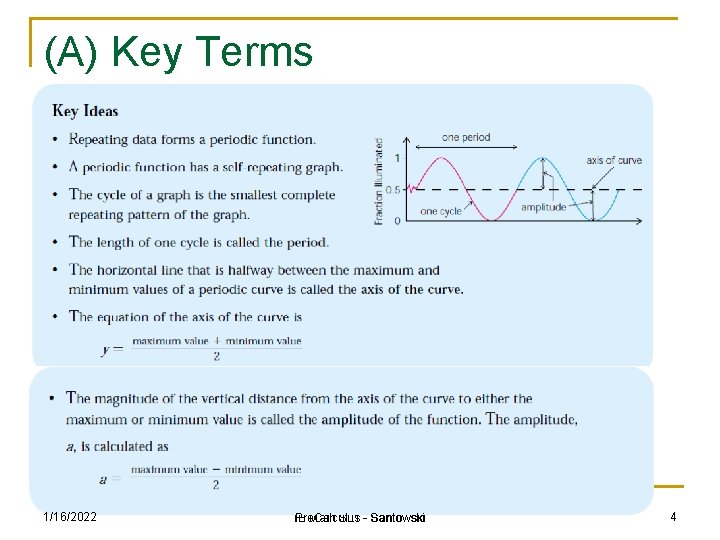
(A) Key Terms Related to Periodic Functions n Define the following key terms that relate to trigonometric functions: n (a) period (b) amplitude (c) axis of the curve (or equilibrium axis) (d) domain (e) range (f) roots (g) maximum/minimum n n n 1/16/2022 IB Pre. Calculus Math SL 1 - Santowski 3

(A) Key Terms 1/16/2022 IB Pre. Calculus Math SL 1 - Santowski 4

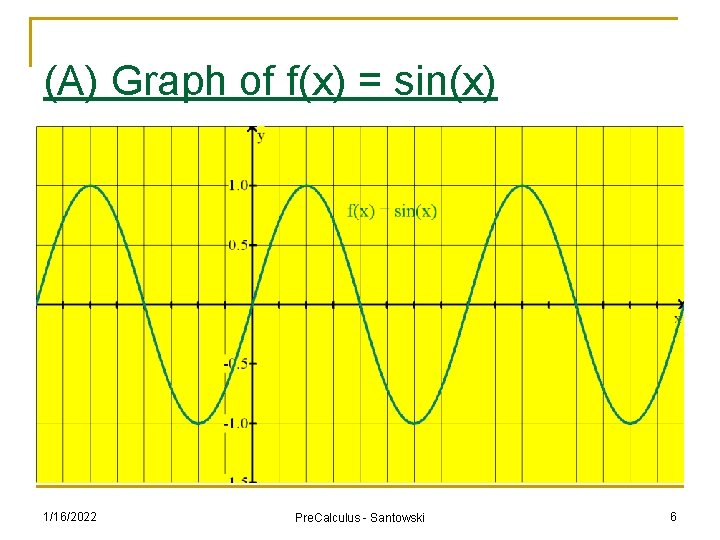
(A) Graph of f(x) = sin(x) n We can use our knowledge of angles on Cartesian plane and our knowledge of the trig ratios of special angles to create a list of points to generate a graph of f(x) = sin(x) n See link at http: //www. univie. ac. at/future. media/moe/galerie/fun 2. html#sincostan 1/16/2022 Pre. Calculus - Santowski 5

(A) Graph of f(x) = sin(x) 1/16/2022 Pre. Calculus - Santowski 6

(A) Features of f(x) = sin(x) n n n n n The graph is periodic (meaning that it repeats itself) Domain: Range: Period: length of one cycle, how long does the pattern take before it repeats itself . x-intercepts: Axis of the curve or equilibrium axis: amplitude: max height above equilibrium position - how high or low do you get y-intercept: max. points: min. points: 1/16/2022 Pre. Calculus - Santowski 7

(A) Features of f(x) = sin(x) n n n n n The graph is periodic (meaning that it repeats itself) Domain: x E R Range: [-1, 1] Period: length of one cycle, how long does the pattern take before it repeats itself 360° or 2 π rad. x-intercepts: every 180°, x = 180°n where n E I or πn where n E I. Axis of the curve or equilibrium axis: x-axis amplitude: max height above equilibrium position - how high or low do you get => 1 unit y-intercept: (0°, 0) max. points: 90°+ 360°n (or 2π + 2 π n) min. points: 270°+ 360°n or -90° + 360°n or -π/2 + 2 π n 1/16/2022 Pre. Calculus - Santowski 8

(A) Features of f(x) = sin(x) n Five point summary of f(x) = sin(x) x y=f(x) 1/16/2022 Pre. Calculus - Santowski 9

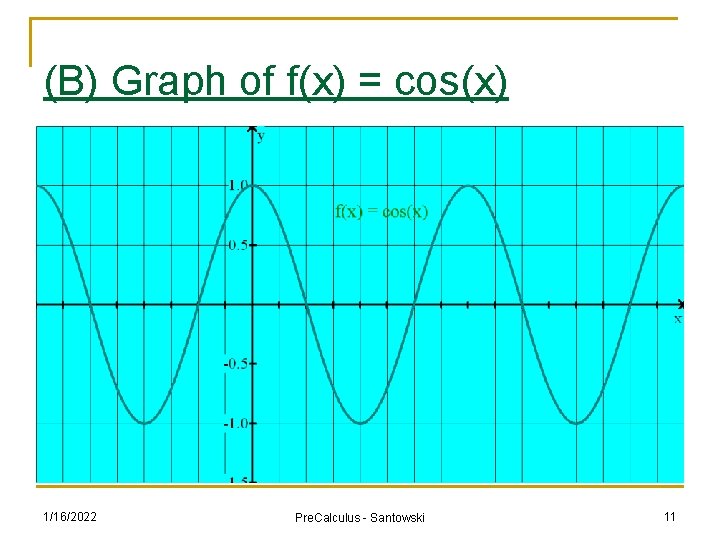
(B) Graph of f(x) = cos(x) n We can use our knowledge of angles on Cartesian plane and our knowledge of the trig ratios of special angles to create a list of points to generate a graph of f(x) = cos(x) n See link at http: //www. univie. ac. at/future. media/moe/galerie/fun 2. html#sincostan 1/16/2022 Pre. Calculus - Santowski 10

(B) Graph of f(x) = cos(x) 1/16/2022 Pre. Calculus - Santowski 11

(B) Features of f(x) = cos(x) n n n n n The graph is periodic Domain: Range: Period: length of one cycle, how long does the pattern take before it repeats itself . x-intercepts: Axis of the curve or equilibrium axis: amplitude: max height above equilibrium position - how high or low do you get y-intercept: max. points: min. points: 1/16/2022 Pre. Calculus - Santowski 12

(B) Features of f(x) = cos(x) n n n n n The graph is periodic Domain: x E R Range: [-1, 1] Period: length of one cycle, how long does the pattern take before it repeats itself 360° or 2 π rad. x-intercepts: every 180° starting at 90°, x = 90° + 180°n where n E I (or π/2 + π n where n E I) Axis of the curve or equilibrium axis: x-axis amplitude: max height above equilibrium position - how high or low do you get => 1 unit y-intercept: (0°, 1) max. points: 0° + 360°n ( 2 π n) min. points: 180° + 360°n or -180° + 360°n (or π + 2 π n) 1/16/2022 Pre. Calculus - Santowski 13

(B) Features of f(x) = cos(x) n Five point summary of f(x) = cos(x) x y=f(x) 1/16/2022 Pre. Calculus - Santowski 14

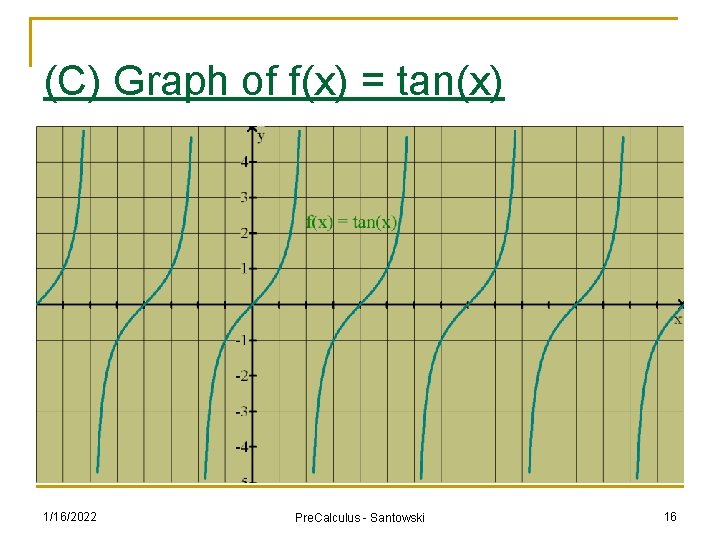
(C) Graph of f(x) = tan(x) n We can use our knowledge of angles on Cartesian plane and our knowledge of the trig ratios of special angles to create a list of points to generate a graph of f(x) = tan(x) n See link at http: //www. univie. ac. at/future. media/moe/galerie/fun 2. html#sincostan 1/16/2022 Pre. Calculus - Santowski 15

(C) Graph of f(x) = tan(x) 1/16/2022 Pre. Calculus - Santowski 16

(C) Features of f(x) = tan(x) n n n n n The graph is periodic Domain: Asymptotes: Range: Period: length of one cycle, how long does the pattern take before it repeats itself x-intercepts: amplitude: max height above equilibrium position - how high or low do you get y-intercept: max. points: min. points: 1/16/2022 Pre. Calculus - Santowski 17

(C) Features of f(x) = tan(x) n n n n n The graph is periodic Domain: x E R where x cannot equal 90°, 270°, 450°, or basically 90° + 180°n where n E I Asymptotes: every 180° starting at 90° Range: x E R Period: length of one cycle, how long does the pattern take before it repeats itself = 180° or π rad. x-intercepts: x = 0°, 180°, 360°, or basically 180°n where n E I or x = πn amplitude: max height above equilibrium position - how high or low do you get => none as it stretches on infinitely y-intercept: (0°, 0) max. points: none min. points: none 1/16/2022 Pre. Calculus - Santowski 18

(C) Features of f(x) = tan(x) n Five point summary of f(x) = tan(x) x y=f(x) 1/16/2022 Pre. Calculus - Santowski 19

Graphs of Secondary Trig Fcns csc n Recall that csc(x) = 1/sin(x) n Here is a data table for y = sin(x) x 0 30 60 90 120 150 180 210 240 270 300 330 360 y 0 0. 5 0. 87 1 0. 87 0. 5 0 -0. 5 -0. 87 -1 -0. 87 -0. 5 0 n How would you prepare a graph for y = csc(x)? 1/16/2022 Pre. Calculus - Santowski 20

Graphs of Secondary Trig Fcns sec n Recall that sec(x) = 1/cos(x) n Here is a data table for y = cos(x) x 0 30 60 90 120 150 180 210 240 270 300 330 360 y 1 0. 87 0. 5 0 -0. 5 -0. 87 -1 -0. 87 -0. 5 0. 87 1 n How would you prepare a graph for y = sec(x)? 1/16/2022 Pre. Calculus - Santowski 21

Graphs of Secondary Trig Fcns cot n Recall that cot(x) = 1/tan(x) n Here is a data table for y = tan(x) x 0 30 60 90 120 150 180 210 240 270 300 330 360 y 0 0. 57 1. 73 Und. -1. 73 -0. 57 0 n How would you prepare a graph for y = cot(x)? 1/16/2022 Pre. Calculus - Santowski 22
 Honors precalculus chapter 1 test
Honors precalculus chapter 1 test Pre ap calculus quiz 1
Pre ap calculus quiz 1 Pre calculus unit 1 review
Pre calculus unit 1 review Znacznik pre /pre jest stosowany w celu wyświetlenia
Znacznik pre /pre jest stosowany w celu wyświetlenia Pre ap precalculus
Pre ap precalculus Calculus
Calculus Mathematics functions grade 12
Mathematics functions grade 12 6 trig functions
6 trig functions Three basic trigonometric functions
Three basic trigonometric functions Partner of sine and cosine
Partner of sine and cosine How to find period in sine function
How to find period in sine function 12-7 graphing trigonometric functions answers
12-7 graphing trigonometric functions answers 12-1 trigonometric functions in right triangles
12-1 trigonometric functions in right triangles Differentiate trigonometric
Differentiate trigonometric Graphing sine and cosine functions quiz
Graphing sine and cosine functions quiz Domain and range of trigonometric functions
Domain and range of trigonometric functions Limit of trigonometric functions
Limit of trigonometric functions 4-6 practice inverse trigonometric functions answer key
4-6 practice inverse trigonometric functions answer key 4-5 practice graphing other trigonometric functions
4-5 practice graphing other trigonometric functions Parts of trigonometric functions
Parts of trigonometric functions Trigonometry range and domain
Trigonometry range and domain Derivative of secx
Derivative of secx Period of trigonometric functions
Period of trigonometric functions