Lesson 28 TRIANGLE CONGRUENCE SIDEANGLESIDE SAS New Vocabulary

Lesson 28 TRIANGLE CONGRUENCE: SIDE-ANGLE-SIDE SAS

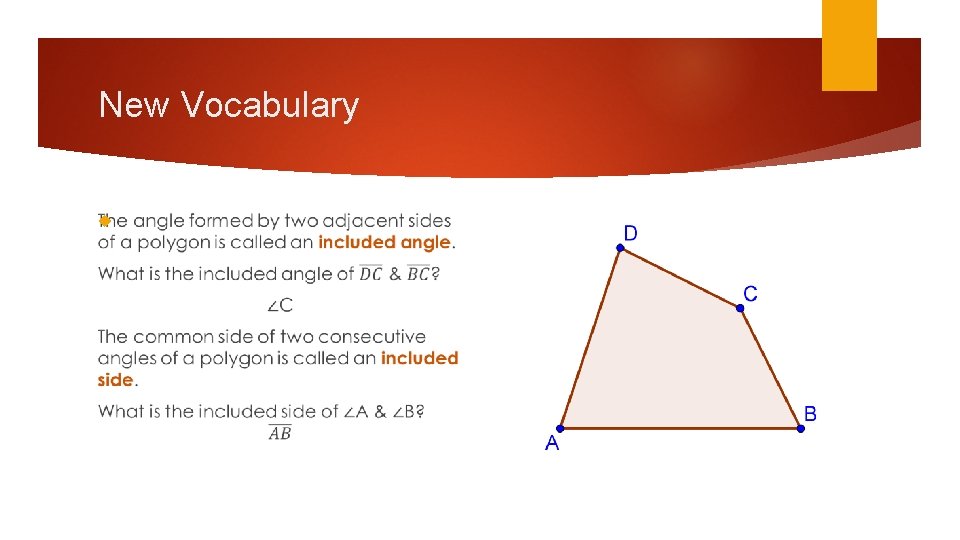
New Vocabulary

Postulate 15: Side-Angle-Side (SAS) Triangle Congruence Postulate If 2 sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle, then the triangles are congruent. ΔACD ≅ ΔFEB, SAS The triangle congruence statement must be written in corresponding order. For example ΔACD is not ≅ ΔBEF

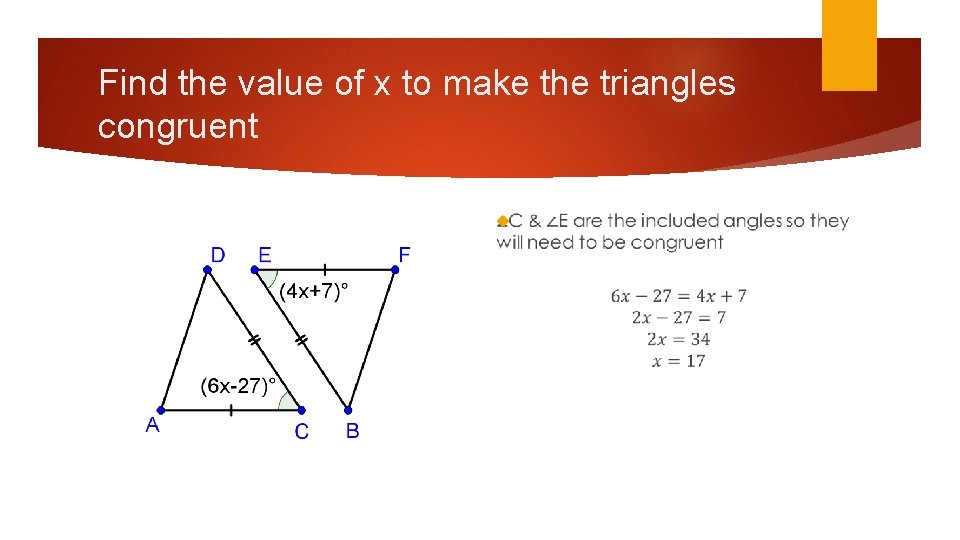
Find the value of x to make the triangles congruent

You have a pond and you need to estimate its length. However, you have no way to measure it directly You can create congruent triangles on the land surrounding the pond like so

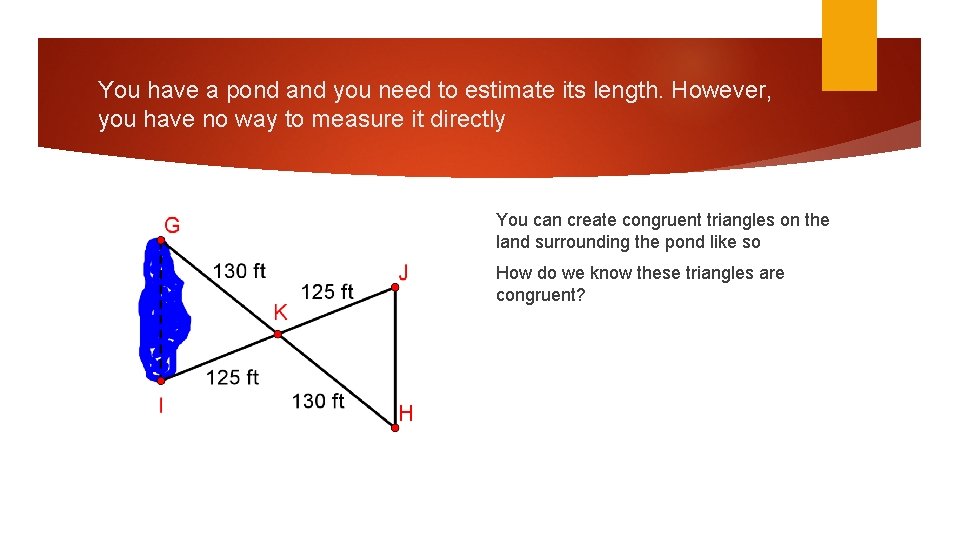
You have a pond and you need to estimate its length. However, you have no way to measure it directly You can create congruent triangles on the land surrounding the pond like so How do we know these triangles are congruent?

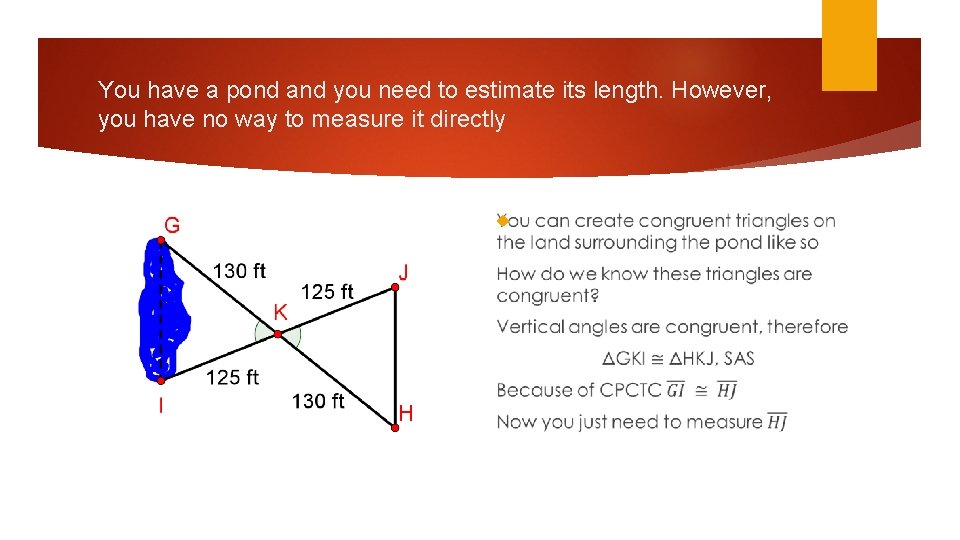
You have a pond and you need to estimate its length. However, you have no way to measure it directly

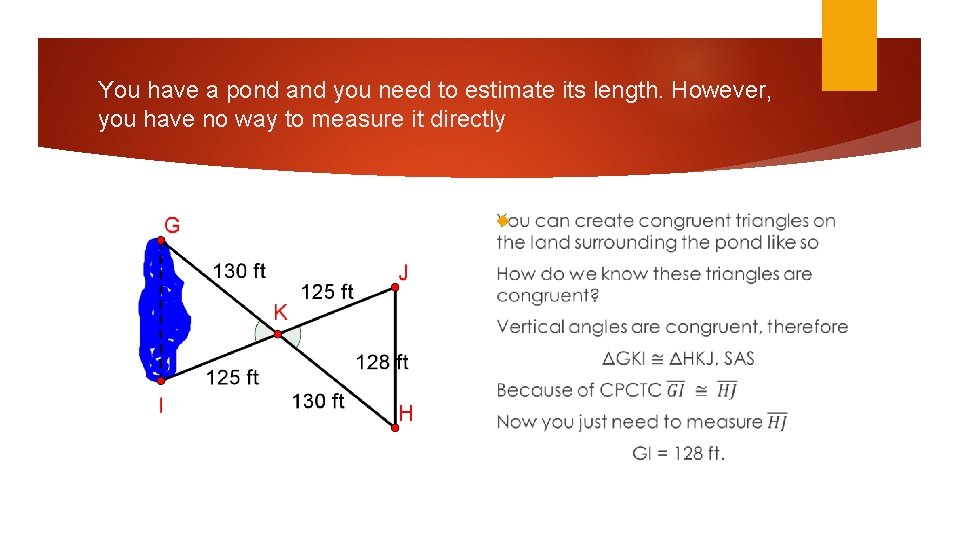
You have a pond and you need to estimate its length. However, you have no way to measure it directly

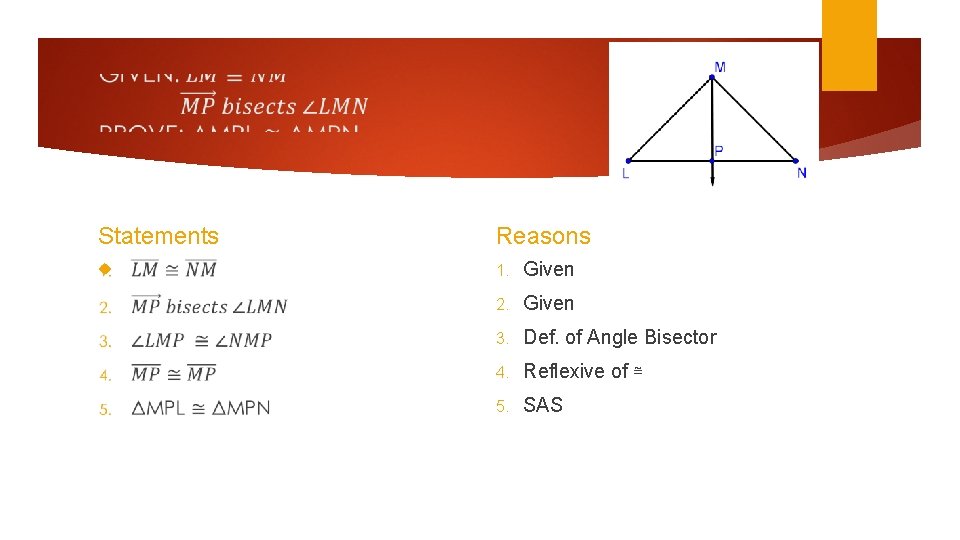
Statements Reasons 1. Given 2. Given 3. Def. of Angle Bisector 4. Reflexive of ≅ 5. SAS

Statements Reasons 1. Given 2. Thm 5 -4 (┴ lines, form ≅ ∠’s) 3. Def. of Segment Bisector 4. Reflexive of ≅ 5. SAS

Conclusion Proving triangles congruent and identifying included sides and included angles will prepare us for more triangle congruence like: ASA & AAS HL, LA, HA We will also need these skills when finding similar triangles and other polygons