LESSON 24 INFERENCES USING REGRESSION Outline AssumptionsPitfalls in

LESSON 24: INFERENCES USING REGRESSION Outline • Assumptions/Pitfalls in Regression Analysis • Coefficient of Determination/Correlation Coefficient • Inferences using the Regression Line 1

LINEAR REGRESSION ASSUMPTIONS • The conditional means all lie on the same straight line and the sample observations • All populations have the same standard deviation • Successive sample observations are independent • The value of is known in advance 2

LINEAR REGRESSION ASSUMPTIONS • The true regression coefficients and are usually unknown and are estimated from the sample counterparts • For multiple regression, the true regression plane • and each sample observation 3

PITFALLS IN MULTIPLE REGRESSION • Multicollinearity – High correlation between two independent variables – Solution: eliminate one of the two variables that are correlated 4

COEFFICIENT OF DETERMINATION • Total sum of squares / Total variation • Regression sum of squares / Explained variation • Error sum of squares / Unexplained variation 5

COEFFICIENT OF DETERMINATION • Coefficient of determination 6

INFERENCES USING REGRESSION LINE • Confidence interval for the conditional mean using small samples 7

INFERENCES USING REGRESSION LINE • Prediction interval for an individual Y using small samples 8

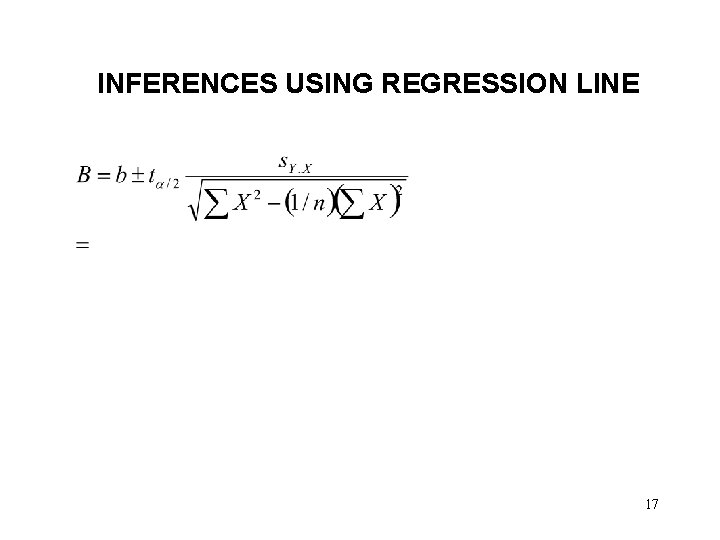
INFERENCES USING REGRESSION LINE • Confidence interval estimate of the true slope B 9

INFERENCES USING REGRESSION LINE • Hypotheses Test regarding B: A testing procedure will find whether or not two variables are correlated, and if so whether the slope is positive or negative • Hypotheses: • Test Statistics: d. f. =n - 2 10

INFERENCES USING REGRESSION LINE • Confidence interval estimate of the true intercept A 11

INFERENCES USING REGRESSION LINE Example 1: Refer to Lesson 20, Example 1 (rewritten below). Construct a 98% confidence interval estimate of the conditional mean final product weight when the raw-materials volume is 25 gallons. Recall that Y = weight of final product in pounds and X = volume of raw materials in gallons. X 14 23 9 17 10 Y 68 105 40 79 51 12

INFERENCES USING REGRESSION LINE 13

INFERENCES USING REGRESSION LINE Example 2: Refer to Example 1 (rewritten below). Construct a 98% prediction interval estimate of the final product weight in an individual batch having 20 gallons of raw materials. Recall that Y = weight of final product in pounds and X = volume of raw materials in gallons. X 14 23 9 17 10 Y 68 105 40 79 51 14

INFERENCES USING REGRESSION LINE 15

INFERENCES USING REGRESSION LINE Example 3: Refer to Example 1. a. Construct a 95% confidence interval estimate of the slope of the true regression line. b. At the 5% significance level, must you accept or reject the null hypothesis that final product weight (Y) and raw materials volume (X) are uncorrelated variables? X Y 14 68 23 105 9 40 17 79 16 10 51

INFERENCES USING REGRESSION LINE 17

READING AND EXERCISES Lesson 24 Reading: Section 12 -1 to 12 -3 pp. 412 -433 Exercises: 12 -11, 12 -13, 12 -19 18