Lesson 23 Secondary Trigonometric Functions Inverse Trig Functions

Lesson 23 – Secondary Trigonometric Functions & Inverse Trig Functions IB Math HL 1/21/2022 Math HL 1

Lesson Objectives n 1. Relate the features of sinusoidal curves to modeling periodic phenomenon n 2. Transformations of sinusoidal functions and their features 1/21/2022 Math HL 2

Working with Graphs of the Secondary Trig Functions n (a) Sketch 2 cycles of the graph of y = sin(x) n (b) Hence, sketch y = csc(x) & label key features (asymptotes, max/min, x- & y-int) n (c) Hence, sketch 2 cycles of y = 2 csc(2 x) – 4 and label key features (asymptotes, max/min, x- & y-int. 1/21/2022 Math HL 3

Working with Graphs of the Secondary Trig Functions n (a) Sketch a graph of two periods of f(x) = 2 + cos(x) n (b) Sketch a graph of two periods of g(x) = -sec(x) n (c) How many solutions would you predict for the system f(x) = g(x)? Find the exact values of these solutions 1/21/2022 Math HL 4

Advanced Sinusoidals n Predict the domains of the following composite functions 1/21/2022 Math HL 5

Review of Inverse Functions n Q What is the significance of a function being 1: 1 in the context of inverse functions? n Q Is f(x) = x 2 a 1: 1 function? n Q How did we “resolve” this issue with the function f(x) = x 2? 1/21/2022 Precalculus - Santowski 6

Restricted Domains n (a) How would you restrict the domain of g(x) = sin(x) so that its inverse is a function? Use your calculator to justify your choice. (numerically & graphically) n (b) How would you restrict the domain of g(x) = cos(x) so that its inverse is a function? Use your calculator to justify your choice. (numerically & graphically) n (c) How would you restrict the domain of g(x) = tan(x) so that its inverse is a function? Use your calculator to justify your choice. (numerically & graphically) 1/21/2022 Precalculus - Santowski 7

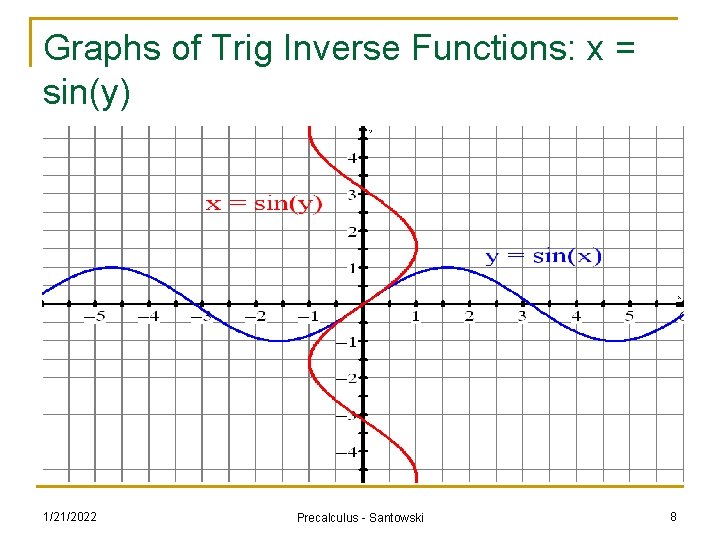
Graphs of Trig Inverse Functions: x = sin(y) 1/21/2022 Precalculus - Santowski 8

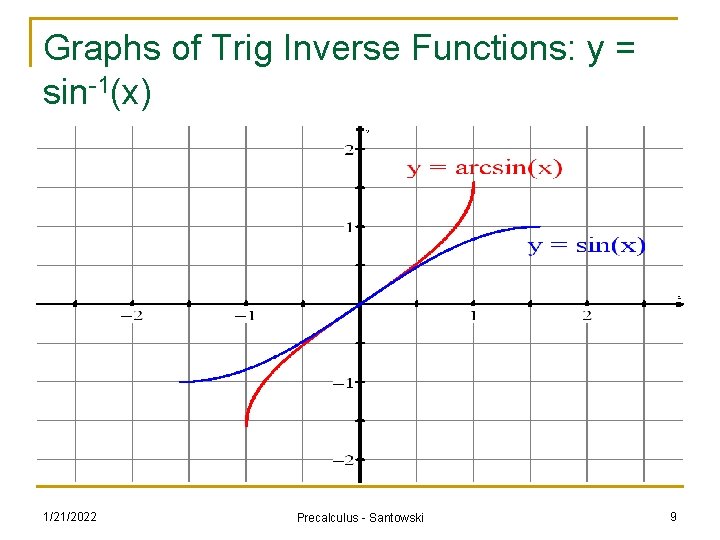
Graphs of Trig Inverse Functions: y = sin-1(x) 1/21/2022 Precalculus - Santowski 9

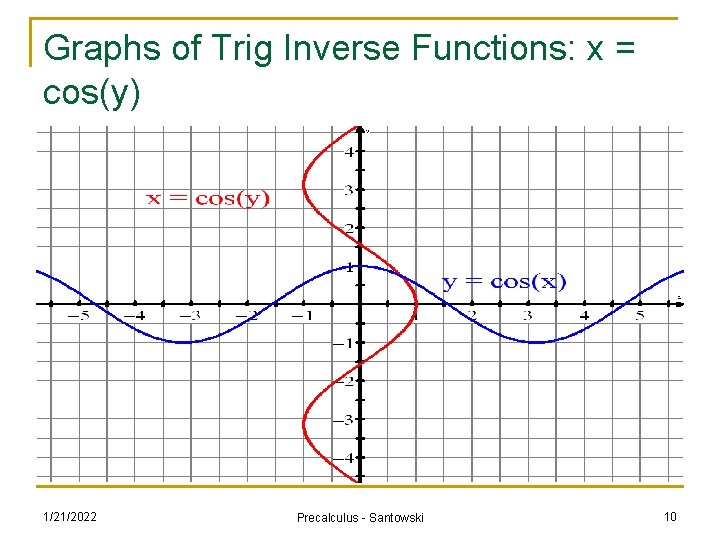
Graphs of Trig Inverse Functions: x = cos(y) 1/21/2022 Precalculus - Santowski 10

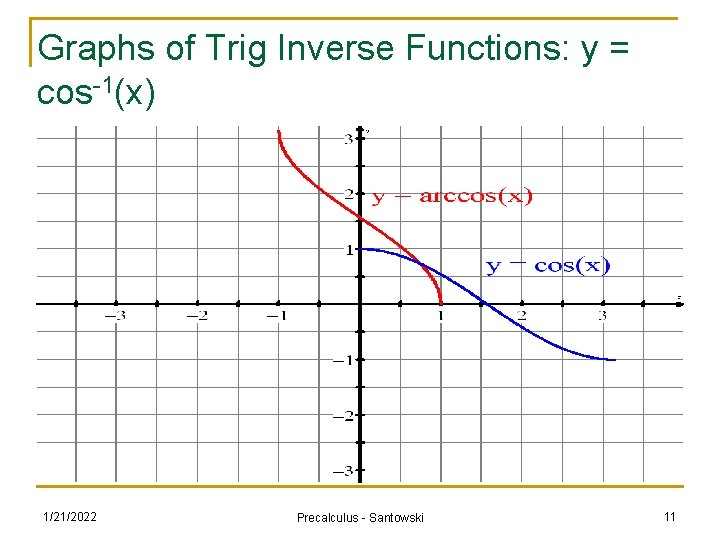
Graphs of Trig Inverse Functions: y = cos-1(x) 1/21/2022 Precalculus - Santowski 11

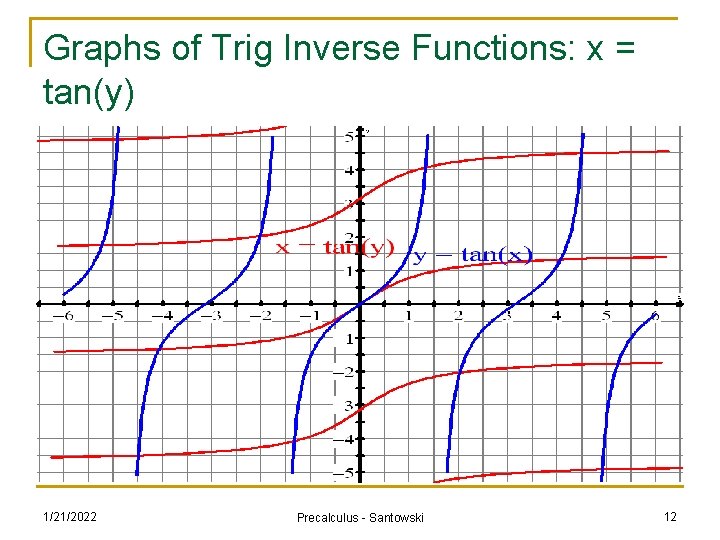
Graphs of Trig Inverse Functions: x = tan(y) 1/21/2022 Precalculus - Santowski 12

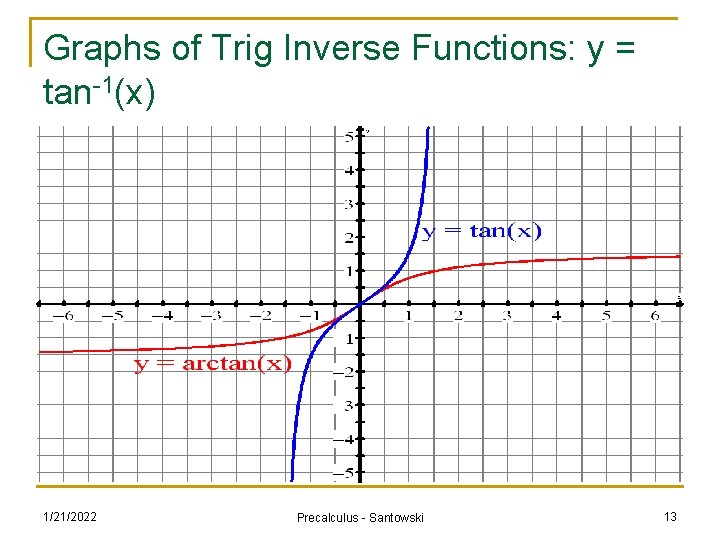
Graphs of Trig Inverse Functions: y = tan-1(x) 1/21/2022 Precalculus - Santowski 13