Lesson 2 Motion with Constant Acceleration Position with

Position with Constant Acceleration • The graph shows that the car’s motion is not

Position with Constant Acceleration • The slopes from the position time graph can be

Velocity vs. Time Graphs • Slope of velocity time graph is acceleration • If

Distance Traveled The area under a velocity time graph gives you the distance traveled

Average and Instantaneous Acceleration • The average acceleration of an object is the change

Average and Instantaneous Acceleration • A curved line on a velocity-time graph shows that

Velocity with Average Acceleration • If an object’s average acceleration during a time interval

Velocity with Average Acceleration • In cases in which the acceleration is constant, the

Velocity with Average Acceleration Response Use with Example Problem 3. Problem The v-t graph

Slides: 12

Download presentation

Lesson 2 Motion with Constant Acceleration

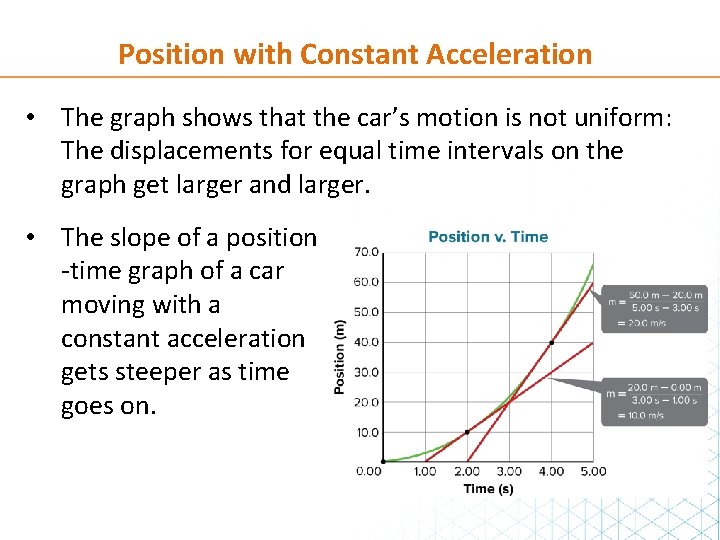
Position with Constant Acceleration • The graph shows that the car’s motion is not uniform: The displacements for equal time intervals on the graph get larger and larger. • The slope of a position -time graph of a car moving with a constant acceleration gets steeper as time goes on.

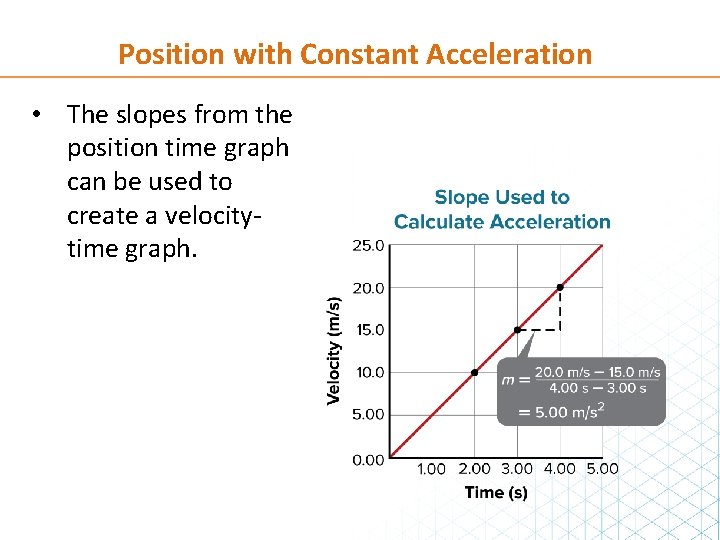
Position with Constant Acceleration • The slopes from the position time graph can be used to create a velocitytime graph.

Velocity vs. Time Graphs • Slope of velocity time graph is acceleration • If line is curved, can find the instantaneous acceleration by finding the slope of a tangent to the curve at that point

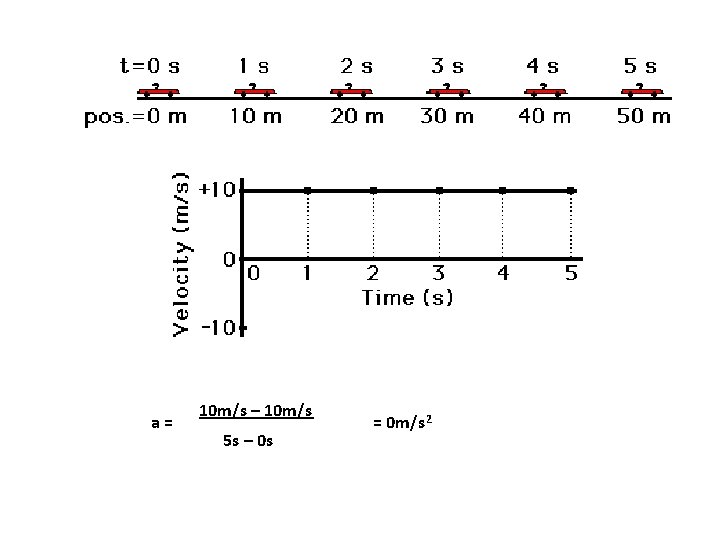
a= 10 m/s – 10 m/s 5 s – 0 s = 0 m/s 2

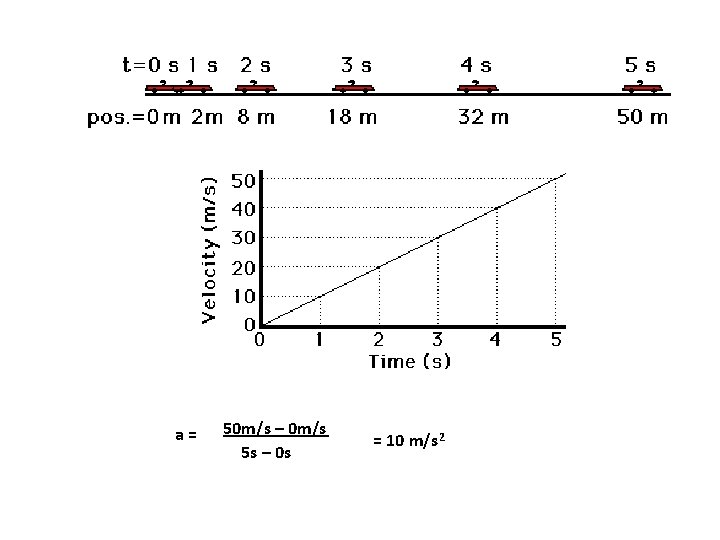
a= 50 m/s – 0 m/s 5 s – 0 s = 10 m/s 2

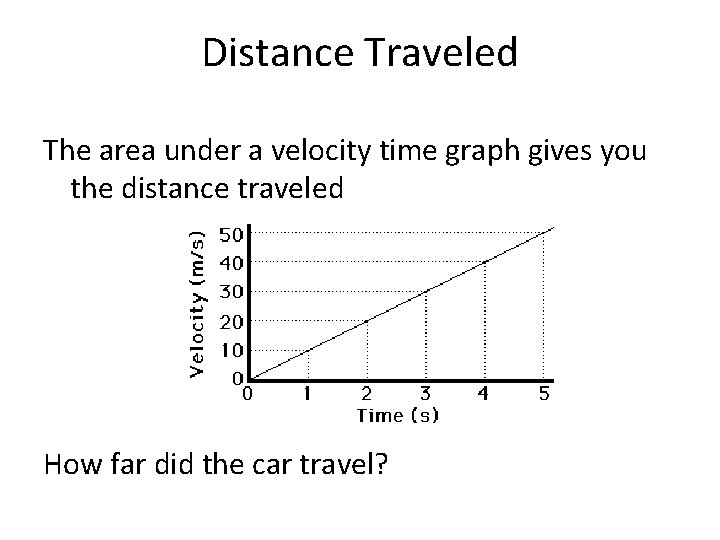
Distance Traveled The area under a velocity time graph gives you the distance traveled How far did the car travel?

Average and Instantaneous Acceleration • The average acceleration of an object is the change in velocity during some measurable time interval divided by that time interval. • The change in velocity at an instant of time is called instantaneous acceleration. • The instantaneous acceleration of an object can be found by drawing a tangent line on the velocity-time graph at the point of time in which you are interested. • The slope of this line is equal to the instantaneous acceleration.

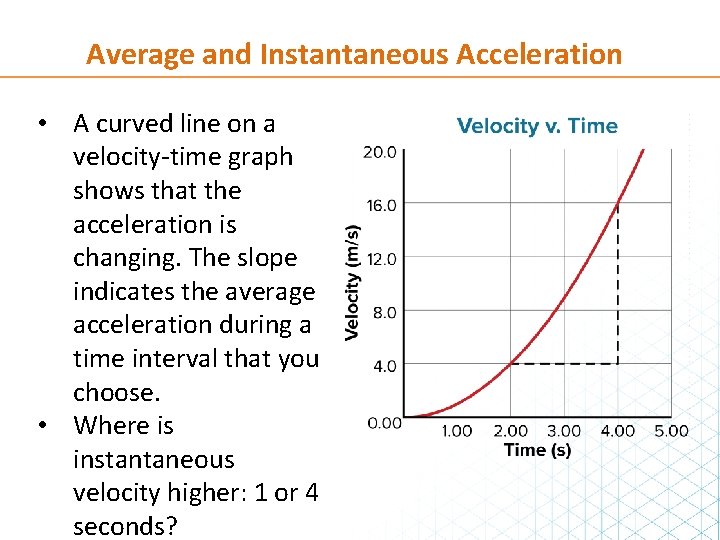
Average and Instantaneous Acceleration • A curved line on a velocity-time graph shows that the acceleration is changing. The slope indicates the average acceleration during a time interval that you choose. • Where is instantaneous velocity higher: 1 or 4 seconds?

Velocity with Average Acceleration • If an object’s average acceleration during a time interval is known, then it can be used to determine how much the velocity changed during that time. Final Velocity with Average Acceleration • The final velocity is equal to the initial velocity plus the product of the average acceleration and the time interval.

Velocity with Average Acceleration • In cases in which the acceleration is constant, the average acceleration (ā) is the same as the instantaneous acceleration (a). • The equation for final velocity can be rewritten to find the time at which an object with constant acceleration has a given velocity. • It also can be used to calculate the initial velocity of an object when both the velocity and the time at which it occurred are given.

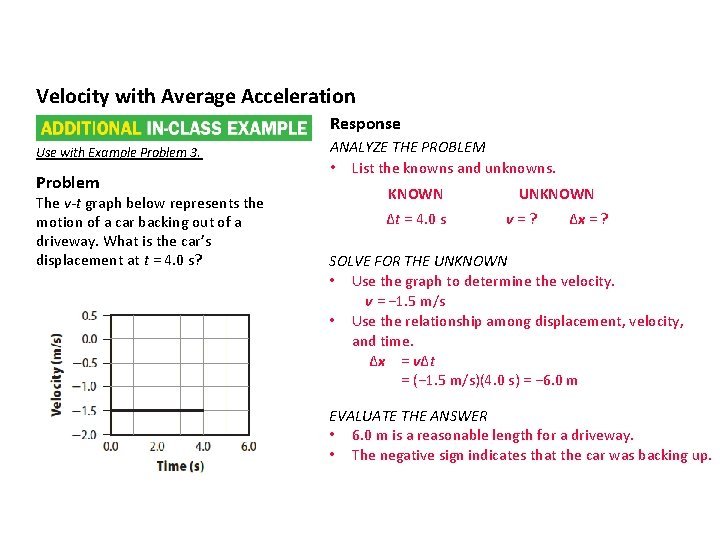
Velocity with Average Acceleration Response Use with Example Problem 3. Problem The v-t graph below represents the motion of a car backing out of a driveway. What is the car’s displacement at t = 4. 0 s? ANALYZE THE PROBLEM • List the knowns and unknowns. KNOWN Δt = 4. 0 s UNKNOWN v=? Δx = ? SOLVE FOR THE UNKNOWN • Use the graph to determine the velocity. v = − 1. 5 m/s • Use the relationship among displacement, velocity, and time. Δx = vΔt = (− 1. 5 m/s)(4. 0 s) = − 6. 0 m EVALUATE THE ANSWER • 6. 0 m is a reasonable length for a driveway. • The negative sign indicates that the car was backing up.