Lesson 2 8 Core Focus on Linear Equations

Lesson 2. 8 Core Focus on Linear Equations The Slope Formula

Warm-Up Draw a line through each pair of points. Draw a slope triangle and find the slope. 1. (1, 3) and (5, 4) 2. (− 2, 6) and (1, 0) − 2

Lesson 2. 8 The Slope Formula Find the slope of a line using the slope formula.

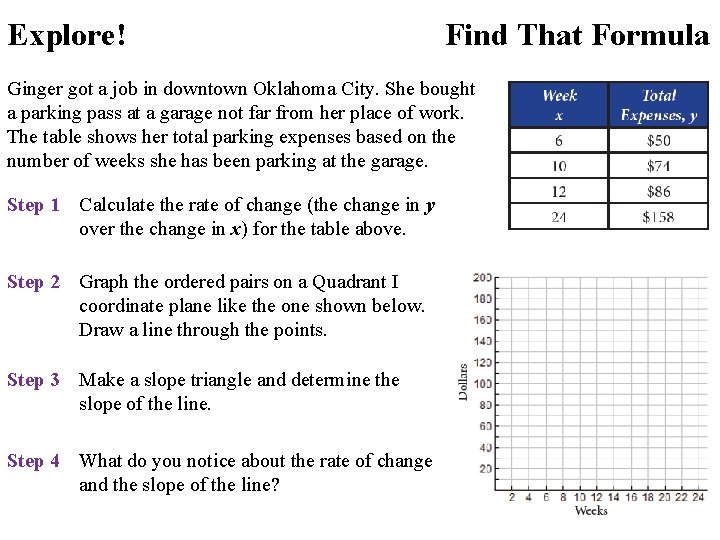
Explore! Find That Formula Ginger got a job in downtown Oklahoma City. She bought a parking pass at a garage not far from her place of work. The table shows her total parking expenses based on the number of weeks she has been parking at the garage. Step 1 Calculate the rate of change (the change in y over the change in x) for the table above. Step 2 Graph the ordered pairs on a Quadrant I coordinate plane like the one shown below. Draw a line through the points. Step 3 Make a slope triangle and determine the slope of the line. Step 4 What do you notice about the rate of change and the slope of the line?

Explore! Multi-Step Equation Step 5 If you were given the table of values in the table to the right, what would the rate of change (or slope) ratio look like? Step 6 The ratio developed in Step 5 is called the “Slope Formula”. The subscripts identify two different points. Try your formula on these points from the table above: (6, 50) and (12, 86). Did you get the same slope as you did in Steps 1 and 3? Step 7 You have learned three methods for finding slope: rate of change, slope triangles and the slope formula. Which method do you like the best? Why?

The Slope Formula The formula for the slope of a line that goes through a point with coordinates (x 1, y 1) and another point with coordinates (x 2, y 2) is: You read x 1 as “x sub one. ” Think of it as saying “the x-coordinate of the first point. ”

Example 1 Use the slope formula to find the slope of each line that passes through the given points. a. (3, 2) and (8, 5) Let (3, 2) be (x 1, y 1) and (8, 5) be (x 2, y 2). Substitute the numbers into the slope formula. Sometimes it helps to write the subscript letters over your points to stay organized: x 1 y 1 x 2 y 2 (3, 2) (8, 5)

Example 1 Continued… Use the slope formula to find the slope of each line that passes through the given points. b. (1, – 1) and (3, – 5) Let (1, – 1) be (x 1, y 1) and (3, – 5) be (x 2, y 2). Substitute the numbers into the slope formula.

Example 1 Continued… Use the slope formula to find the slope of each line that passes through the given points. c. (6, – 2) and (6, 4) Let (6, – 2) be (x 1, y 1) and (6, 4) be (x 2, y 2). Substitute the numbers into the slope formula. It is impossible to divide by 0 so the slope is undefined.

Remember! You have learned three methods for calculating slope. All three methods will work in any situation. Depending on the way the linear relationship is presented, there may be one method that is easier to use than the other two methods. RATE OF CHANGE Easiest method when information is presented in an input-output table. SLOPE TRIANGLE Easiest method when information is presented in a graph. SLOPE FORMULA Easiest method when given two ordered pairs.

Communication Prompt You can find slope from: • A table by finding rate of change. • A graph using a slope triangle. • The slope formula. Which way do you prefer to find slope? Why?

Exit Problems Find the slope of each line that passes through the given points. 1. (4, 0) and (7, 9) 3 2. (9, 2) and (6, 4) 3. (4, − 1) and (4, 3) Undefined