Lesson 2 7 Core Focus on Geometry The

Lesson 2. 7 Core Focus on Geometry The Distance Formula

Warm-Up Find the perimeter of the triangle formed by the points given below. Round to the nearest tenth when necessary. F(7, 1) G(7, 8) H(3, 1) ≈ 19. 1 units

Lesson 2. 7 The Distance Formula Find the distance between two points on a coordinate plane using the Distance Formula.

Vocabulary Distance Formula The formula that allows you to find the distance between any two points on a coordinate plane without graphing first. The vertical leg ofleg theofright horizontal the triangle right is theisdifference between the y-the triangle the difference between coordinates ininthe x-coordinates theorderedpairs. a 2 + b 2 = c 2 (x 2 – x 1)2 + (y 2 – y 1)2 = c 2

The Distance Formula The distance, d, between two points (x 1, y 1) and (x 2, y 2) is found by:

Example 1 Find the distance between (1, 2) and (4, 6). Using the Pythagorean Theorem Using the Distance Formula Let (x 1, y 1) = (1, 2) and (x 2, y 2) = (4, 6). 32 + 42 = c 2 9 + 16 = c 2 25 = c 2 5 = ca The distance between (1, 2) and (4, 6) is 5 units.

Example 2 Find the distance between (0, 8) and (3, 2). Round to the nearest tenth. Write the distance formula. Substitute each value from the ordered pairs into the formula. According to the order of operations, simplify the inside of the parentheses first. Simplify by squaring. Add. Simplify. Round to the nearest tenth. The distance between (3, 2) and (0, 8) is about 6. 7 units.

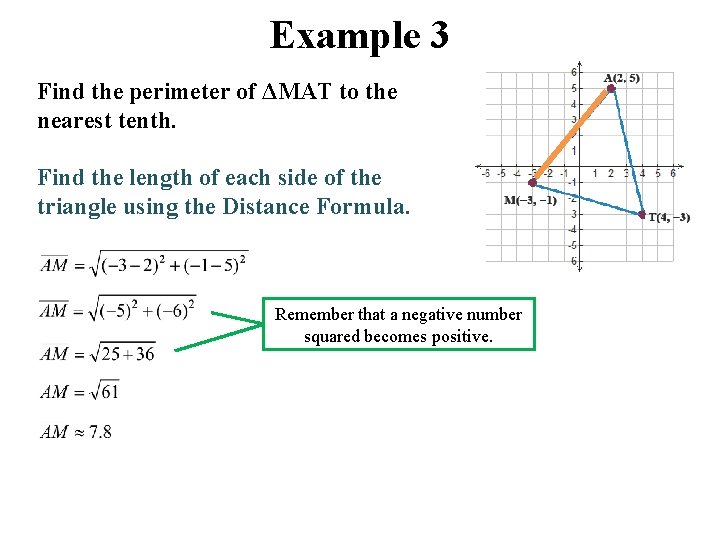
Example 3 Find the perimeter of ΔMAT to the nearest tenth. Find the length of each side of the triangle using the Distance Formula. Remember that a negative number squared becomes positive.

Example 3 Continued… Find the perimeter of ΔMAT to the nearest tenth. Find the length of each side of the triangle using the Distance Formula. The perimeter of ΔMAT is approximately 23. 3 units. Add the lengths of the three sides of the triangle. 7. 8 + 8. 2 + 7. 3 = 23. 3

Communication Prompt When finding the distance between two points, do you prefer using the distance formula or graphing the two points and using the Pythagorean Theorem? Explain your reasoning.

Exit Problems Use the distance formula to find the distance between each pair of points. If necessary, round to the nearest tenth. 1. (2, 7) and (4, 10) ≈ 3. 6 units 2. (− 8, 3) and (7, 11) ≈ 17 units