Lesson 2 4Rotation of Shapes about an Origin

Lesson 2. 4_Rotation of Shapes about an Origin (0, 0)

Homework (12/5/16) Transformational Geometry_Rotations Page 1 and 2

• https: //www. youtube. com/watch? v=VJTxv-t. RKj 0 • http: //www. sciencekids. co. nz/gamesactivities/mat h/transformation. html

Rotation Which of the following are examples of rotation in real life? Opening a door? Walking up stairs? Riding on a Ferris wheel? Bending your arm? Opening your mouth? Opening a drawer? Can you suggest any other examples?

Rotation Vocabulary Rotation – transformation that turns every point of a pre-image through a specified angle and direction about a fixed point. image Pre-image rotation fixed point 6 of 58

A Rotation is an Isometry • Segment lengths are preserved. • Angle measures are preserved. • Parallel lines remain parallel. • Orientation is unchanged. 2/5/2022 7 of 58

Rotation In order to rotate an object we need 3 pieces of information • Center of rotation • Angle of rotation (degrees) • Direction of rotation 8 of 58
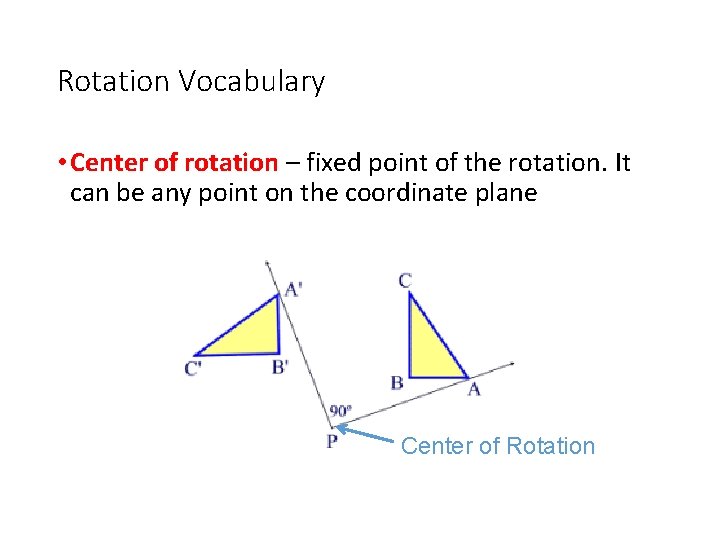
Rotation Vocabulary • Center of rotation – fixed point of the rotation. It can be any point on the coordinate plane Center of Rotation 9 of 58
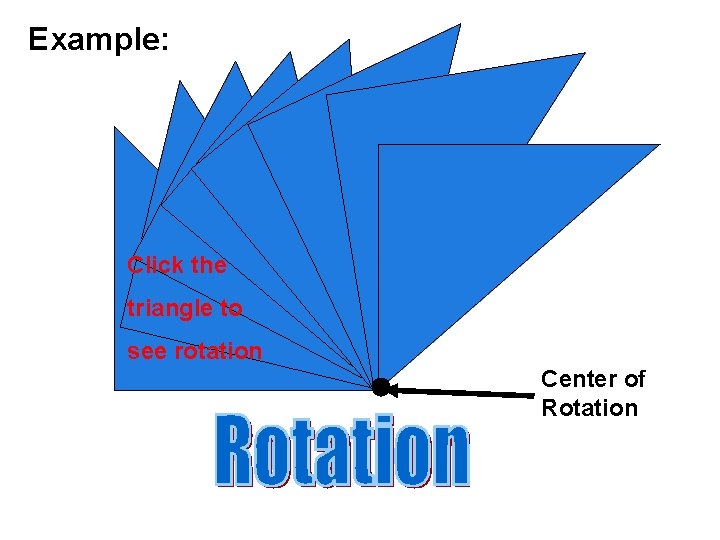
Example: Click the triangle to see rotation Center of Rotation 10 of 58
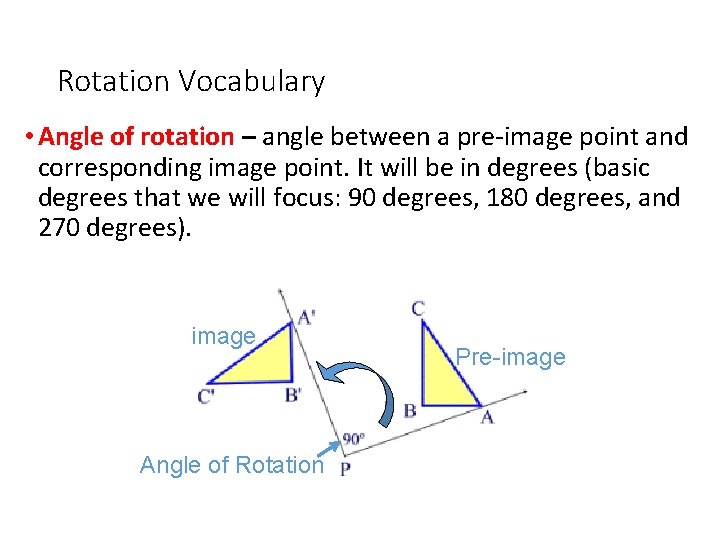
Rotation Vocabulary • Angle of rotation – angle between a pre-image point and corresponding image point. It will be in degrees (basic degrees that we will focus: 90 degrees, 180 degrees, and 270 degrees). image Angle of Rotation 11 of 58 Pre-image
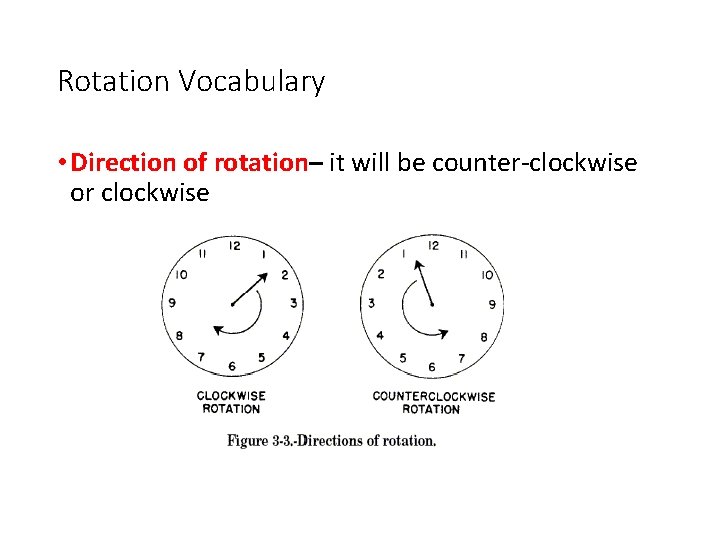
Rotation Vocabulary • Direction of rotation– it will be counter-clockwise or clockwise 12 of 58

Example 1: Identifying Rotations Tell whether each transformation appears to be a rotation. Explain. A. B. No; the figure appears to be flipped. Yes; the figure appears to be turned around a point. 13 of 58
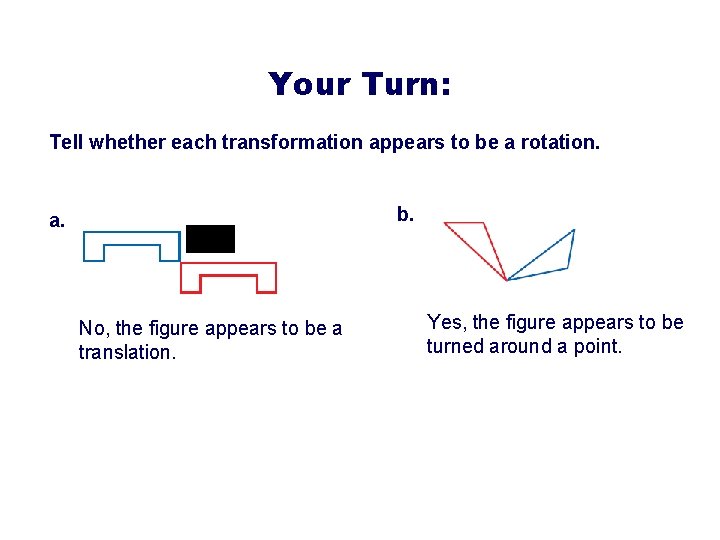
Your Turn: Tell whether each transformation appears to be a rotation. b. a. No, the figure appears to be a translation. 14 of 58 Yes, the figure appears to be turned around a point.
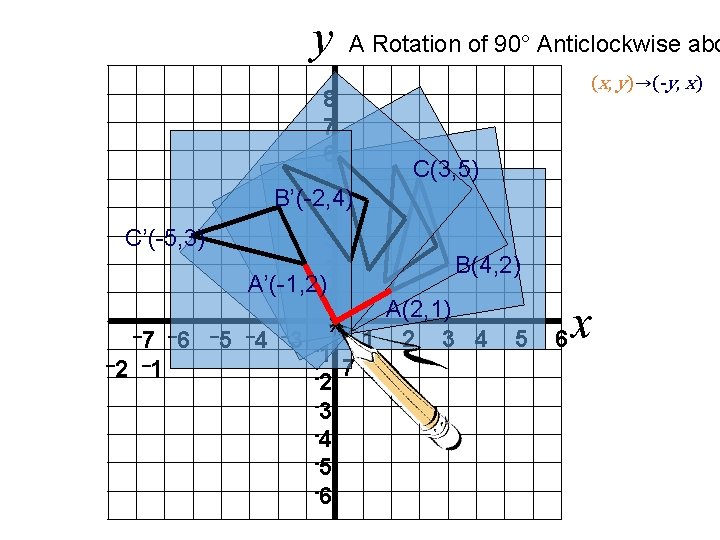
y A Rotation of 90° Anticlockwise abo xx 8 7 6 C(3, 5) 5 B’(-2, 4) 4 C’(-5, 3) 3 B(4, 2) 2 A’(-1, 2) 1 A(2, 1) xx – 7 – 6 – 5 – 4 – 3 1 2 3 4 5 -1 – 2 – 1 -2 7 8 -3 -4 -5 -6 15 of 58 (x, y)→(-y, x) 6 x
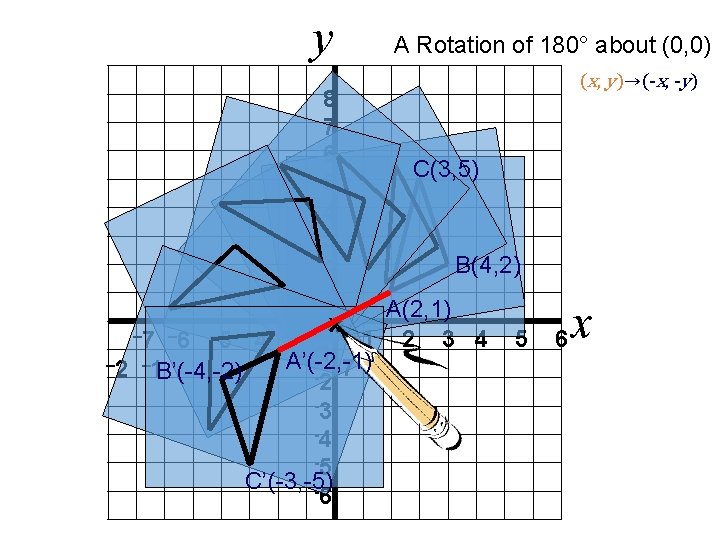
y A Rotation of 180° about (0, 0) 8 7 6 C(3, 5) 5 4 3 B(4, 2) 2 1 A(2, 1) xx – 7 – 6 – 5 – 4 – 3 1 2 3 4 5 -1 A’(-2, -1) – 2 – 1 B’(-4, -2) -2 7 8 -3 -4 -5 C’(-3, -5) -6 xxx xx 16 of 58 (x, y)→(-x, -y) 6 x
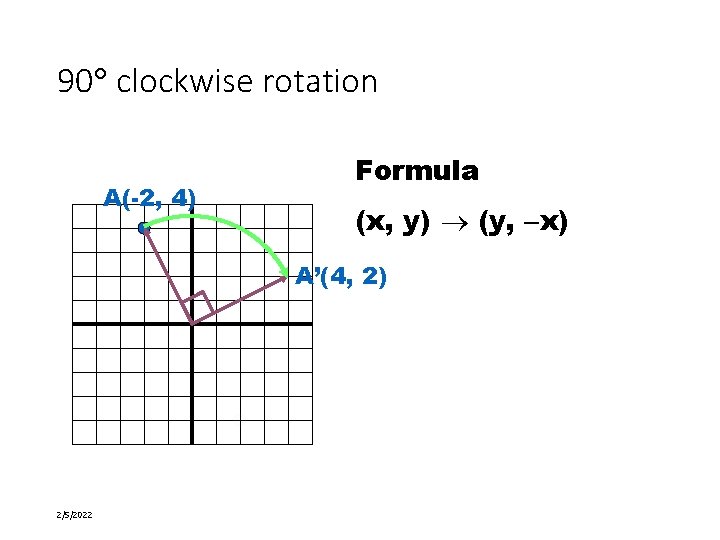
90 clockwise rotation A(-2, 4) Formula (x, y) (y, x) A’(4, 2) 2/5/2022 17 of 58
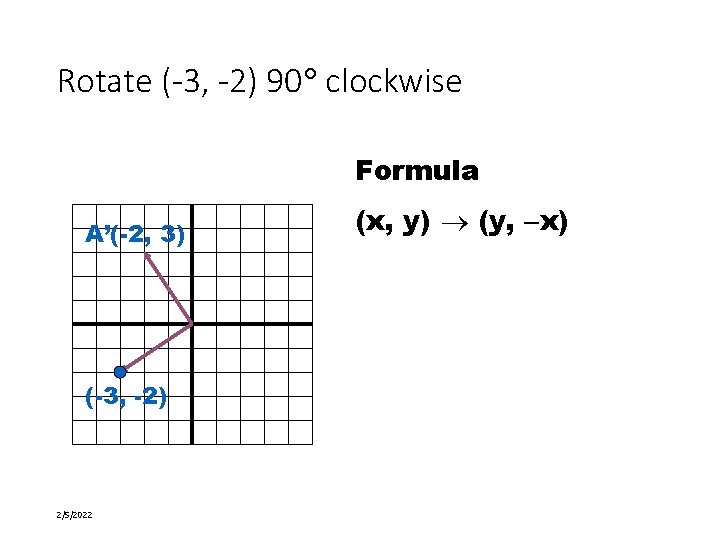
Rotate (-3, -2) 90 clockwise Formula A’(-2, 3) (-3, -2) 2/5/2022 18 of 58 (x, y) (y, x)
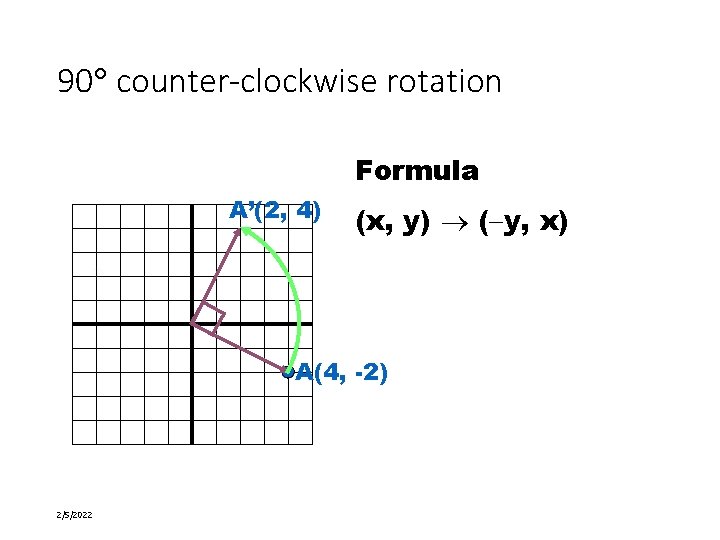
90 counter-clockwise rotation Formula A’(2, 4) (x, y) ( y, x) A(4, -2) 2/5/2022 19 of 58
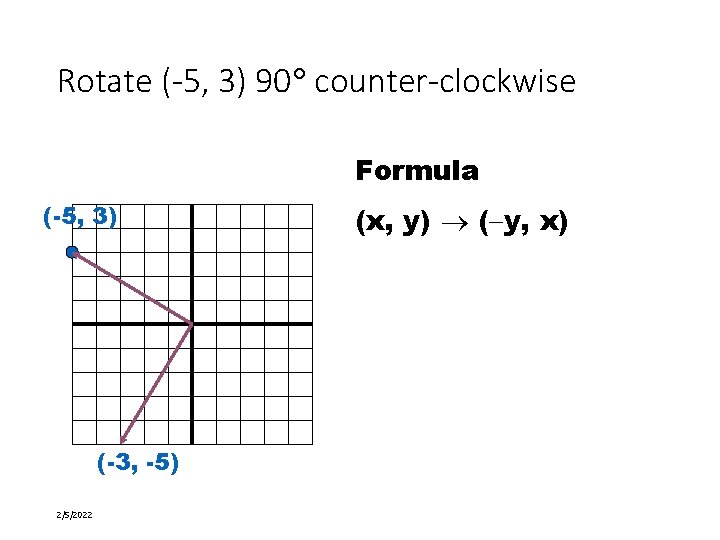
Rotate (-5, 3) 90 counter-clockwise Formula (-5, 3) (-3, -5) 2/5/2022 20 of 58 (x, y) ( y, x)
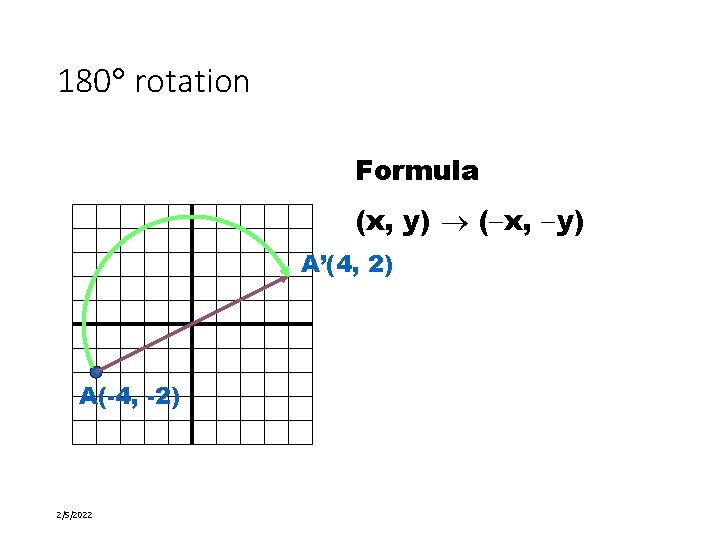
180 rotation Formula (x, y) ( x, y) A’(4, 2) A(-4, -2) 2/5/2022 21 of 58
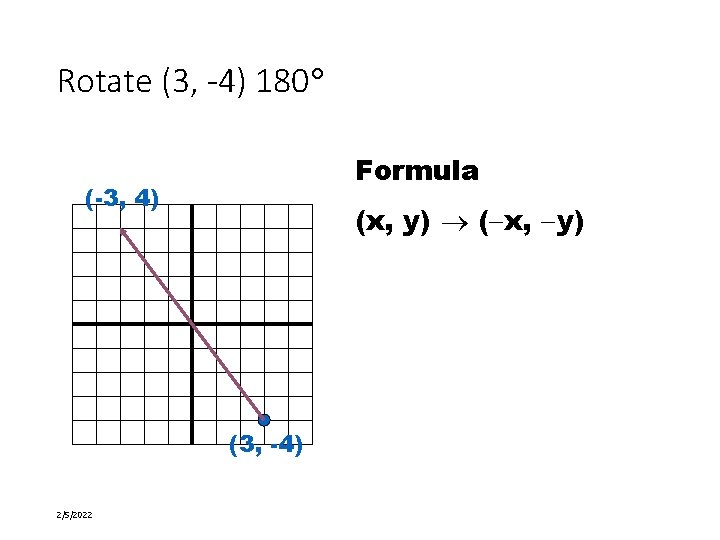
Rotate (3, -4) 180 Formula (-3, 4) (x, y) ( x, y) (3, -4) 2/5/2022 22 of 58
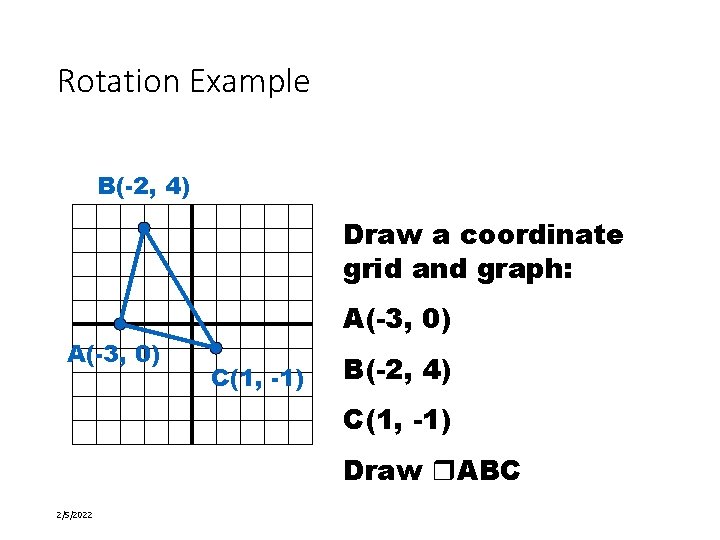
Rotation Example B(-2, 4) Draw a coordinate grid and graph: A(-3, 0) C(1, -1) B(-2, 4) C(1, -1) Draw ABC 2/5/2022 23 of 58
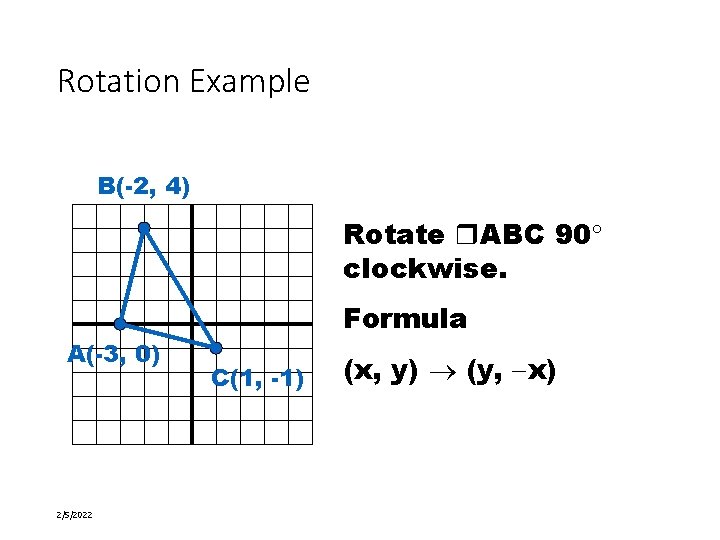
Rotation Example B(-2, 4) Rotate ABC 90 clockwise. A(-3, 0) 2/5/2022 24 of 58 Formula C(1, -1) (x, y) (y, x)
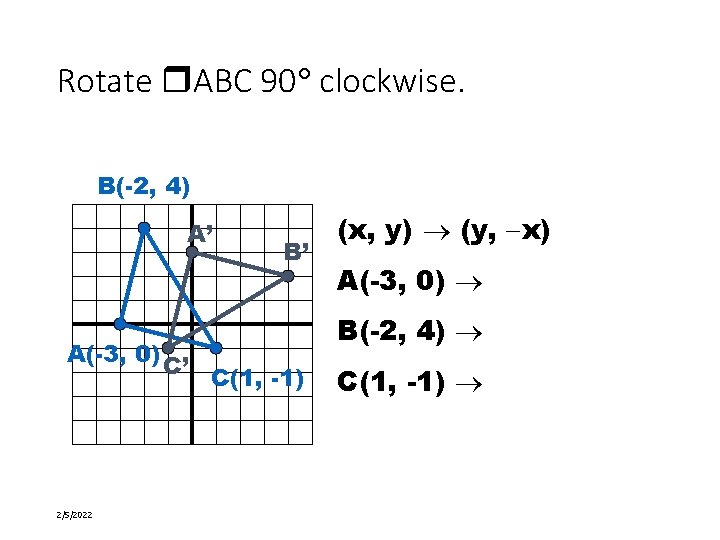
Rotate ABC 90 clockwise. B(-2, 4) A’ B’ A(-3, 0) C’ C(1, -1) 2/5/2022 25 of 58 (x, y) (y, x) A(-3, 0) A’(0, 3) B(-2, 4) B’(4, 2) C(1, -1) C’(-1, -1)
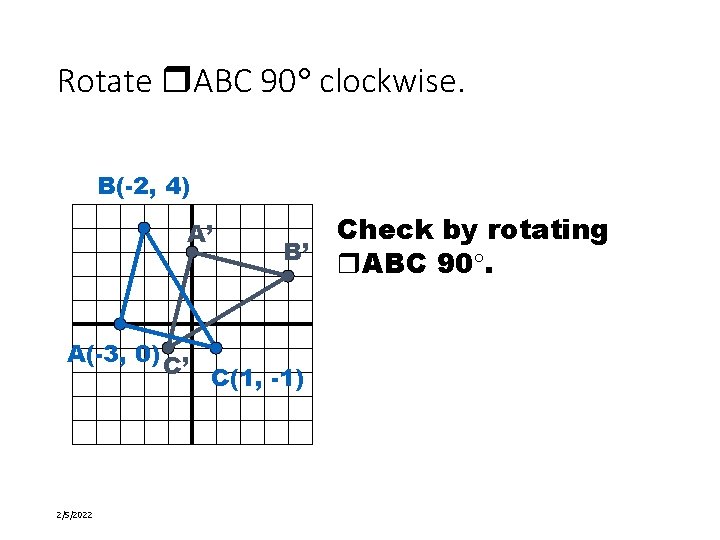
Rotate ABC 90 clockwise. B(-2, 4) A’ B’ A(-3, 0) C’ C(1, -1) 2/5/2022 26 of 58 Check by rotating ABC 90.

Rotation in a Coordinate Plane 27 of 58

Checkpoint Rotations in a Coordinate Plane 4. Sketch the triangle with vertices A(0, 0), B(3, 0), and C(3, 4). Rotate ∆ABC 90° counterclockwise about the origin. Name the coordinates of the new vertices A', B', and C'. ANSWER A'(0, 0), B'(0, 3), C'(– 4, 3) 28 of 58
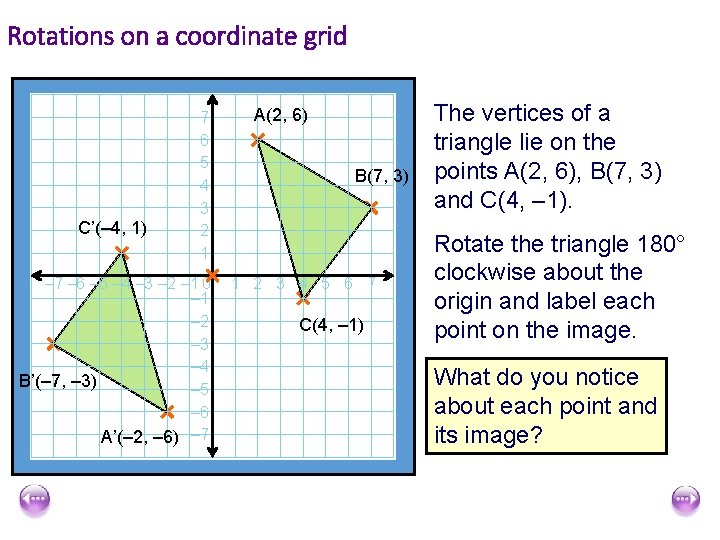
Rotations on a coordinate grid C’(– 4, 1) 7 6 5 4 3 2 1 – 7 – 6 – 5 – 4 – 3 – 2 – 1 0 – 1 – 2 – 3 – 4 B’(– 7, – 3) – 5 – 6 A’(– 2, – 6) – 7 A(2, 6) B(7, 3) 1 2 3 4 5 6 7 C(4, – 1) The vertices of a triangle lie on the points A(2, 6), B(7, 3) and C(4, – 1). Rotate the triangle 180° clockwise about the origin and label each point on the image. What do you notice about each point and its image?
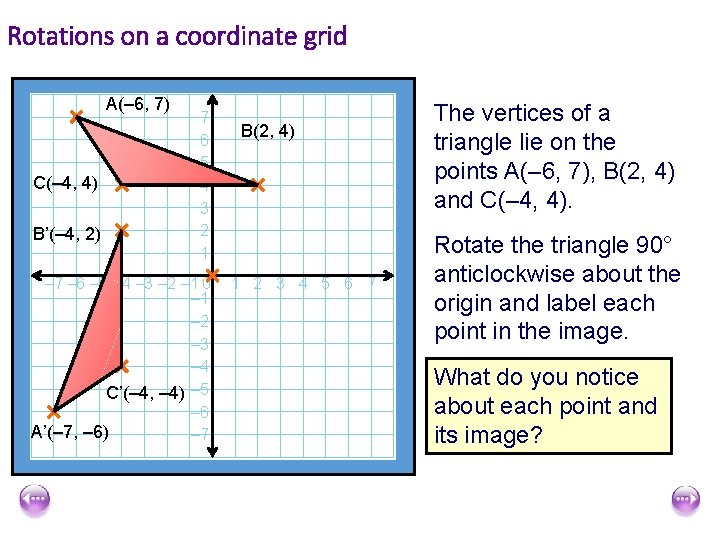
Rotations on a coordinate grid A(– 6, 7) C(– 4, 4) B’(– 4, 2) 7 6 5 4 3 2 1 – 7 – 6 – 5 – 4 – 3 – 2 – 1 0 – 1 – 2 – 3 – 4 C’(– 4, – 4) – 5 – 6 A’(– 7, – 6) – 7 B(2, 4) 1 2 3 4 5 6 7 The vertices of a triangle lie on the points A(– 6, 7), B(2, 4) and C(– 4, 4). Rotate the triangle 90° anticlockwise about the origin and label each point in the image. What do you notice about each point and its image?
- Slides: 30